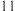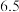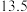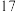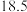名校
1 . 请阅读:在等式 (
( )的两边对
)的两边对 求导得
求导得
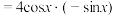 ,化简后得等式
,化简后得等式 .
.
请类比上述方法,试由等式 (
( ,
,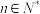 且
且 ).
).
(1)证明: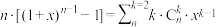 (注:
(注: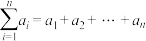 );
);
(2)求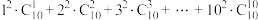 .
.
 (
( )的两边对
)的两边对 求导得
求导得
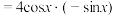 ,化简后得等式
,化简后得等式 .
.请类比上述方法,试由等式
 (
( ,
,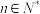 且
且 ).
).(1)证明:
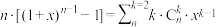 (注:
(注: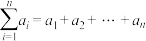 );
);(2)求
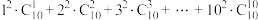 .
.
您最近一年使用:0次
12-13高三上·江苏盐城·阶段练习
名校
解题方法
2 . 已知 ,(其中
,(其中 ).
).
(1)求 及
及 ;
;
(2)试比较 与
与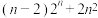 的大小,并用数学归纳法给出证明过程.
的大小,并用数学归纳法给出证明过程.
 ,(其中
,(其中 ).
).(1)求
 及
及 ;
;(2)试比较
 与
与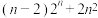 的大小,并用数学归纳法给出证明过程.
的大小,并用数学归纳法给出证明过程.
您最近一年使用:0次
2017-05-17更新
|
1112次组卷
|
7卷引用:2012届江苏省阜宁中学高三第一学期第二次阶段考试数学
(已下线)2012届江苏省阜宁中学高三第一学期第二次阶段考试数学(已下线)2013-2014学年江苏省扬州中学高二下学期月考数学试卷2014-2015学年河南实验中学高二下学期期中理科数学试卷辽宁省葫芦岛市第一高级中学2016-2017学年高二下学期期中考试数学(理)试题【全国百强校】安徽省蚌埠市第二中学2018-2019学年高二下学期期中考试数学(理)试题河南省八市2018-2019学年高二下学期第二次质量检测数学(理)(已下线)专题1 数学归纳法及其变种 微点1 数学归纳法
名校
3 . 设f(n)=(a+b)n(n∈N*,n≥2),若f(n)的展开式中,存在某连续3项,其二项式系数依次成等差数列,则称f(n)具有性质P.
(1)求证:f(7)具有性质P;
(2)若存在n≤2016,使f(n)具有性质P,求n的最大值.
(1)求证:f(7)具有性质P;
(2)若存在n≤2016,使f(n)具有性质P,求n的最大值.
您最近一年使用:0次
2016-12-04更新
|
1748次组卷
|
4卷引用:2016届江苏省南京市高三第三次学情调研测试数学试卷
2016届江苏省南京市高三第三次学情调研测试数学试卷(已下线)专题15+计数原理与二项式定理-2021高考数学(理)高频考点、热点题型归类强化河南省信阳市2020-2021学年高二下学期期末数学(理)试题辽宁省朝阳市建平县实验中学2022-2023学年高二下学期4月月考数学试题
2014·全国·一模
解题方法
4 . 如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
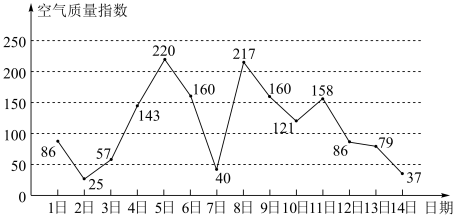
(1)求3月1日到14日空气质量指数的中位数;
(2)求此人到达当日空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)

(1)求3月1日到14日空气质量指数的中位数;
(2)求此人到达当日空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
您最近一年使用:0次
2016-12-03更新
|
1495次组卷
|
3卷引用:2014年高考数学三轮冲刺模拟 概率与统计
5 . 中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的从高气温,下面的折线代表可能出现的最低气温.
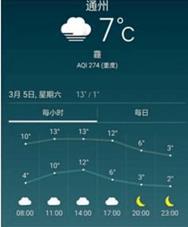
(Ⅰ)指出最高气温与最低气温的相关性;
(Ⅱ)估计在10:00时最高气温和最低气温的差;
(Ⅲ)比较最低气温与最高气温方差的大小(结论不要求证明).

(Ⅰ)指出最高气温与最低气温的相关性;
(Ⅱ)估计在10:00时最高气温和最低气温的差;
(Ⅲ)比较最低气温与最高气温方差的大小(结论不要求证明).
您最近一年使用:0次
2016-12-04更新
|
374次组卷
|
2卷引用:2016届北京通州区高三4月一模数学(文)试卷
6 . (1)求证: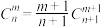 ;
;
(2)求和: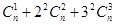
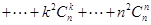 .
.
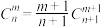 ;
;(2)求和:
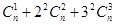
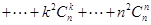 .
.
您最近一年使用:0次
7 . 已知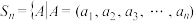 ,
,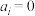 或1,
或1,
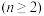 ,对于
,对于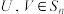 ,
,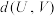 表示U和V中相对应的元素不同的个数.
表示U和V中相对应的元素不同的个数.
(Ⅰ)令 ,存在m个
,存在m个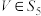 ,使得
,使得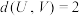 ,写出m的值;
,写出m的值;
(Ⅱ)令 ,若
,若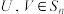 ,求证:
,求证: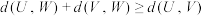 ;
;
(Ⅲ)令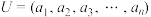 ,若
,若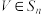 ,求所有
,求所有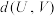 之和.
之和.
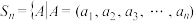 ,
,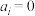 或1,
或1,
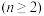 ,对于
,对于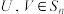 ,
,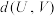 表示U和V中相对应的元素不同的个数.
表示U和V中相对应的元素不同的个数.(Ⅰ)令
 ,存在m个
,存在m个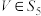 ,使得
,使得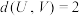 ,写出m的值;
,写出m的值;(Ⅱ)令
 ,若
,若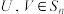 ,求证:
,求证: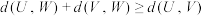 ;
;(Ⅲ)令
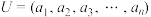 ,若
,若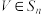 ,求所有
,求所有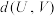 之和.
之和.
您最近一年使用:0次
2016-11-30更新
|
772次组卷
|
6卷引用:2011届北京市丰台区高三下学期统一练习数学理卷
(已下线)2011届北京市丰台区高三下学期统一练习数学理卷(已下线)2013届中国人民大学附属中学高考冲刺五理科数学试卷2015届北京市第四中学高三上学期期中考试理科数学试卷北京市京源学校2017-2018学年高三十月月考数学试题(已下线)上海市华东师范大学第二附属中学2022-2023学年高一上学期开学考试数学试题(已下线)第6章 计数原理(基础、常考、易错、压轴)分类专项训练-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)
8 . 某学校高一 、高二 、高三三个年级共有  名教师,为调查他们的备课时间情况,通过分层
名教师,为调查他们的备课时间情况,通过分层
抽样获得了 名教师一周的备课时间 ,数据如下表(单位 :小时):
名教师一周的备课时间 ,数据如下表(单位 :小时):
(1)试估计该校高三年级的教师人数 ;
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲 ,高二年级选出的人记为乙 ,求该周甲的备课时间不比乙的备课时间长的概率 ;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是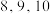 (单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为
(单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为 ,表格中的数据平均数记为
,表格中的数据平均数记为 ,试判断
,试判断 与
与 的大小. (结论不要求证明)
的大小. (结论不要求证明)
 名教师,为调查他们的备课时间情况,通过分层
名教师,为调查他们的备课时间情况,通过分层抽样获得了
 名教师一周的备课时间 ,数据如下表(单位 :小时):
名教师一周的备课时间 ,数据如下表(单位 :小时):高一年级 |
|
|
|
|
| |||
高二年级 |
|
|
|
|
|
|
| |
高三年级 |
|
|
|
|
|
|
|
|
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲 ,高二年级选出的人记为乙 ,求该周甲的备课时间不比乙的备课时间长的概率 ;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是
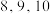 (单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为
(单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为 ,表格中的数据平均数记为
,表格中的数据平均数记为 ,试判断
,试判断 与
与 的大小. (结论不要求证明)
的大小. (结论不要求证明)
您最近一年使用:0次
2017-04-02更新
|
774次组卷
|
8卷引用:2017届安徽省蚌埠市第二次(3月)教学质量检查数学(文)试卷
解题方法
9 . 数学运算中,常用符号来表示算式,如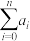 =
=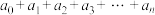 ,其中
,其中 ,
, .
.
(Ⅰ)若 ,
, ,
, ,…,
,…, 成等差数列,且
成等差数列,且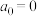 ,公差
,公差 ,求证:
,求证: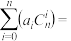
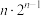 ;
;
(Ⅱ)若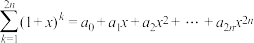 ,
, ,记
,记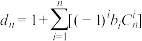 ,且不等式
,且不等式 对于
对于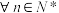 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
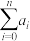 =
=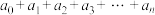 ,其中
,其中 ,
, .
.(Ⅰ)若
 ,
, ,
, ,…,
,…, 成等差数列,且
成等差数列,且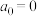 ,公差
,公差 ,求证:
,求证: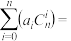
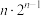 ;
;(Ⅱ)若
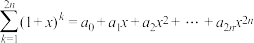 ,
, ,记
,记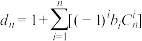 ,且不等式
,且不等式 对于
对于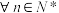 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2016-12-03更新
|
1615次组卷
|
5卷引用:2015届江苏高考南通密卷三数学试卷
10 . 为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测.检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3) 现从A班的上述5名学生中随机选取3名学生,用X表示其中视力大于4.6的人数,求X的分布列和数学期望.
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3) 现从A班的上述5名学生中随机选取3名学生,用X表示其中视力大于4.6的人数,求X的分布列和数学期望.
您最近一年使用:0次