1 . 已知函数 .
.
(1)求函数 的极大值点;
的极大值点;
(2)若 为函数
为函数 的极大值点,证明:存在
的极大值点,证明:存在 使
使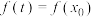 且
且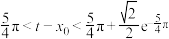 .
.
 .
.(1)求函数
 的极大值点;
的极大值点;(2)若
 为函数
为函数 的极大值点,证明:存在
的极大值点,证明:存在 使
使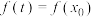 且
且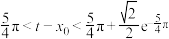 .
.
您最近一年使用:0次
2 . 已知函数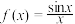 .
.
(1)这比较 与
与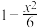 的大小;
的大小;
(2)求证:当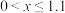 时,
时, .参考数据:
.参考数据: .
.
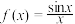 .
.(1)这比较
 与
与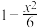 的大小;
的大小;(2)求证:当
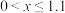 时,
时, .参考数据:
.参考数据: .
.
您最近一年使用:0次
2022-11-24更新
|
251次组卷
|
2卷引用:山东省青岛市莱西市2022-2023学年高三上学期期中数学试题
名校
3 . 已知函数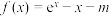 (
( ),
),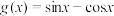 (
( ),则下列说法正确的是( )
),则下列说法正确的是( )
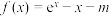 (
( ),
),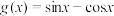 (
( ),则下列说法正确的是( )
),则下列说法正确的是( )A.若 有两个零点,则 有两个零点,则 |
B.若 且 且 ,则 ,则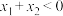 |
C.函数 在区间 在区间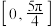 有两个极值点 有两个极值点 |
D.过原点的动直线l与曲线 相切,切点的横坐标从小到大依次为: 相切,切点的横坐标从小到大依次为: , , ,…, ,…, .则 .则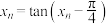 |
您最近一年使用:0次
2022-11-18更新
|
689次组卷
|
4卷引用:湖北省高中名校联盟2023届高三上学期第二次联合测评数学试题
4 . 下列判断正确的有( )
A.当 时,方程 时,方程 存在唯一实数解 存在唯一实数解 |
B.当 时, 时,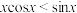 |
C.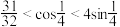 |
D. |
您最近一年使用:0次
名校
5 . 已知函数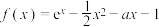 ,若
,若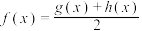 ,其中
,其中 为偶函数,
为偶函数, 为奇函数.
为奇函数.
(1)当 时,求出函数
时,求出函数 的表达式并讨论函数
的表达式并讨论函数 的单调性;
的单调性;
(2)设 是
是 的导数. 当
的导数. 当 ,
, 时,记函数
时,记函数 的最大值为
的最大值为 ,函数
,函数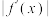 的最大值为
的最大值为 .求证:
.求证: .
.
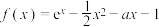 ,若
,若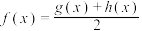 ,其中
,其中 为偶函数,
为偶函数, 为奇函数.
为奇函数.(1)当
 时,求出函数
时,求出函数 的表达式并讨论函数
的表达式并讨论函数 的单调性;
的单调性;(2)设
 是
是 的导数. 当
的导数. 当 ,
, 时,记函数
时,记函数 的最大值为
的最大值为 ,函数
,函数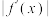 的最大值为
的最大值为 .求证:
.求证: .
.
您最近一年使用:0次
2022-11-04更新
|
311次组卷
|
3卷引用:河南省南阳市2022-2023学年高三上学期期中数学理科试题
河南省南阳市2022-2023学年高三上学期期中数学理科试题河南省顶级名校2022-2023学年高三上学期1月阶段性检测理科数学试题(已下线)河南省济源市、平顶山市、许昌市2022届高三文科数学试题变式题21-23
6 . 已知函数 ,其中
,其中 为自然对数的底数,
为自然对数的底数,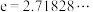
(1)若对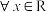 ,
, 恒成立,求实数
恒成立,求实数 的值;
的值;
(2)在(1)的条件下,
(i)证明: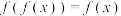 有三个根
有三个根 ;
;
(ii)设 ,请从以下不等式中任选一个进行证明:
,请从以下不等式中任选一个进行证明:
①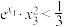 ;②
;②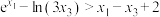 .
.
参考数据: ,
, ,
,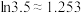
 ,其中
,其中 为自然对数的底数,
为自然对数的底数,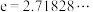
(1)若对
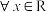 ,
, 恒成立,求实数
恒成立,求实数 的值;
的值;(2)在(1)的条件下,
(i)证明:
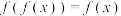 有三个根
有三个根 ;
;(ii)设
 ,请从以下不等式中任选一个进行证明:
,请从以下不等式中任选一个进行证明:①
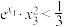 ;②
;②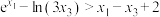 .
.参考数据:
 ,
, ,
,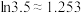
您最近一年使用:0次
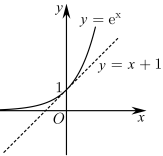
7 . “切线放缩”是处理不等式问题的一种技巧.如: 在点
在点 处的切线为
处的切线为 ,如图所示,易知除切点
,如图所示,易知除切点 外,
外, 图象上其余所有的点均在
图象上其余所有的点均在 的上方,故有
的上方,故有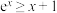 .该结论可构造函数
.该结论可构造函数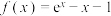 并求其最小值来证明.显然,我们选择的切点不同,所得的不等式也不同.请根据以上材料,判断下列命题中正确的命题是( )
并求其最小值来证明.显然,我们选择的切点不同,所得的不等式也不同.请根据以上材料,判断下列命题中正确的命题是( )
 在点
在点 处的切线为
处的切线为 ,如图所示,易知除切点
,如图所示,易知除切点 外,
外, 图象上其余所有的点均在
图象上其余所有的点均在 的上方,故有
的上方,故有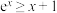 .该结论可构造函数
.该结论可构造函数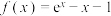 并求其最小值来证明.显然,我们选择的切点不同,所得的不等式也不同.请根据以上材料,判断下列命题中正确的命题是( )
并求其最小值来证明.显然,我们选择的切点不同,所得的不等式也不同.请根据以上材料,判断下列命题中正确的命题是( )
A.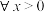 , , | B. , , , ,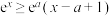 |
C. , ,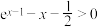 | D.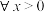 , , |
您最近一年使用:0次
2022-05-31更新
|
1071次组卷
|
6卷引用:广东省东莞实验中学2022-2023学年高二下学期期中数学试题
广东省东莞实验中学2022-2023学年高二下学期期中数学试题重庆市第十一中学校2021-2022学年高二下学期5月质量抽测数学试题(已下线)第16讲:第三章 一元函数的导数及其应用(测)(中档卷)-2023年高考数学一轮复习讲练测(新教材新高考)(已下线)第16讲:第三章 一元函数的导数及其应用(测)(中档卷)-2023年高考数学一轮复习讲练测(新教材新高考)福建省莆田第一中学2021-2022学年高二下学期数学期末模拟试题(1)山东省滕州市第一中学2022-2023学年高二下学期3月质量检测数学试题
名校
8 . 关于 的函数
的函数 ,我们曾在必修一中学习过“二分法”求其零点近似值.现结合导函数,介绍另一种求零点近似值的方法——“牛顿切线法”.
,我们曾在必修一中学习过“二分法”求其零点近似值.现结合导函数,介绍另一种求零点近似值的方法——“牛顿切线法”.
(1)证明: 有唯一零点
有唯一零点 ,且
,且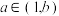 ;
;
(2)现在,我们任取 (1,a)开始,实施如下步骤:
(1,a)开始,实施如下步骤:
在 处作曲线
处作曲线 的切线,交
的切线,交 轴于点
轴于点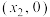 ;
;
在 处作曲线
处作曲线 的切线,交
的切线,交 轴于点
轴于点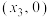 ;
;
……
在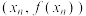 处作曲线
处作曲线 的切线,交
的切线,交 轴于点
轴于点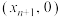 ;
;
可以得到一个数列 ,它的各项都是
,它的各项都是 不同程度的零点近似值.
不同程度的零点近似值.
(i)设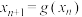 ,求
,求 的解析式(用
的解析式(用 表示
表示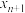 );
);
(ii)证明:当 ,总有
,总有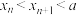 .
.
 的函数
的函数 ,我们曾在必修一中学习过“二分法”求其零点近似值.现结合导函数,介绍另一种求零点近似值的方法——“牛顿切线法”.
,我们曾在必修一中学习过“二分法”求其零点近似值.现结合导函数,介绍另一种求零点近似值的方法——“牛顿切线法”.(1)证明:
 有唯一零点
有唯一零点 ,且
,且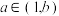 ;
;(2)现在,我们任取
 (1,a)开始,实施如下步骤:
(1,a)开始,实施如下步骤:在
 处作曲线
处作曲线 的切线,交
的切线,交 轴于点
轴于点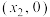 ;
; 在
 处作曲线
处作曲线 的切线,交
的切线,交 轴于点
轴于点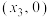 ;
;……
在
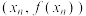 处作曲线
处作曲线 的切线,交
的切线,交 轴于点
轴于点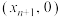 ;
;可以得到一个数列
 ,它的各项都是
,它的各项都是 不同程度的零点近似值.
不同程度的零点近似值.(i)设
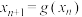 ,求
,求 的解析式(用
的解析式(用 表示
表示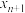 );
); (ii)证明:当
 ,总有
,总有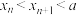 .
.
您最近一年使用:0次
2022-05-27更新
|
1632次组卷
|
8卷引用:四川省眉山市青神县青神中学校2023-2024学年高二下学期4月期中考试数学试题
四川省眉山市青神县青神中学校2023-2024学年高二下学期4月期中考试数学试题广东省八校(石门中学、国华纪念中学、三水中学、珠海一中、中山纪念中学、湛江一中、河源中学、深圳实验学校)2021-2022学年高二下学期5月联考数学试题(已下线)专题08 证明不等式问题22024年普通高等学校招生全国统一考试数学模拟试题(二)(新高考九省联考题型)重庆市杨家坪中学2023-2024学年高三下学期第二次月考数学试题 (已下线)第6套 重组模拟卷(模块二 2月开学)重庆市九龙坡区渝高中学校2023-2024学年高二下学期第一次月考数学试题2024届福建省泉州市四校(安溪一中、养正中学、惠安一中、泉州实验中学)5月份高三高考模拟联考数学试题
名校
解题方法
9 . 对于正实数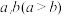 有基本不等式:
有基本不等式: ,其中
,其中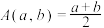 ,为
,为 的算术平均数,
的算术平均数,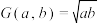 ,为
,为 的几何平均数.现定义
的几何平均数.现定义 的对数平均数:
的对数平均数:
(1)设 ,求证:
,求证: :
:
(2)①证明不等式: :
:
②若不等式 对于任意的正实数
对于任意的正实数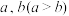 恒成立,求正实数
恒成立,求正实数 的最大值.
的最大值.
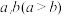 有基本不等式:
有基本不等式: ,其中
,其中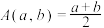 ,为
,为 的算术平均数,
的算术平均数,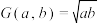 ,为
,为 的几何平均数.现定义
的几何平均数.现定义 的对数平均数:
的对数平均数:
(1)设
 ,求证:
,求证: :
:(2)①证明不等式:
 :
:②若不等式
 对于任意的正实数
对于任意的正实数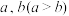 恒成立,求正实数
恒成立,求正实数 的最大值.
的最大值.
您最近一年使用:0次
2022-05-11更新
|
596次组卷
|
7卷引用:湖南省长沙市明德中学2021-2022学年高二下学期期中数学试题
名校
解题方法
10 . 已知函数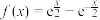
(1)若不等式 对任意的
对任意的 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)设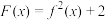 ,若数列
,若数列 满足
满足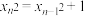 ,其中
,其中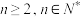 ,当
,当 时,证明:
时,证明: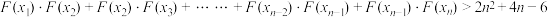
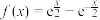
(1)若不等式
 对任意的
对任意的 恒成立,求
恒成立,求 的取值范围;
的取值范围;(2)设
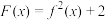 ,若数列
,若数列 满足
满足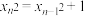 ,其中
,其中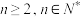 ,当
,当 时,证明:
时,证明: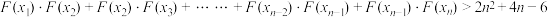
您最近一年使用:0次



