解题方法
1 . 已知: 是平面
是平面 的斜线,斜足为点
的斜线,斜足为点 ,
,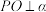 ,垂足为点
,垂足为点 ,直线
,直线 是
是 在平面
在平面 上的投影.
上的投影.
①若空间任一直线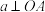 ,则
,则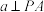 ;②若空间任一直线
;②若空间任一直线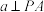 ,则
,则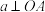 ;③若平面
;③若平面 上的任一直线
上的任一直线 ,
,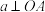 ,则
,则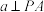 ;④若平面
;④若平面 上的任一直线
上的任一直线 ,
,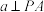 ,则
,则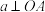 .
.
其中正确的命题序号为________ .
 是平面
是平面 的斜线,斜足为点
的斜线,斜足为点 ,
,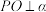 ,垂足为点
,垂足为点 ,直线
,直线 是
是 在平面
在平面 上的投影.
上的投影.①若空间任一直线
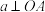 ,则
,则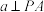 ;②若空间任一直线
;②若空间任一直线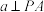 ,则
,则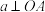 ;③若平面
;③若平面 上的任一直线
上的任一直线 ,
,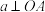 ,则
,则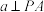 ;④若平面
;④若平面 上的任一直线
上的任一直线 ,
,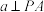 ,则
,则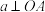 .
.其中正确的命题序号为
您最近一年使用:0次
2024-08-02更新
|
105次组卷
|
2卷引用:【课后练】10.3.4三垂线定理 课后作业-沪教版(2020)必修第三册第10章 空间直线与平面
24-25高二·上海·假期作业
解题方法
2 . 证明:在正三棱锥中,任意两条异面的棱都相互垂直.
您最近一年使用:0次
名校
解题方法
3 . 在长方体 中,
中, ,
,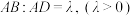 ,
, 是棱
是棱 的中点,点
的中点,点 是线段
是线段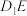 上的动点,给出以下两个命题:①无论
上的动点,给出以下两个命题:①无论 取何值,都存在点
取何值,都存在点 ,使得
,使得 ;②无论
;②无论 取何值,都不存在点
取何值,都不存在点 ,使得直线
,使得直线 平面
平面 .则( ).
.则( ).
 中,
中, ,
,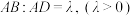 ,
, 是棱
是棱 的中点,点
的中点,点 是线段
是线段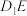 上的动点,给出以下两个命题:①无论
上的动点,给出以下两个命题:①无论 取何值,都存在点
取何值,都存在点 ,使得
,使得 ;②无论
;②无论 取何值,都不存在点
取何值,都不存在点 ,使得直线
,使得直线 平面
平面 .则( ).
.则( ).| A.①成立,②成立 | B.①成立,②不成立 |
| C.①不成立,②成立 | D.①不成立,②不成立 |
您最近一年使用:0次
名校
解题方法
4 . 给定下列四个命题:
①图像不经过点 的幂函数一定不是偶函数;
的幂函数一定不是偶函数;
②若一条直线垂直于平面内的无穷多条直线,则这条直线垂直于这个平面;
③有两个相邻的侧面是矩形的棱柱是直棱柱;
④设数列 的前
的前 项和为
项和为 ,若
,若 是递增数列,则数列
是递增数列,则数列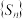 也是递增数列;
也是递增数列;
以上命题是真命题的序号是( )
①图像不经过点
 的幂函数一定不是偶函数;
的幂函数一定不是偶函数;②若一条直线垂直于平面内的无穷多条直线,则这条直线垂直于这个平面;
③有两个相邻的侧面是矩形的棱柱是直棱柱;
④设数列
 的前
的前 项和为
项和为 ,若
,若 是递增数列,则数列
是递增数列,则数列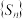 也是递增数列;
也是递增数列;以上命题是真命题的序号是( )
| A.①② | B.②③ |
| C.③④ | D.①③ |
您最近一年使用:0次
2023-02-07更新
|
231次组卷
|
3卷引用:上海市延安中学2022届高三上学期期中数学试题
名校
解题方法
5 . 已知 是两个不同平面,
是两个不同平面, 是两条不同直线,下列命题中:①“直线
是两条不同直线,下列命题中:①“直线 、
、 为异面直线”的充分非必要条件是“直线
为异面直线”的充分非必要条件是“直线 、
、 不相交”; ②垂直于三角形两边的直线必垂直第三边;③
不相交”; ②垂直于三角形两边的直线必垂直第三边;③ 内有不共线三点到
内有不共线三点到 距离相等,则
距离相等,则

 ;④若直线
;④若直线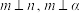 ,则
,则

 ; ⑤若
; ⑤若

 ,
, ,则
,则 ;⑥若
;⑥若 ,则
,则

 ,其中正确的命题编号为
,其中正确的命题编号为________ .
 是两个不同平面,
是两个不同平面, 是两条不同直线,下列命题中:①“直线
是两条不同直线,下列命题中:①“直线 、
、 为异面直线”的充分非必要条件是“直线
为异面直线”的充分非必要条件是“直线 、
、 不相交”; ②垂直于三角形两边的直线必垂直第三边;③
不相交”; ②垂直于三角形两边的直线必垂直第三边;③ 内有不共线三点到
内有不共线三点到 距离相等,则
距离相等,则

 ;④若直线
;④若直线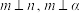 ,则
,则

 ; ⑤若
; ⑤若

 ,
, ,则
,则 ;⑥若
;⑥若 ,则
,则

 ,其中正确的命题编号为
,其中正确的命题编号为
您最近一年使用:0次
名校
6 . 如图,在直角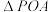 中,PO⊥OA,PO=2OA,将
中,PO⊥OA,PO=2OA,将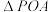 绕边PO旋转到
绕边PO旋转到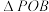 的位置,使
的位置,使 ,得到圆锥的一部分,点C为
,得到圆锥的一部分,点C为 的中点.
的中点. ;
;
(2)设直线PC与平面PAB所成的角为 ,求
,求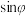 .
.
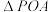 中,PO⊥OA,PO=2OA,将
中,PO⊥OA,PO=2OA,将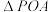 绕边PO旋转到
绕边PO旋转到 的位置,使
的位置,使 ,得到圆锥的一部分,点C为
,得到圆锥的一部分,点C为 的中点.
的中点.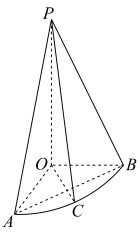
 ;
;(2)设直线PC与平面PAB所成的角为
 ,求
,求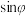 .
.
您最近一年使用:0次
2022-05-12更新
|
1770次组卷
|
14卷引用:上海市华东师范大学第二附属中学2023届高三上学期10月月考数学试题
(已下线)上海市华东师范大学第二附属中学2023届高三上学期10月月考数学试题上海市洋泾中学2022-2023学年高二上学期期中数学试题(已下线)重难点01 空间角度和距离五种解题方法【课后练】3.4.3.1求角的大小 课后作业-沪教版(2020)选择性必修第一册 第3章 空间向量及其应用河南省百所名校2022届普通高校招生全国统一考试猜题压轴卷理科数学试题(已下线)2022年全国高考甲卷数学(理)试题变式题9-12题(已下线)2022年全国高考甲卷数学(理)试题变式题9-12题(已下线)2022年高考浙江数学高考真题变式题10-12题(已下线)专题24 立体几何解答题最全归纳总结-1(已下线)2022年全国高考甲卷数学(理)试题变式题17-20题(已下线)2022年高考浙江数学高考真题变式题19-22题陕西省铜川市耀州中学2022届高三下学期热身冲刺考理科数学试题四川省泸县第四中学2022-2023学年高三上学期第三学月考试数学(理科)试题(已下线)模块一 专题1 《立体几何》单元检测篇 A基础卷
名校
解题方法
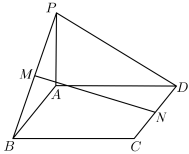
7 . 如图,已知四边形 是矩形,
是矩形, 平面
平面 ,且
,且 ,M、N是线段
,M、N是线段 、
、 上的点,满足
上的点,满足 .
. ,求证:直线
,求证:直线
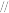 平面
平面 ;
;
(2)是否存在实数 ,使直线
,使直线 同时垂直于直线
同时垂直于直线 ,直线
,直线 ?如果有请求出
?如果有请求出 的值,否则请说明理由;
的值,否则请说明理由;
(3)若 ,求直线
,求直线 与直线
与直线 所成角的最大值.
所成角的最大值.
 是矩形,
是矩形, 平面
平面 ,且
,且 ,M、N是线段
,M、N是线段 、
、 上的点,满足
上的点,满足 .
.
 ,求证:直线
,求证:直线
 平面
平面 ;
;(2)是否存在实数
 ,使直线
,使直线 同时垂直于直线
同时垂直于直线 ,直线
,直线 ?如果有请求出
?如果有请求出 的值,否则请说明理由;
的值,否则请说明理由;(3)若
 ,求直线
,求直线 与直线
与直线 所成角的最大值.
所成角的最大值.
您最近一年使用:0次
2022-05-07更新
|
453次组卷
|
4卷引用:上海市控江中学2021-2022学年高二下学期期中数学试题
上海市控江中学2021-2022学年高二下学期期中数学试题第10章 空间直线与平面(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(沪教版2020必修第三册)(已下线)10.3 直线与平面所成的角 (第4课时)(作业)(夯实基础+能力提升)-【教材配套课件+作业】2022-2023学年高二数学精品教学课件(沪教版2020必修第三册)【温故练】第10章 空间直线与平面 单元测试-沪教版(2020)必修第三册
解题方法
8 . “加工六角螺母,只需六个侧面都是矩形,那么六条侧棱一定都垂直于上下两面”,这个论断用到了什么原理______ .
您最近一年使用:0次
2022-04-24更新
|
20次组卷
|
2卷引用:【课堂练】 10.3.2 直线与平面垂直 随堂练习-沪教版(2020)必修第三册 第10章 空间直线与平面
9 . 我们知道,在平面几何中,已知 三边边长分别为
三边边长分别为 ,面积为
,面积为 ,在
,在 内一点到三条边的距离相等设为
内一点到三条边的距离相等设为 ,则有
,则有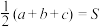 .现有三棱锥
.现有三棱锥 的两条棱
的两条棱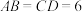 ,其余各棱长均为5,三棱锥
,其余各棱长均为5,三棱锥 内有一点
内有一点 到四个面的距离相等,则此距离等于
到四个面的距离相等,则此距离等于___________
 三边边长分别为
三边边长分别为 ,面积为
,面积为 ,在
,在 内一点到三条边的距离相等设为
内一点到三条边的距离相等设为 ,则有
,则有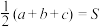 .现有三棱锥
.现有三棱锥 的两条棱
的两条棱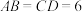 ,其余各棱长均为5,三棱锥
,其余各棱长均为5,三棱锥 内有一点
内有一点 到四个面的距离相等,则此距离等于
到四个面的距离相等,则此距离等于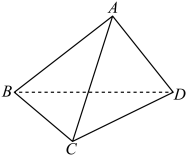
您最近一年使用:0次
名校
10 . 棱柱成为直棱柱的一个必要但不充分条件是( )
| A.有一条侧棱与底面的两边垂直 | B.有一条侧棱与底面垂直 |
| C.有一个侧面与底面的一条边垂直 | D.有两个相邻的侧面是矩形 |
您最近一年使用:0次



