1 . 在椭圆(双曲线)中,任意两条互相垂直的切线的交点都在同一个圆上,该圆的圆心是椭圆(双曲线)的中心,半径等于椭圆(双曲线)长半轴(实半轴)与短半轴(虚半轴)平方和(差)的算术平方根,则这个圆叫蒙日圆.已知椭圆 的蒙日圆的面积为
的蒙日圆的面积为 ,该椭圆的上顶点和下顶点分别为
,该椭圆的上顶点和下顶点分别为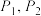 ,且
,且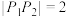 ,设过点
,设过点 的直线
的直线 与椭圆
与椭圆 交于
交于 两点(不与
两点(不与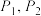 两点重合)且直线
两点重合)且直线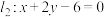 .
.
(1)证明: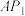 ,
,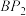 的交点
的交点 在直线
在直线 上;
上;
(2)求直线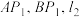 围成的三角形面积的最小值.
围成的三角形面积的最小值.
 的蒙日圆的面积为
的蒙日圆的面积为 ,该椭圆的上顶点和下顶点分别为
,该椭圆的上顶点和下顶点分别为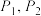 ,且
,且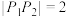 ,设过点
,设过点 的直线
的直线 与椭圆
与椭圆 交于
交于 两点(不与
两点(不与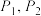 两点重合)且直线
两点重合)且直线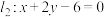 .
.(1)证明:
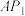 ,
,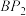 的交点
的交点 在直线
在直线 上;
上;(2)求直线
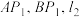 围成的三角形面积的最小值.
围成的三角形面积的最小值.
您最近半年使用:0次
2024-03-29更新
|
1808次组卷
|
4卷引用:湘豫名校联考2024年2月高三第一次模拟考试数学试题
湘豫名校联考2024年2月高三第一次模拟考试数学试题(已下线)重难点14 圆锥曲线必考压轴解答题全归类【十一大题型】(举一反三)(新高考专用)-2湖南省长沙市长郡中学2023-2024学年高三下学期适应考试(二)数学试题(已下线)江苏省泰州市2024届高三第二次调研测试数学试题变式题16-19
名校
解题方法
2 . 已知双曲线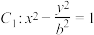 经过椭圆
经过椭圆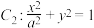 的左、右焦点
的左、右焦点 ,设
,设 的离心率分别为
的离心率分别为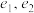 ,且
,且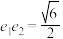 .
.
(1)求 的方程;
的方程;
(2)设 为
为 上一点,且在第一象限内,若直线
上一点,且在第一象限内,若直线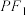 与
与 交于
交于 两点,直线
两点,直线 与
与 交于
交于 两点,设
两点,设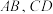 的中点分别为
的中点分别为 ,记直线
,记直线 的斜率为
的斜率为 ,当
,当 取最小值时,求点
取最小值时,求点 的坐标.
的坐标.
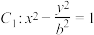 经过椭圆
经过椭圆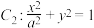 的左、右焦点
的左、右焦点 ,设
,设 的离心率分别为
的离心率分别为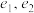 ,且
,且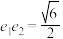 .
.(1)求
 的方程;
的方程;(2)设
 为
为 上一点,且在第一象限内,若直线
上一点,且在第一象限内,若直线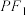 与
与 交于
交于 两点,直线
两点,直线 与
与 交于
交于 两点,设
两点,设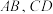 的中点分别为
的中点分别为 ,记直线
,记直线 的斜率为
的斜率为 ,当
,当 取最小值时,求点
取最小值时,求点 的坐标.
的坐标.
您最近半年使用:0次
2024-03-14更新
|
2040次组卷
|
4卷引用:湖北省八市2024届高三下学期3月联考数学试卷
名校
解题方法
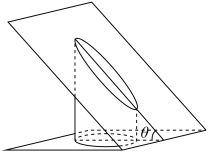
3 . 如图,用一个与圆柱底面成 角的平面截圆柱,截面是一个椭圆. 已知圆柱的底面半径为1,建立适当的平面直角坐标系
角的平面截圆柱,截面是一个椭圆. 已知圆柱的底面半径为1,建立适当的平面直角坐标系 ,可以得到椭圆
,可以得到椭圆 的标准方程:
的标准方程: .
.  的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 作斜率为
作斜率为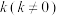 的直线
的直线 ,与
,与 交于
交于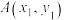 、
、 两点.
两点.
(1)求 的标准方程;
的标准方程;
(2)若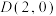 ,直线
,直线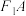 与
与 的交点
的交点 在直线
在直线 上,求
上,求 的值.
的值.
 角的平面截圆柱,截面是一个椭圆. 已知圆柱的底面半径为1,建立适当的平面直角坐标系
角的平面截圆柱,截面是一个椭圆. 已知圆柱的底面半径为1,建立适当的平面直角坐标系 ,可以得到椭圆
,可以得到椭圆 的标准方程:
的标准方程: .
.  的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 作斜率为
作斜率为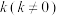 的直线
的直线 ,与
,与 交于
交于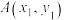 、
、 两点.
两点.
(1)求
 的标准方程;
的标准方程;(2)若
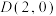 ,直线
,直线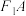 与
与 的交点
的交点 在直线
在直线 上,求
上,求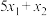 的值.
的值.
您最近半年使用:0次
解题方法
4 . 已知椭圆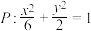 的焦点是椭圆
的焦点是椭圆 的顶点,椭圆
的顶点,椭圆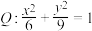 的焦点也是
的焦点也是 的顶点.
的顶点.
(1)求
 的方程;
的方程;(2)若
 ,
, ,
, 三点均在
三点均在 上,且
上,且 ,直线
,直线 ,
,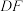 ,
, 的斜率均存在,证明:直线
的斜率均存在,证明:直线 过定点(用
过定点(用 ,
,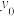 表示).
表示).
您最近半年使用:0次
23-24高二上·贵州铜仁·期末
5 . 已知椭圆 的焦点坐标
的焦点坐标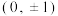 ,且过点
,且过点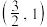 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)直线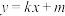 与椭圆
与椭圆 交于
交于 ,
, 两点,且
两点,且 ,
, 关于原点的对称点分别为
关于原点的对称点分别为 ,
, ,若
,若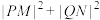 是一个与
是一个与 无关的常数,求此时的常数及四边形
无关的常数,求此时的常数及四边形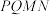 面积的最大值.
面积的最大值.
 的焦点坐标
的焦点坐标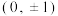 ,且过点
,且过点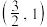 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)直线
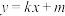 与椭圆
与椭圆 交于
交于 ,
, 两点,且
两点,且 ,
, 关于原点的对称点分别为
关于原点的对称点分别为 ,
, ,若
,若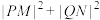 是一个与
是一个与 无关的常数,求此时的常数及四边形
无关的常数,求此时的常数及四边形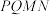 面积的最大值.
面积的最大值.
您最近半年使用:0次
23-24高二上·贵州贵阳·期末
解题方法
6 . 阅读材料:
在平面直角坐标系中,若点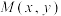 与定点
与定点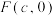 (或
(或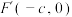 的距离和它到定直线
的距离和它到定直线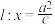 (或
(或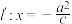 )的距离之比是常数
)的距离之比是常数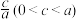 ,则
,则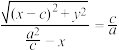 ,化简可得
,化简可得 ,设
,设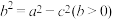 ,则得到方程
,则得到方程 ,所以点
,所以点 的轨迹是一个椭圆,这是从另一个角度给出了椭圆的定义.这里定点
的轨迹是一个椭圆,这是从另一个角度给出了椭圆的定义.这里定点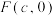 是椭圆的一个焦点,直线
是椭圆的一个焦点,直线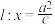 称为相应于焦点
称为相应于焦点 的准线;定点
的准线;定点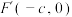 是椭圆的另一个焦点,直线
是椭圆的另一个焦点,直线 称为相应于焦点
称为相应于焦点 的准线.
的准线.
根据椭圆的这个定义,我们可以把到焦点的距离转化为到准线的距离.若点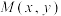 在椭圆
在椭圆 上,
上,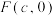 是椭圆的右焦点,椭圆的离心率
是椭圆的右焦点,椭圆的离心率 ,则点
,则点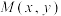 到准线
到准线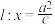 的距离为
的距离为 ,所以
,所以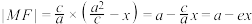 ,我们把这个公式称为椭圆的焦半径公式.
,我们把这个公式称为椭圆的焦半径公式.
结合阅读材料回答下面的问题:
已知椭圆 的右焦点为
的右焦点为 ,点
,点 是该椭圆上第一象限的点,且
是该椭圆上第一象限的点,且 轴,若直线
轴,若直线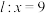 是椭圆右准线方程,点
是椭圆右准线方程,点 到直线
到直线 的距离为8.
的距离为8.
(1)求点 的坐标;
的坐标;
(2)若点 也在椭圆
也在椭圆 上且
上且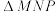 的重心为
的重心为 ,判断
,判断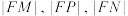 是否能构成等差数列?如果能,求出该等差数列的公差,如果不能,说明理由.
是否能构成等差数列?如果能,求出该等差数列的公差,如果不能,说明理由.
在平面直角坐标系中,若点
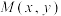 与定点
与定点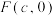 (或
(或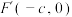 的距离和它到定直线
的距离和它到定直线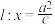 (或
(或 )的距离之比是常数
)的距离之比是常数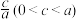 ,则
,则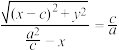 ,化简可得
,化简可得 ,设
,设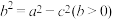 ,则得到方程
,则得到方程 ,所以点
,所以点 的轨迹是一个椭圆,这是从另一个角度给出了椭圆的定义.这里定点
的轨迹是一个椭圆,这是从另一个角度给出了椭圆的定义.这里定点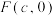 是椭圆的一个焦点,直线
是椭圆的一个焦点,直线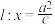 称为相应于焦点
称为相应于焦点 的准线;定点
的准线;定点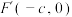 是椭圆的另一个焦点,直线
是椭圆的另一个焦点,直线 称为相应于焦点
称为相应于焦点 的准线.
的准线.根据椭圆的这个定义,我们可以把到焦点的距离转化为到准线的距离.若点
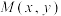 在椭圆
在椭圆 上,
上,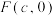 是椭圆的右焦点,椭圆的离心率
是椭圆的右焦点,椭圆的离心率 ,则点
,则点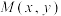 到准线
到准线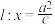 的距离为
的距离为 ,所以
,所以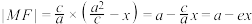 ,我们把这个公式称为椭圆的焦半径公式.
,我们把这个公式称为椭圆的焦半径公式.结合阅读材料回答下面的问题:
已知椭圆
 的右焦点为
的右焦点为 ,点
,点 是该椭圆上第一象限的点,且
是该椭圆上第一象限的点,且 轴,若直线
轴,若直线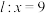 是椭圆右准线方程,点
是椭圆右准线方程,点 到直线
到直线 的距离为8.
的距离为8.(1)求点
 的坐标;
的坐标;(2)若点
 也在椭圆
也在椭圆 上且
上且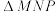 的重心为
的重心为 ,判断
,判断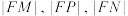 是否能构成等差数列?如果能,求出该等差数列的公差,如果不能,说明理由.
是否能构成等差数列?如果能,求出该等差数列的公差,如果不能,说明理由.
您最近半年使用:0次
解题方法
7 . 已知如图,点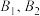 为椭圆
为椭圆 的短轴的两个端点,且
的短轴的两个端点,且 的坐标为
的坐标为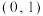 ,椭圆
,椭圆 的离心率为
的离心率为 .
.

(1)求椭圆 的标准方程;
的标准方程;
(2)若直线 不经过椭圆
不经过椭圆 的中心,且分别交椭圆
的中心,且分别交椭圆 与直线
与直线 于不同的三点
于不同的三点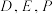 (点
(点 在线段
在线段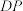 上),直线
上),直线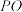 分别交直线
分别交直线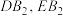 于点
于点 .求证:四边形
.求证:四边形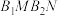 为平行四边形.
为平行四边形.
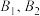 为椭圆
为椭圆 的短轴的两个端点,且
的短轴的两个端点,且 的坐标为
的坐标为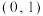 ,椭圆
,椭圆 的离心率为
的离心率为 .
.
(1)求椭圆
 的标准方程;
的标准方程;(2)若直线
 不经过椭圆
不经过椭圆 的中心,且分别交椭圆
的中心,且分别交椭圆 与直线
与直线 于不同的三点
于不同的三点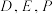 (点
(点 在线段
在线段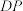 上),直线
上),直线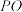 分别交直线
分别交直线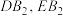 于点
于点 .求证:四边形
.求证:四边形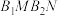 为平行四边形.
为平行四边形.
您最近半年使用:0次
2024-01-10更新
|
1491次组卷
|
3卷引用:辽宁省沈阳市2023-2024学年高三上学期教学质量监测(一)数学试题
名校
解题方法
8 . 已知记离心率为 的椭圆C的中心在顶点,焦点在x轴上,短轴长为
的椭圆C的中心在顶点,焦点在x轴上,短轴长为 .
.
(1)求椭圆C的标准方程;
(2)设椭圆C的左、右顶点分别为A1、A2,点Q在第一象限且QA2⊥A1A2,直线QA1与椭圆C的另一个交点为P.设椭圆C的右焦点为F2,线段QA2的中点M到直线PF2的距离为d,求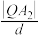 的值.
的值.
 的椭圆C的中心在顶点,焦点在x轴上,短轴长为
的椭圆C的中心在顶点,焦点在x轴上,短轴长为 .
.(1)求椭圆C的标准方程;
(2)设椭圆C的左、右顶点分别为A1、A2,点Q在第一象限且QA2⊥A1A2,直线QA1与椭圆C的另一个交点为P.设椭圆C的右焦点为F2,线段QA2的中点M到直线PF2的距离为d,求
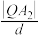 的值.
的值.
您最近半年使用:0次
23-24高二上·贵州贵阳·阶段练习
名校
解题方法
9 . 请阅读下列材料,并解决问题: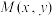 到一个定点
到一个定点 的距离和
的距离和 到定直线
到定直线 的距离的比是常数
的距离的比是常数 ,则动点的轨迹就是圆锥曲线(这个圆锥曲线的第二定义).其中定点
,则动点的轨迹就是圆锥曲线(这个圆锥曲线的第二定义).其中定点 称为其焦点,定直线
称为其焦点,定直线 称为其准线(其中椭圆与双曲线的准线方程为
称为其准线(其中椭圆与双曲线的准线方程为 ,抛物线准线方程为
,抛物线准线方程为 ),正常数
),正常数 称为其离心率.当
称为其离心率.当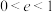 时,轨迹为椭圆;当
时,轨迹为椭圆;当 时,轨迹为抛物线;当
时,轨迹为抛物线;当 时,轨迹为双曲线.
时,轨迹为双曲线.
(1)已知平面内的动点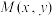 到一个定点
到一个定点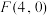 的距离和
的距离和 到定直线
到定直线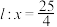 的距离的比是常数
的距离的比是常数 ,则动点
,则动点 的轨迹方程为 (直接写出结果,无需过程).
的轨迹方程为 (直接写出结果,无需过程).
(2)在(1)所求的曲线中是否存在一点,使得该点到直线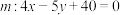 的距离最小?最小距离是多少?
的距离最小?最小距离是多少?
圆锥曲线的第二定义
二次曲线,即圆锥曲线,是由一平面截二次锥面得到的曲线,包括椭圆,抛物线,双曲线等.2000多年前,古希腊数学家最先开始研究二次曲线,并获得了大量的成果.古希腊数学家阿波罗尼斯采用平面切割圆锥的方法来研究二次曲线.阿波罗尼斯曾把椭圆叫“亏曲线”把双曲线叫做“超曲线”,把抛物线叫做“齐曲线”,事实上,二次曲线由很多统一的定义、统一的二级结论等等.比如:平面内的动点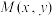 到一个定点
到一个定点 的距离和
的距离和 到定直线
到定直线 的距离的比是常数
的距离的比是常数 ,则动点的轨迹就是圆锥曲线(这个圆锥曲线的第二定义).其中定点
,则动点的轨迹就是圆锥曲线(这个圆锥曲线的第二定义).其中定点 称为其焦点,定直线
称为其焦点,定直线 称为其准线(其中椭圆与双曲线的准线方程为
称为其准线(其中椭圆与双曲线的准线方程为 ,抛物线准线方程为
,抛物线准线方程为 ),正常数
),正常数 称为其离心率.当
称为其离心率.当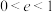 时,轨迹为椭圆;当
时,轨迹为椭圆;当 时,轨迹为抛物线;当
时,轨迹为抛物线;当 时,轨迹为双曲线.
时,轨迹为双曲线.(1)已知平面内的动点
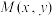 到一个定点
到一个定点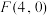 的距离和
的距离和 到定直线
到定直线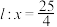 的距离的比是常数
的距离的比是常数 ,则动点
,则动点 的轨迹方程为 (直接写出结果,无需过程).
的轨迹方程为 (直接写出结果,无需过程).(2)在(1)所求的曲线中是否存在一点,使得该点到直线
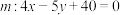 的距离最小?最小距离是多少?
的距离最小?最小距离是多少?
您最近半年使用:0次
2023-12-28更新
|
358次组卷
|
3卷引用:专题2 点点距离 构造函数 练
名校
解题方法
10 . 圆 称为椭圆
称为椭圆 的蒙日圆.已知椭圆
的蒙日圆.已知椭圆 :
: 的离心率为
的离心率为 ,
, 的蒙日圆方程为
的蒙日圆方程为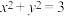 .
.
(1)求 的方程;
的方程;
(2)若 为
为 的左焦点,过
的左焦点,过 上的一点
上的一点 作
作 的切线
的切线 ,
, 与
与 的蒙日圆交于
的蒙日圆交于 ,
, 两点,过
两点,过 作直线
作直线 与
与 交于
交于 ,
, 两点,且
两点,且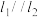 ,证明:
,证明: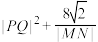 是定值.
是定值.
 称为椭圆
称为椭圆 的蒙日圆.已知椭圆
的蒙日圆.已知椭圆 :
: 的离心率为
的离心率为 ,
, 的蒙日圆方程为
的蒙日圆方程为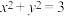 .
.(1)求
 的方程;
的方程;(2)若
 为
为 的左焦点,过
的左焦点,过 上的一点
上的一点 作
作 的切线
的切线 ,
, 与
与 的蒙日圆交于
的蒙日圆交于 ,
, 两点,过
两点,过 作直线
作直线 与
与 交于
交于 ,
, 两点,且
两点,且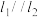 ,证明:
,证明: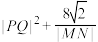 是定值.
是定值.
您最近半年使用:0次
2023-12-16更新
|
260次组卷
|
5卷引用:河北省保定市部分高中2024届高三上学期12月联考数学试题



