1 . 已知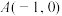 ,
,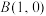 ,平面上有动点
,平面上有动点 ,且直线
,且直线 的斜率与直线
的斜率与直线 的斜率之积为1.
的斜率之积为1.
(1)求动点 的轨迹
的轨迹 的方程.
的方程.
(2)过点 的直线与
的直线与 交于点
交于点 (
( 在第一象限),过点
在第一象限),过点 的直线与
的直线与 交于点
交于点 (
( 在第三象限),记直线
在第三象限),记直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,且
,且 .
.
①求证:直线 过定点;
过定点;
②试判断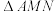 与
与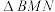 的面积之比是否为定值,若为定值,请求出该定值;若不为定值,请说明理由.
的面积之比是否为定值,若为定值,请求出该定值;若不为定值,请说明理由.
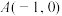 ,
,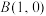 ,平面上有动点
,平面上有动点 ,且直线
,且直线 的斜率与直线
的斜率与直线 的斜率之积为1.
的斜率之积为1.(1)求动点
 的轨迹
的轨迹 的方程.
的方程.(2)过点
 的直线与
的直线与 交于点
交于点 (
( 在第一象限),过点
在第一象限),过点 的直线与
的直线与 交于点
交于点 (
( 在第三象限),记直线
在第三象限),记直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,且
,且 .
.①求证:直线
 过定点;
过定点;②试判断
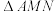 与
与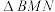 的面积之比是否为定值,若为定值,请求出该定值;若不为定值,请说明理由.
的面积之比是否为定值,若为定值,请求出该定值;若不为定值,请说明理由.
您最近一年使用:0次
2 . 设直线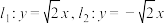 .点
.点 和点
和点 分别在直线
分别在直线 和
和 上运动,点
上运动,点 为
为 的中点,点
的中点,点 为坐标原点,且
为坐标原点,且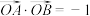 .
.
(1)已知直线 :
: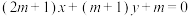 经过定点P,直线
经过定点P,直线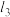 经过点P,且
经过点P,且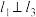 ,求直线
,求直线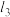 的方程.
的方程.
(2)求点 的轨迹方程
的轨迹方程 ;
;
(3)当直线 的斜率存在时,设点
的斜率存在时,设点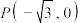 关于直线
关于直线 的对称点为
的对称点为 ,证明:直线
,证明:直线 过定点.
过定点.
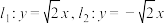 .点
.点 和点
和点 分别在直线
分别在直线 和
和 上运动,点
上运动,点 为
为 的中点,点
的中点,点 为坐标原点,且
为坐标原点,且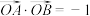 .
.(1)已知直线
 :
: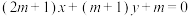 经过定点P,直线
经过定点P,直线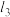 经过点P,且
经过点P,且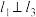 ,求直线
,求直线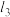 的方程.
的方程.(2)求点
 的轨迹方程
的轨迹方程 ;
;(3)当直线
 的斜率存在时,设点
的斜率存在时,设点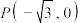 关于直线
关于直线 的对称点为
的对称点为 ,证明:直线
,证明:直线 过定点.
过定点.
您最近一年使用:0次
名校
解题方法
3 . 已知双曲线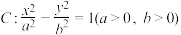 的两条渐近线方程为
的两条渐近线方程为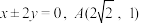 为
为 上一点.
上一点.
(1)求双曲线 的方程;
的方程;
(2)若过点 的直线
的直线 与
与 仅有1个公共点,求
仅有1个公共点,求 的方程;
的方程;
(3)过双曲线 的右焦点
的右焦点 作两条互相垂直的直线
作两条互相垂直的直线 ,
, ,且
,且 与
与 交于
交于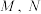 两点,记
两点,记 的中点
的中点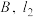 与
与 交于
交于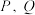 两点,记
两点,记 的中点为
的中点为 .若
.若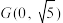 ,求点
,求点 到直线
到直线 的距离的最大值.
的距离的最大值.
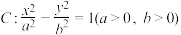 的两条渐近线方程为
的两条渐近线方程为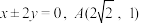 为
为 上一点.
上一点.(1)求双曲线
 的方程;
的方程;(2)若过点
 的直线
的直线 与
与 仅有1个公共点,求
仅有1个公共点,求 的方程;
的方程;(3)过双曲线
 的右焦点
的右焦点 作两条互相垂直的直线
作两条互相垂直的直线 ,
, ,且
,且 与
与 交于
交于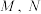 两点,记
两点,记 的中点
的中点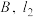 与
与 交于
交于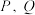 两点,记
两点,记 的中点为
的中点为 .若
.若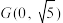 ,求点
,求点 到直线
到直线 的距离的最大值.
的距离的最大值.
您最近一年使用:0次
4 . 已知双曲线 的离心率为
的离心率为 ,
, ,
, 分别为其左、右焦点,P为双曲线上任一点,
分别为其左、右焦点,P为双曲线上任一点,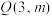 是双曲线在第一象限内的点,
是双曲线在第一象限内的点,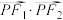 的最小值是
的最小值是 .
.
(1)过点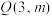 分别作双曲线C的两条渐近线的平行线,与渐近线分别交于A,B两点,O为坐标原点,求四边形OAQB的面积;
分别作双曲线C的两条渐近线的平行线,与渐近线分别交于A,B两点,O为坐标原点,求四边形OAQB的面积;
(2)若不过点Q的直线l与双曲线交于不同的两点M,N,且满足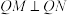 .证明:直线MN过定点,并求出该定点坐标.
.证明:直线MN过定点,并求出该定点坐标.
 的离心率为
的离心率为 ,
, ,
, 分别为其左、右焦点,P为双曲线上任一点,
分别为其左、右焦点,P为双曲线上任一点,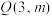 是双曲线在第一象限内的点,
是双曲线在第一象限内的点,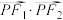 的最小值是
的最小值是 .
.(1)过点
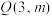 分别作双曲线C的两条渐近线的平行线,与渐近线分别交于A,B两点,O为坐标原点,求四边形OAQB的面积;
分别作双曲线C的两条渐近线的平行线,与渐近线分别交于A,B两点,O为坐标原点,求四边形OAQB的面积;(2)若不过点Q的直线l与双曲线交于不同的两点M,N,且满足
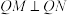 .证明:直线MN过定点,并求出该定点坐标.
.证明:直线MN过定点,并求出该定点坐标.
您最近一年使用:0次
名校
解题方法
5 . 已知动圆P过点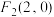 ,并且与圆
,并且与圆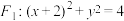 外切,设动圆的圆心P的轨迹为C.
外切,设动圆的圆心P的轨迹为C.
(1)直线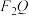 与圆
与圆 相切于点Q,求
相切于点Q,求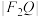 的值;
的值;
(2)求曲线C的方程;
(3)过点 的直线
的直线 与曲线C交于E,F两点,设直线
与曲线C交于E,F两点,设直线 ,点
,点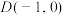 ,直线
,直线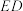 交
交 于点M,证明直线
于点M,证明直线 经过定点,并求出该定点的坐标.
经过定点,并求出该定点的坐标.
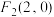 ,并且与圆
,并且与圆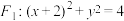 外切,设动圆的圆心P的轨迹为C.
外切,设动圆的圆心P的轨迹为C.(1)直线
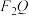 与圆
与圆 相切于点Q,求
相切于点Q,求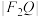 的值;
的值;(2)求曲线C的方程;
(3)过点
 的直线
的直线 与曲线C交于E,F两点,设直线
与曲线C交于E,F两点,设直线 ,点
,点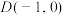 ,直线
,直线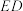 交
交 于点M,证明直线
于点M,证明直线 经过定点,并求出该定点的坐标.
经过定点,并求出该定点的坐标.
您最近一年使用:0次
2024-07-08更新
|
793次组卷
|
7卷引用:广东省东莞市虎门外语学校2024-2025学年高三上学期10月月考数学试题
广东省东莞市虎门外语学校2024-2025学年高三上学期10月月考数学试题江苏省徐州市铜山区大许中学2024-2025学年高二上学期第一次月考数学试卷.浙江省杭师大附2023-2024学年高二下学期期中数学试题(已下线)第48题 双曲线中的定点问题(高二暑假弯道超车)(已下线)直线与圆锥曲线的位置关系-一轮复习考点专练河南省驻马店市新蔡县第一高级中学2025届高三上学期8月开学考试数学试题(已下线)重组5 高二期中真题重组卷(湖北卷)B提升卷
6 . 已知双曲线 的离心率为
的离心率为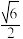 ,右顶点为
,右顶点为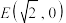 .
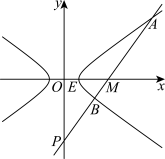
. 为双曲线
为双曲线 右支上两点,且点
右支上两点,且点 在第一象限,以
在第一象限,以 为直径的圆经过点
为直径的圆经过点 .
. 的方程;
的方程;
(2)证明:直线 恒过定点;
恒过定点;
(3)若直线 与
与 轴分别交于点
轴分别交于点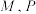 ,且
,且 为
为 中点,求
中点,求 的值.
的值.
 的离心率为
的离心率为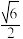 ,右顶点为
,右顶点为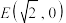 .
. 为双曲线
为双曲线 右支上两点,且点
右支上两点,且点 在第一象限,以
在第一象限,以 为直径的圆经过点
为直径的圆经过点 .
.
 的方程;
的方程;(2)证明:直线
 恒过定点;
恒过定点;(3)若直线
 与
与 轴分别交于点
轴分别交于点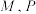 ,且
,且 为
为 中点,求
中点,求 的值.
的值.
您最近一年使用:0次
2024-06-28更新
|
552次组卷
|
3卷引用:江苏省南京市九中、十三中2024-2025年高三上学期8月阶段性学情检测数学试题
7 . 已知双曲线 的焦距为
的焦距为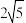 ,点
,点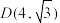 在C上.
在C上.
(1)求C的方程;
(2)直线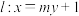 与C的右支交于
与C的右支交于 两点,点
两点,点 与点
与点 关于
关于 轴对称,
轴对称, 点在
点在 轴上的投影为
轴上的投影为 .
.
①求 的取值范围;
的取值范围;
②求证:直线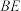 过点
过点 .
.
 的焦距为
的焦距为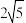 ,点
,点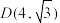 在C上.
在C上.(1)求C的方程;
(2)直线
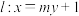 与C的右支交于
与C的右支交于 两点,点
两点,点 与点
与点 关于
关于 轴对称,
轴对称, 点在
点在 轴上的投影为
轴上的投影为 .
.①求
 的取值范围;
的取值范围;②求证:直线
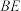 过点
过点 .
.
您最近一年使用:0次
2024-06-20更新
|
432次组卷
|
7卷引用:广东省普宁二中实验学校2023-2024学年高二下学期第三次月考数学试题
广东省普宁二中实验学校2023-2024学年高二下学期第三次月考数学试题黑龙江省双鸭山市友谊县高级中学2024届高三下学期高考模拟(一)数学试题(已下线)数学(广东专用03,新题型结构)广东省梅县东山中学2024届高三下学期第一次模拟考试数学试题四川省成都外国语学校2024届高三高考模拟(六)理科数学试题(已下线)专题10 解析几何中的定点问题(一)【讲】(压轴大全)(已下线)3.2.2 双曲线的简单几何性质——课堂例题
8 . 设A,B是双曲线H: 上的两点.直线l与双曲线H的交点为P,Q两点.
上的两点.直线l与双曲线H的交点为P,Q两点.
(1)若双曲线H的离心率是 ,且点
,且点 在双曲线H上,求双曲线H的方程;
在双曲线H上,求双曲线H的方程;
(2)设A、B分别是双曲线H: 的左、右顶点,直线l平行于y轴.求直线AP与BQ斜率的乘积,并求直线AP与BQ的交点M的轨迹方程;
的左、右顶点,直线l平行于y轴.求直线AP与BQ斜率的乘积,并求直线AP与BQ的交点M的轨迹方程;
(3)设双曲线H: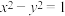 ,其中
,其中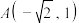 ,
, ,点M是抛物线C:
,点M是抛物线C: 上不同于点A、B的动点,且直线MA与双曲线H相交于另一点P,直线MB与双曲线H相交于另一点Q,问:直线PQ是否恒过某一定点?若是,求该定点的坐标;若不是,请说明理由.
上不同于点A、B的动点,且直线MA与双曲线H相交于另一点P,直线MB与双曲线H相交于另一点Q,问:直线PQ是否恒过某一定点?若是,求该定点的坐标;若不是,请说明理由.
 上的两点.直线l与双曲线H的交点为P,Q两点.
上的两点.直线l与双曲线H的交点为P,Q两点.(1)若双曲线H的离心率是
 ,且点
,且点 在双曲线H上,求双曲线H的方程;
在双曲线H上,求双曲线H的方程;(2)设A、B分别是双曲线H:
 的左、右顶点,直线l平行于y轴.求直线AP与BQ斜率的乘积,并求直线AP与BQ的交点M的轨迹方程;
的左、右顶点,直线l平行于y轴.求直线AP与BQ斜率的乘积,并求直线AP与BQ的交点M的轨迹方程;(3)设双曲线H:
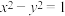 ,其中
,其中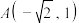 ,
, ,点M是抛物线C:
,点M是抛物线C: 上不同于点A、B的动点,且直线MA与双曲线H相交于另一点P,直线MB与双曲线H相交于另一点Q,问:直线PQ是否恒过某一定点?若是,求该定点的坐标;若不是,请说明理由.
上不同于点A、B的动点,且直线MA与双曲线H相交于另一点P,直线MB与双曲线H相交于另一点Q,问:直线PQ是否恒过某一定点?若是,求该定点的坐标;若不是,请说明理由.
您最近一年使用:0次
2024-06-10更新
|
890次组卷
|
6卷引用:上海市上海交通大学附属中学2025届高三上学期9月月考数学试卷
上海市上海交通大学附属中学2025届高三上学期9月月考数学试卷上海市复旦大学附属中学2023-2024学年高三下学期三模数学试题(已下线)专题2 解析几何中动点轨迹(方程)【练】(压轴题大全)海南省儋州市2022-2023学年高二上学期期末考试数学试题(已下线)专题6 圆锥曲线三定义及其应用【讲】(已下线)3.2.2 双曲线的简单几何性质——课后作业(提升版)
名校
解题方法
9 . 已知双曲线 的右焦点为
的右焦点为 ,双曲线
,双曲线 与抛物线
与抛物线
 交于点
交于点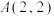 .
.
(1)求 的方程;
的方程;
(2)作直线 与
与 的两支分别交于点
的两支分别交于点 ,使得
,使得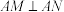 ,求证:直线
,求证:直线 过定点.
过定点.
 的右焦点为
的右焦点为 ,双曲线
,双曲线 与抛物线
与抛物线
 交于点
交于点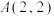 .
.(1)求
 的方程;
的方程;(2)作直线
 与
与 的两支分别交于点
的两支分别交于点 ,使得
,使得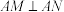 ,求证:直线
,求证:直线 过定点.
过定点.
您最近一年使用:0次
2024-05-29更新
|
482次组卷
|
2卷引用:云南省玉溪第一中学2023-2024学年高二下学期第二次月考数学试题
解题方法
10 . 已知双曲线 :
: (
( )与双曲线
)与双曲线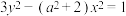 有相同的渐近线.
有相同的渐近线.
(1)求双曲线 的方程;
的方程;
(2)已知点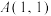 ,点
,点 ,
, 在双曲线
在双曲线 的左支上,满足
的左支上,满足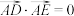 ,证明:直线
,证明:直线 过定点;
过定点;
(3)在(2)的条件下,求点 到直线
到直线 距离的最大值.
距离的最大值.
 :
: (
( )与双曲线
)与双曲线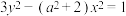 有相同的渐近线.
有相同的渐近线.(1)求双曲线
 的方程;
的方程;(2)已知点
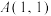 ,点
,点 ,
, 在双曲线
在双曲线 的左支上,满足
的左支上,满足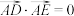 ,证明:直线
,证明:直线 过定点;
过定点;(3)在(2)的条件下,求点
 到直线
到直线 距离的最大值.
距离的最大值.
您最近一年使用:0次



