名校
1 . 已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用80元,设 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求 的分布列和均值(数学期望).
的分布列和均值(数学期望).
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用80元,设
 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求 的分布列和均值(数学期望).
的分布列和均值(数学期望).
您最近一年使用:0次
名校
解题方法
2 . 某单位在“全民健身日”举行了一场趣味运动会,其中一个项目为投篮游戏.游戏的规则如下:每局游戏需投篮3次,若投中的次数多于未投中的次数,该局得3分,否则得1分.已知甲投篮的命中率为 ,且每次投篮的结果相互独立.
,且每次投篮的结果相互独立.
(1)求甲在一局游戏中投篮命中次数X的分布列与期望;
(2)若参与者连续玩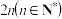 局投篮游戏获得的分数的平均值大于2,即可获得一份大奖.现有
局投篮游戏获得的分数的平均值大于2,即可获得一份大奖.现有 和
和 两种选择,要想获奖概率最大,甲应该如何选择?请说明理由.
两种选择,要想获奖概率最大,甲应该如何选择?请说明理由.
 ,且每次投篮的结果相互独立.
,且每次投篮的结果相互独立.(1)求甲在一局游戏中投篮命中次数X的分布列与期望;
(2)若参与者连续玩
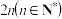 局投篮游戏获得的分数的平均值大于2,即可获得一份大奖.现有
局投篮游戏获得的分数的平均值大于2,即可获得一份大奖.现有 和
和 两种选择,要想获奖概率最大,甲应该如何选择?请说明理由.
两种选择,要想获奖概率最大,甲应该如何选择?请说明理由.
您最近一年使用:0次
2021-08-07更新
|
1931次组卷
|
6卷引用:江苏省连云港市2020-2021学年高二下学期期末数学试题
3 . 2020年以来,新冠病毒疫情肆虐全球我国在抗击新冠肺炎疫情中取得了世界瞩目的成绩,为其他国家提供了大量的医疗经验和防控措施.根据疫情防控需要现在要对某地区的
 份样本进行核酸检验,检测过程中每个样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验
份样本进行核酸检验,检测过程中每个样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验 次;②混合检验,将其中
次;②混合检验,将其中 (
(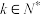 且
且 )份样本分别取样混合在一起检验,若检验结果为阴性,这
)份样本分别取样混合在一起检验,若检验结果为阴性,这 份的样本全为阴性,因而这
份的样本全为阴性,因而这 份样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份样本只要检验一次就够了,如果检验结果为阳性,为了明确这 份样本究竟哪几份为阳性,就要对这
份样本究竟哪几份为阳性,就要对这 份样本再逐份检验,此时这
份样本再逐份检验,此时这 份样本的检验次数总共为
份样本的检验次数总共为 次.假设在接受检验的样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
 .
.
(1)假设有10份样本,其中只有2份样本为阳性,现采用逐份检验方式对每一份样本进行检测,求经过3次检验就能把阳性样本全部检验出来的概率;
(2)现取其中 (
(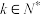 且
且 )份样本,每份样本是阳性结果的概率
)份样本,每份样本是阳性结果的概率 .记采用混合检验方式,样本需要检验的总次数为
.记采用混合检验方式,样本需要检验的总次数为 ,求
,求 的概率分布列及数学期望;并说明采用混合检验方式可以使得样本需要检验的总次数的期望比逐份检验的总次数期望少的
的概率分布列及数学期望;并说明采用混合检验方式可以使得样本需要检验的总次数的期望比逐份检验的总次数期望少的 的最大值是多少?
的最大值是多少?
(参考数据: ,
,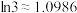 ,
,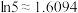 ,
,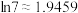 .)
.)

 份样本进行核酸检验,检测过程中每个样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验
份样本进行核酸检验,检测过程中每个样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验 次;②混合检验,将其中
次;②混合检验,将其中 (
(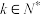 且
且 )份样本分别取样混合在一起检验,若检验结果为阴性,这
)份样本分别取样混合在一起检验,若检验结果为阴性,这 份的样本全为阴性,因而这
份的样本全为阴性,因而这 份样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份样本只要检验一次就够了,如果检验结果为阳性,为了明确这 份样本究竟哪几份为阳性,就要对这
份样本究竟哪几份为阳性,就要对这 份样本再逐份检验,此时这
份样本再逐份检验,此时这 份样本的检验次数总共为
份样本的检验次数总共为 次.假设在接受检验的样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
 .
.(1)假设有10份样本,其中只有2份样本为阳性,现采用逐份检验方式对每一份样本进行检测,求经过3次检验就能把阳性样本全部检验出来的概率;
(2)现取其中
 (
(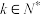 且
且 )份样本,每份样本是阳性结果的概率
)份样本,每份样本是阳性结果的概率 .记采用混合检验方式,样本需要检验的总次数为
.记采用混合检验方式,样本需要检验的总次数为 ,求
,求 的概率分布列及数学期望;并说明采用混合检验方式可以使得样本需要检验的总次数的期望比逐份检验的总次数期望少的
的概率分布列及数学期望;并说明采用混合检验方式可以使得样本需要检验的总次数的期望比逐份检验的总次数期望少的 的最大值是多少?
的最大值是多少?(参考数据:
 ,
,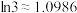 ,
,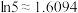 ,
,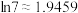 .)
.)
您最近一年使用:0次
2021-05-29更新
|
493次组卷
|
5卷引用:江苏省连云港市2021届高三下学期3.5模数学试题
江苏省连云港市2021届高三下学期3.5模数学试题江苏省连云港市2021届高三下学期高考考前一模数学试题(已下线)热点10 概率与统计-2022年高考数学【热点·重点·难点】专练(新高考专用)(已下线)押全国卷(理科)第18题 概率与统计-备战2022年高考数学(理)临考题号押题(全国卷)(已下线)专题26 概率综合问题(分布列)(解答题)(理科)-1
4 . 某奶茶店推出一款新品奶茶,每杯成本4元,售价6元.如果当天卖不完,剩下的奶茶只能倒掉.奶茶店记录了60天这款新品奶茶的日需求量,整理得下表:
以60天记录的各需求量的频率作为各需求量发生的概率.
(1)从这60天中任取2天,求这2天的日需求量至少有一天为35的概率;
(2)①若奶茶店一天准备了35杯这款新品奶茶,用 表示当天销售这款新品奶茶的利润(单位:元),求
表示当天销售这款新品奶茶的利润(单位:元),求 的分布列和数学期望;
的分布列和数学期望;
②假设奶茶店每天准备的这款新品奶茶倍数都是5的倍数,有顾客建议店主每天准备40杯这款新品奶茶,你认为店主应该接受这个建议吗?请说明理由.
| 日需求量杯数 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 天数 | 5 | 5 | 10 | 15 | 10 | 10 | 5 |
(1)从这60天中任取2天,求这2天的日需求量至少有一天为35的概率;
(2)①若奶茶店一天准备了35杯这款新品奶茶,用
 表示当天销售这款新品奶茶的利润(单位:元),求
表示当天销售这款新品奶茶的利润(单位:元),求 的分布列和数学期望;
的分布列和数学期望;②假设奶茶店每天准备的这款新品奶茶倍数都是5的倍数,有顾客建议店主每天准备40杯这款新品奶茶,你认为店主应该接受这个建议吗?请说明理由.
您最近一年使用:0次
2021-05-08更新
|
968次组卷
|
2卷引用:江苏省连云港市市四星级部分高中2020-2021学年高二下学期5月联考数学试题
解题方法
5 . 为加强进口冷链食品监管,某省于2020年底在全省建立进口冷链食品集中监管专仓制度,在口岸、目的地市或县(区、市)等进口冷链食品第一入境点,设立进口冷链食品集中监管专仓,集中开展核酸检测和预防性全面消毒工作,为了进一步确定某批进口冷冻食品是否感染病毒,在入关检疫时需要对其采样进行化验,若结果呈阳性,则有该病毒;若结果呈阴性,则没有该病毒,对于 ,(
,(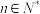 )份样本,有以下两种检验方式:一是逐份检验,则需检验
)份样本,有以下两种检验方式:一是逐份检验,则需检验 次:二是混合检验,将
次:二是混合检验,将 份样本分别取样混合在一起,若检验结果为阴性,那么这
份样本分别取样混合在一起,若检验结果为阴性,那么这 份全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这
份全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这 份究竟哪些为阳性,就需要对它们再次取样逐份检验,则
份究竟哪些为阳性,就需要对它们再次取样逐份检验,则 份检验的次数共为
份检验的次数共为 次,若每份样本没有该病毒的概率为
次,若每份样本没有该病毒的概率为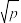 (
( ),而且样本之间是否有该病毒是相互独立的.
),而且样本之间是否有该病毒是相互独立的.
(1)若 ,求2份样本混合的结果为阳性的概率;
,求2份样本混合的结果为阳性的概率;
(2)若取得4份样本,考虑以下两种检验方案:方案一:采用混合检验;方案二:平均分成两组,每组2份样本采用混合检验.若检验次数的期望值越小,则方案越“优”,试问方案一、二哪个更“优”?请说明理由.
 ,(
,(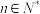 )份样本,有以下两种检验方式:一是逐份检验,则需检验
)份样本,有以下两种检验方式:一是逐份检验,则需检验 次:二是混合检验,将
次:二是混合检验,将 份样本分别取样混合在一起,若检验结果为阴性,那么这
份样本分别取样混合在一起,若检验结果为阴性,那么这 份全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这
份全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这 份究竟哪些为阳性,就需要对它们再次取样逐份检验,则
份究竟哪些为阳性,就需要对它们再次取样逐份检验,则 份检验的次数共为
份检验的次数共为 次,若每份样本没有该病毒的概率为
次,若每份样本没有该病毒的概率为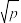 (
( ),而且样本之间是否有该病毒是相互独立的.
),而且样本之间是否有该病毒是相互独立的.(1)若
 ,求2份样本混合的结果为阳性的概率;
,求2份样本混合的结果为阳性的概率;(2)若取得4份样本,考虑以下两种检验方案:方案一:采用混合检验;方案二:平均分成两组,每组2份样本采用混合检验.若检验次数的期望值越小,则方案越“优”,试问方案一、二哪个更“优”?请说明理由.
您最近一年使用:0次
2021-03-21更新
|
1683次组卷
|
6卷引用:江苏省连云港市赣榆区2020-2021学年高二下学期期中数学试题
江苏省连云港市赣榆区2020-2021学年高二下学期期中数学试题山东省日照市2021届高三下学期一模数学试题(已下线)第四章 复习与小结 B提高练(已下线)必刷卷02-2021年高考数学考前信息必刷卷(江苏专用)(已下线)第四章 概率与统计 本章小结河南省郑州市京师杜甫高级中学2022-2023高三上学期第四次考试数学试题
名校
解题方法
6 . 今年年初,我市某医院计划从3名医生、5名护士中随机选派4人参加湖北新冠肺炎疫情狙击战.
(1)求选派的4人中至少有2名医生的概率;
(2)设选派的4人中医生人数为X,求X的概率分布和数学期望.
(1)求选派的4人中至少有2名医生的概率;
(2)设选派的4人中医生人数为X,求X的概率分布和数学期望.
您最近一年使用:0次
2020-07-17更新
|
247次组卷
|
4卷引用:江苏省连云港市2019-2020学年高二下学期期末数学试题
名校
解题方法
7 . 厂家在产品出厂前,需对产品做检验,第一次检测厂家的每件产品合格的概率为 ,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为
,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为 ,如果合格,则可以出厂,不合格则当废品回收.
,如果合格,则可以出厂,不合格则当废品回收.
 求某件产品能出厂的概率;
求某件产品能出厂的概率;
 若该产品的生产成本为
若该产品的生产成本为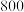 元/件,出厂价格为
元/件,出厂价格为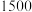 元/件,每次检测费为
元/件,每次检测费为 元/件,技术处理每次
元/件,技术处理每次 元/件,回收获利
元/件,回收获利 元/件.假如每件产品是否合格相互独立,记
元/件.假如每件产品是否合格相互独立,记 为任意一件产品所获得的利润,求随机变量
为任意一件产品所获得的利润,求随机变量 的分布列与数学期望.
的分布列与数学期望.
 ,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为
,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为 ,如果合格,则可以出厂,不合格则当废品回收.
,如果合格,则可以出厂,不合格则当废品回收. 求某件产品能出厂的概率;
求某件产品能出厂的概率; 若该产品的生产成本为
若该产品的生产成本为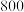 元/件,出厂价格为
元/件,出厂价格为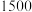 元/件,每次检测费为
元/件,每次检测费为 元/件,技术处理每次
元/件,技术处理每次 元/件,回收获利
元/件,回收获利 元/件.假如每件产品是否合格相互独立,记
元/件.假如每件产品是否合格相互独立,记 为任意一件产品所获得的利润,求随机变量
为任意一件产品所获得的利润,求随机变量 的分布列与数学期望.
的分布列与数学期望.
您最近一年使用:0次
2020-05-23更新
|
491次组卷
|
3卷引用:江苏省连云港市板浦高级中学2020-2021学年高三上学期期末模拟测试二数学试题
8 . 棋盘上标有第0,1,2,…,100站,棋子开始时位于第0站,棋手抛掷均匀硬币走跳棋游戏.若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到跳到第99站或第100站时,游戏结束.设棋子跳到第n站的概率为Pn.
(1)当游戏开始时若抛掷均匀硬币3次后求棋手所走站数之和X的分布列与数学期望;
(2)证明: ;
;
(3)求P99,P100的值.
(1)当游戏开始时若抛掷均匀硬币3次后求棋手所走站数之和X的分布列与数学期望;
(2)证明:
 ;
;(3)求P99,P100的值.
您最近一年使用:0次
2020-08-28更新
|
1189次组卷
|
9卷引用:2020届江苏省连云港市六所四星高中(海州高中、赣榆高中、海头中学、东海高中、新海高中、灌云高中)高三下学期模拟考试数学试题
2020届江苏省连云港市六所四星高中(海州高中、赣榆高中、海头中学、东海高中、新海高中、灌云高中)高三下学期模拟考试数学试题2019年安徽省江淮十校高三上学期第一次联考数学(理)试题2020届湖北省部分重点中学高三上学期期末联考理科数学试题2020届河北省衡水市武邑中学高三上学期期末数学(理)试题(已下线)专题09 数列与离散型随机变量相结合问题(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖江苏省盐城市滨海县八滩中学2020届高三下学期四模数学试题(已下线)【理科附加】专题05 随机变量及其分布-2020年高考数学母题题源解密(江苏专版)河北省石家庄正中实验中学2020-2021学年高二上学期第二次月考数学试题(已下线)专题11-2 概率与分布列大题归类-1
解题方法
9 . 羽毛球比赛中采用每球得分制,即每回合中胜方得1分,负方得0分,每回合由上回合的胜方发球.设在甲、乙的比赛中,每回合发球,发球方得1分的概率为0.6,各回合发球的胜负结果相互独立.若在一局比赛中,甲先发球.
(1)求比赛进行3个回合后,甲与乙的比分为 的概率;
的概率;
(2) 表示3个回合后乙的得分,求
表示3个回合后乙的得分,求 的分布列与数学期望.
的分布列与数学期望.
(1)求比赛进行3个回合后,甲与乙的比分为
 的概率;
的概率;(2)
 表示3个回合后乙的得分,求
表示3个回合后乙的得分,求 的分布列与数学期望.
的分布列与数学期望.
您最近一年使用:0次
2019-09-08更新
|
478次组卷
|
3卷引用:江苏省连云港市2018—2019学年度第二学期期末考试高二数学试题(理科)
10 . 某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间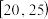 ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列.
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
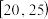 ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高 气温 | [10, 15) | [15, 20) | [20, 25) | [25, 30) | [30, 35) | [35, 40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列.
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
您最近一年使用:0次
2017-08-07更新
|
6690次组卷
|
33卷引用:江苏省南京师范大学灌云附属中学、灌南县第二中学2023-2024学年高三上学期10月阶段性联考数学试题
江苏省南京师范大学灌云附属中学、灌南县第二中学2023-2024学年高三上学期10月阶段性联考数学试题2017年全国普通高等学校招生统一考试理科数学(新课标3卷精编版)【全国市级联考】河南省南阳市2017-2018学年高二下学期期末考试数学(理)试题【全国市级联考】长春市普通高中2019届高三质量监测(一)理科数学试题【全国百强校】云南省昆明市黄冈实验学校2019届高三上学期期末考试数学(理)试题湖北省黄冈市2018-2019学年高二下学期期末数学(理)试题湖南省郴州市2019-2020学年高三第一次教学质量监测(12月) 数学(理)试题江苏省无锡市大桥实验学校2019-2020学年高二下学期期中数学试题河南省南阳市第一中学校2019-2020学年高二下学期第二次月考(5月)数学(理)试题(已下线)易错点11 概率统计-备战2021年新高考数学一轮复习易错题(已下线)突破2.1离散型随机变量及分其布列突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)河南省项城三高2019-2020学年度下学期第二次调研考试高二理科数学试题(已下线)专题32 概率和统计【理】-十年(2011-2020)高考真题数学分项(五)人教B版(2019) 选择性必修第二册 过关斩将 第四章 概率与统计 4.2 随机变量 4.2 综合拔高练(已下线)易错点13 概率与统计-备战2021年高考数学(理)一轮复习易错题(已下线)易错点13 概率与统计-备战2021年高考数学(文)一轮复习易错题(已下线)7.3 离散型随机变量的数字特征(精练)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)解密09 概率、随机变量及其分布列(讲义)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练四川省资阳市乐至中学2022届高三第一次质量检测数学(理科)试题北师大版(2019) 选修第一册 必杀技 第六章 素养检测人教A版(2019) 选修第三册 必杀技 第七章检测河北省武安市第一中学2022届高三上学期第五次调研数学试题(已下线)专题20统计概率解答题20题-备战2022年高考数学冲刺横向强化精练精讲(新高考专用)(已下线)专题52 盘点随机变量分布列及期望的问题——备战2022年高考数学二轮复习常考点专题突破(已下线)数学-2022年高考押题预测卷02(江苏专用)(已下线)专题13 概率统计解答题安徽省芜湖市第一中学2020届高三下学期3月第五次线上考试数学试题(已下线)模块三 专题6 概率与统计3.2 离散型随机变量及其分布列(已下线)第六节 离散型随机变量的数字特征(讲) 一轮复习点点通(已下线)8.4 离散型随机变量的分布列,期望与方差(高考真题素材之十年高考)(已下线)专题25 概率统计解答题(理科)-2专题33概率统计解答题(第二部分)



