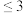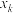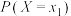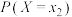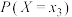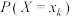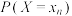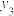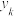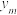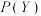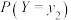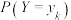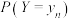1 . 随着科技的不断发展,人工智能技术在人类生产生活中的应用越来越广泛.为了解用户对 ,
, 两款人机交互软件(以下简称软件)的满意度,某平台随机选取了仅使用
两款人机交互软件(以下简称软件)的满意度,某平台随机选取了仅使用 款软件的用户和仅使用
款软件的用户和仅使用 款软件的用户各
款软件的用户各 人,采用打分方式进行调查,情况如下图:
人,采用打分方式进行调查,情况如下图:
假设用频率估计概率,且所有用户的打分情况相互独立.
(1)分别估计仅使用 款软件的全体用户和仅使用
款软件的全体用户和仅使用 款软件的全体用户对所使用软件的满意度为“非常满意”的概率;
款软件的全体用户对所使用软件的满意度为“非常满意”的概率;
(2)从仅使用 款软件的全体用户中随机选取
款软件的全体用户中随机选取 人,从仅使用
人,从仅使用 款软件的全体用户中随机选取
款软件的全体用户中随机选取 人,估计这
人,估计这 人中恰有
人中恰有 人对所使用软件的满意度为“非常满意”的概率;
人对所使用软件的满意度为“非常满意”的概率;
(3)从仅使用 ,
, 两款软件的全体用户中各随机选取
两款软件的全体用户中各随机选取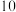 人进行电话回访,记
人进行电话回访,记 为仅使用
为仅使用 款软件的
款软件的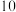 人中对所使用软件的满意度为“不满意”的人数,
人中对所使用软件的满意度为“不满意”的人数, 为仅使用
为仅使用 款软件的
款软件的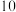 人中对所使用软件的满意度为“不满意”的人数,试比较
人中对所使用软件的满意度为“不满意”的人数,试比较 ,
, 的方差
的方差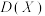 ,
,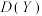 的大小.(结论不要求证明)
的大小.(结论不要求证明)
 ,
, 两款人机交互软件(以下简称软件)的满意度,某平台随机选取了仅使用
两款人机交互软件(以下简称软件)的满意度,某平台随机选取了仅使用 款软件的用户和仅使用
款软件的用户和仅使用 款软件的用户各
款软件的用户各 人,采用打分方式进行调查,情况如下图:
人,采用打分方式进行调查,情况如下图: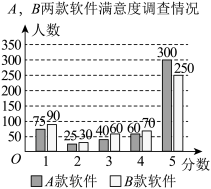
分数 |
|
|
|
满意度 | 非常满意 | 满意 | 不满意 |
(1)分别估计仅使用
 款软件的全体用户和仅使用
款软件的全体用户和仅使用 款软件的全体用户对所使用软件的满意度为“非常满意”的概率;
款软件的全体用户对所使用软件的满意度为“非常满意”的概率;(2)从仅使用
 款软件的全体用户中随机选取
款软件的全体用户中随机选取 人,从仅使用
人,从仅使用 款软件的全体用户中随机选取
款软件的全体用户中随机选取 人,估计这
人,估计这 人中恰有
人中恰有 人对所使用软件的满意度为“非常满意”的概率;
人对所使用软件的满意度为“非常满意”的概率;(3)从仅使用
 ,
, 两款软件的全体用户中各随机选取
两款软件的全体用户中各随机选取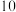 人进行电话回访,记
人进行电话回访,记 为仅使用
为仅使用 款软件的
款软件的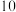 人中对所使用软件的满意度为“不满意”的人数,
人中对所使用软件的满意度为“不满意”的人数, 为仅使用
为仅使用 款软件的
款软件的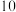 人中对所使用软件的满意度为“不满意”的人数,试比较
人中对所使用软件的满意度为“不满意”的人数,试比较 ,
, 的方差
的方差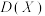 ,
,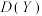 的大小.(结论不要求证明)
的大小.(结论不要求证明)
您最近一年使用:0次
2 . 组合投资需要同时考虑风险与收益.为了控制风险需要组合低风险资产,为了扩大收益需要组合高收益资产,现有两个相互独立的投资项目A和B,单独投资100万元项目A的收益记为随机变量X,单独投资100万元项目B的收益记为随机变量Y.若将100万资金按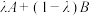 进行组合投资,则投资收益的随机变量Z满足
进行组合投资,则投资收益的随机变量Z满足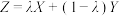 ,其中
,其中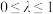 .假设在组合投资中,可用随机变量的期望衡量收益,可用随机变量的方差衡量风险.
.假设在组合投资中,可用随机变量的期望衡量收益,可用随机变量的方差衡量风险.
(1)若 ,
, ,求Z的期望与方差;
,求Z的期望与方差;
(2)已知随机变量X满足分布列:
随机变量Y满足分布列:
且随机变量X与Y相互独立,即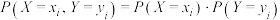 ,
,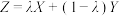 ,
,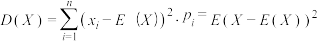 .求证:
.求证: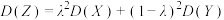 ;
;
(3)若投资项目X是高收益资产,其每年的收益满足:有30%的可能亏损当前资产的一半;有70%的可能增值当前资产的一倍.投资项目 是低风险资产,满足
是低风险资产,满足 .试问
.试问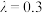 能否满足投资第1年的收益不低于17万,风险不高于500?请说明理由.
能否满足投资第1年的收益不低于17万,风险不高于500?请说明理由.
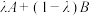 进行组合投资,则投资收益的随机变量Z满足
进行组合投资,则投资收益的随机变量Z满足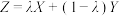 ,其中
,其中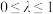 .假设在组合投资中,可用随机变量的期望衡量收益,可用随机变量的方差衡量风险.
.假设在组合投资中,可用随机变量的期望衡量收益,可用随机变量的方差衡量风险.(1)若
 ,
, ,求Z的期望与方差;
,求Z的期望与方差;(2)已知随机变量X满足分布列:
X |
|
|
| … |
| … |
|
|
|
|
| … |
| … |
|
Y |
|
|
| … |
| … |
|
|
|
|
| … |
| … |
|
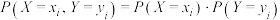 ,
,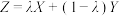 ,
,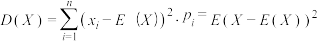 .求证:
.求证: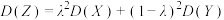 ;
;(3)若投资项目X是高收益资产,其每年的收益满足:有30%的可能亏损当前资产的一半;有70%的可能增值当前资产的一倍.投资项目
 是低风险资产,满足
是低风险资产,满足 .试问
.试问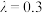 能否满足投资第1年的收益不低于17万,风险不高于500?请说明理由.
能否满足投资第1年的收益不低于17万,风险不高于500?请说明理由.
您最近一年使用:0次
解题方法
3 . 某区域中的物种 拥有两个亚种(分别记为
拥有两个亚种(分别记为 种和
种和 种).为了调查该区域中这两个亚种的数目,某生物研究小组计划在该区域中捕捉
种).为了调查该区域中这两个亚种的数目,某生物研究小组计划在该区域中捕捉 个物种
个物种 ,统计其中
,统计其中 种的数目后,将捕获的生物全部放回,作为一次试验结果.重复进行这个试验共
种的数目后,将捕获的生物全部放回,作为一次试验结果.重复进行这个试验共 次,记第
次,记第 次试验中
次试验中 种的数目为随机变量
种的数目为随机变量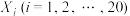 .设该区域中
.设该区域中 种的数目为
种的数目为 ,
, 种的数目为
种的数目为 ,每一次试验均相互独立.
,每一次试验均相互独立.
(1)求 的分布列;
的分布列;
(2)记随机变量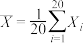 .已知
.已知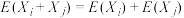 ,
,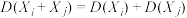 ;
;
(ⅰ)证明: ,
,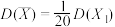 ;
;
(ⅱ)该小组完成所有试验后,得到 的实际取值分别为
的实际取值分别为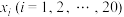 .数据
.数据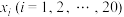 的平均值
的平均值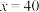 ,方差
,方差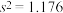 .采用
.采用 和
和 分别代替
分别代替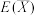 和
和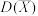 ,给出
,给出 ,
, 的估计值.
的估计值.
 拥有两个亚种(分别记为
拥有两个亚种(分别记为 种和
种和 种).为了调查该区域中这两个亚种的数目,某生物研究小组计划在该区域中捕捉
种).为了调查该区域中这两个亚种的数目,某生物研究小组计划在该区域中捕捉 个物种
个物种 ,统计其中
,统计其中 种的数目后,将捕获的生物全部放回,作为一次试验结果.重复进行这个试验共
种的数目后,将捕获的生物全部放回,作为一次试验结果.重复进行这个试验共 次,记第
次,记第 次试验中
次试验中 种的数目为随机变量
种的数目为随机变量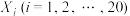 .设该区域中
.设该区域中 种的数目为
种的数目为 ,
, 种的数目为
种的数目为 ,每一次试验均相互独立.
,每一次试验均相互独立.(1)求
 的分布列;
的分布列;(2)记随机变量
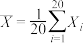 .已知
.已知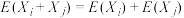 ,
,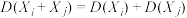 ;
;(ⅰ)证明:
 ,
,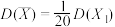 ;
;(ⅱ)该小组完成所有试验后,得到
 的实际取值分别为
的实际取值分别为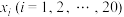 .数据
.数据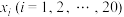 的平均值
的平均值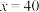 ,方差
,方差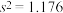 .采用
.采用 和
和 分别代替
分别代替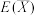 和
和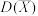 ,给出
,给出 ,
, 的估计值.
的估计值.
您最近一年使用:0次
2023-05-02更新
|
2834次组卷
|
9卷引用:湖北省星云联盟2023届高三下学期统一模拟考试Ⅱ数学试题
湖北省星云联盟2023届高三下学期统一模拟考试Ⅱ数学试题2023年普通高等学校招生星云线上统一模拟考试Ⅱ数学试题湖北省部分名校2023届高考适应性考试数学试题(已下线)第四篇 概率与统计 专题7 常见分布 微点1 常见分布(已下线)考点13 二项分布与超级几何分布 2024届高考数学考点总动员(已下线)随机变量及其分布(已下线)专题7.6 离散型随机变量及其分布大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第五章 概率统计创新问题 专题三 概率统计中的函数思想 微点1 概率统计中的函数思想(一)【培优版】
名校
解题方法
4 . 概率论中有很多经典的不等式,其中最著名的两个当属由两位俄国数学家马尔科夫和切比雪夫分别提出的马尔科夫(Markov)不等式和切比雪夫(Chebyshev)不等式.马尔科夫不等式的形式如下:
设 为一个非负随机变量,其数学期望为
为一个非负随机变量,其数学期望为 ,则对任意
,则对任意 ,均有
,均有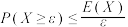 ,
,
马尔科夫不等式给出了随机变量取值不小于某正数的概率上界,阐释了随机变量尾部取值概率与其数学期望间的关系.当 为非负离散型随机变量时,马尔科夫不等式的证明如下:
为非负离散型随机变量时,马尔科夫不等式的证明如下:
设 的分布列为
的分布列为 其中
其中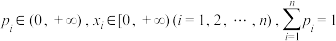 ,则对任意
,则对任意 ,
,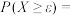
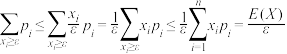 ,其中符号
,其中符号 表示对所有满足
表示对所有满足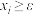 的指标
的指标 所对应的
所对应的 求和.
求和.
切比雪夫不等式的形式如下:
设随机变量 的期望为
的期望为 ,方差为
,方差为 ,则对任意
,则对任意 ,均有
,均有
(1)根据以上参考资料,证明切比雪夫不等式对离散型随机变量 成立.
成立.
(2)某药企研制出一种新药,宣称对治疗某种疾病的有效率为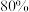 .现随机选择了100名患者,经过使用该药治疗后,治愈的人数为60人,请结合切比雪夫不等式通过计算说明药厂的宣传内容是否真实可信.
.现随机选择了100名患者,经过使用该药治疗后,治愈的人数为60人,请结合切比雪夫不等式通过计算说明药厂的宣传内容是否真实可信.
设
 为一个非负随机变量,其数学期望为
为一个非负随机变量,其数学期望为 ,则对任意
,则对任意 ,均有
,均有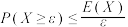 ,
,马尔科夫不等式给出了随机变量取值不小于某正数的概率上界,阐释了随机变量尾部取值概率与其数学期望间的关系.当
 为非负离散型随机变量时,马尔科夫不等式的证明如下:
为非负离散型随机变量时,马尔科夫不等式的证明如下:设
 的分布列为
的分布列为 其中
其中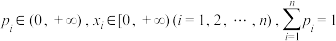 ,则对任意
,则对任意 ,
,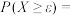
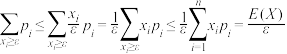 ,其中符号
,其中符号 表示对所有满足
表示对所有满足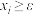 的指标
的指标 所对应的
所对应的 求和.
求和.切比雪夫不等式的形式如下:
设随机变量
 的期望为
的期望为 ,方差为
,方差为 ,则对任意
,则对任意 ,均有
,均有
(1)根据以上参考资料,证明切比雪夫不等式对离散型随机变量
 成立.
成立.(2)某药企研制出一种新药,宣称对治疗某种疾病的有效率为
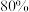 .现随机选择了100名患者,经过使用该药治疗后,治愈的人数为60人,请结合切比雪夫不等式通过计算说明药厂的宣传内容是否真实可信.
.现随机选择了100名患者,经过使用该药治疗后,治愈的人数为60人,请结合切比雪夫不等式通过计算说明药厂的宣传内容是否真实可信.
您最近一年使用:0次
2023-05-27更新
|
3329次组卷
|
13卷引用:吉林省东北师范大学附中2023届高三下学期七模数学试题
吉林省东北师范大学附中2023届高三下学期七模数学试题吉林省长春市东北师范大学附属中学2023届高三第七次模拟考试数学试题(已下线)第四篇 概率与统计 专题4 分赌注问题 微点1 分赌注问题(已下线)高三开学收心考试模拟卷(已下线)第07讲 离散型随机变量的分布列与数字特征(六大题型)(讲义)(已下线)重难点突破01 概率与统计的综合应用(十八大题型)-2广东省佛山市2024届高三上学期教育教学质量检测模拟(一)数学试题陕西省铜川市2024届高三一模数学(理)试题(已下线)随机变量及其分布专题15离散型随机变量的分布列(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大题型)(练习)(已下线)专题6 概率与统计中的新定义压轴大题(过关集训)(已下线)重难点突破03 高等背景下概率论新定义(七大题型)
名校
5 . 我们将服从二项分布的随机变量称为二项随机变量,服从正态分布的随机变量称为正态随机变量.概率论中有一个重要的结论是棣莫弗一拉普拉斯极限定理,它表明,若随机变量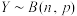 ,当n充分大时,二项随机变量Y可以由正态随机变量X来近似,且正态随机变量X的期望和方差与二项随机变量Y的期望和方差相同.棣莫弗在1733年证明了
,当n充分大时,二项随机变量Y可以由正态随机变量X来近似,且正态随机变量X的期望和方差与二项随机变量Y的期望和方差相同.棣莫弗在1733年证明了 的特殊情形,1812年,拉普拉斯对一般的p进行了证明.现抛掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数超过60次的概率为( )(附:若
的特殊情形,1812年,拉普拉斯对一般的p进行了证明.现抛掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数超过60次的概率为( )(附:若 ,则
,则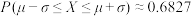 ,
,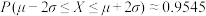 ,
,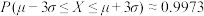 )
)
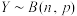 ,当n充分大时,二项随机变量Y可以由正态随机变量X来近似,且正态随机变量X的期望和方差与二项随机变量Y的期望和方差相同.棣莫弗在1733年证明了
,当n充分大时,二项随机变量Y可以由正态随机变量X来近似,且正态随机变量X的期望和方差与二项随机变量Y的期望和方差相同.棣莫弗在1733年证明了 的特殊情形,1812年,拉普拉斯对一般的p进行了证明.现抛掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数超过60次的概率为( )(附:若
的特殊情形,1812年,拉普拉斯对一般的p进行了证明.现抛掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数超过60次的概率为( )(附:若 ,则
,则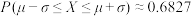 ,
,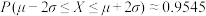 ,
,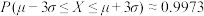 )
)| A.0.1587 | B.0.0228 | C.0.0027 | D.0.0014 |
您最近一年使用:0次
2022-05-13更新
|
2472次组卷
|
21卷引用:福建省厦门市2022届高三毕业班第四次质量检测数学试题
福建省厦门市2022届高三毕业班第四次质量检测数学试题福建省龙岩第一中学2021-2022学年高二下学期第二次月考数学试题(已下线)专题12 四大分布:两点分布、超几何分布、二项分布、正态分布-2021-2022学年高二数学下学期期末必考题型归纳及过关测试(人教A版2019)(已下线)期末押题预测卷04(考试范围:选修二+选修三)-2021-2022学年高二数学下学期期末必考题型归纳及过关测试(人教A版2019)(已下线)8.3 分布列(精练)(已下线)考向43二项分布、正太分布及其应用(重点)-2(已下线)江苏省盐城市、南京市2022届高三上学期1月第一次模拟考试数学试题变式题1-5江西省南昌市第十中学2022-2023学年高二下学期第一次月考数学试题(已下线)第七章 随机变量及其分布 全章总结 (精讲)(3)四川省成都市简阳市阳安中学2023届高三三诊模拟考试数学(理科)试题新疆石河子第一中学2022-2023学年高二下学期5月月考数学试题河北省石家庄市2022-2023学年高二下学期期末数学试题福建省厦门第一中学2022-2023学年高二下学期期末考试数学试题吉林省长春市十一高中2022-2023学年高二下学期期末数学试题陕西省西安市陕西师范大学附属中学渭北中学2023届高三三模理科数学试题河北省石家庄四十一中2022-2023学年高二下学期第二次月考数学试题(已下线)专题04随机变量及其分布(6大考点经典基础练+优选提升练)-【好题汇编】备战2023-2024学年高二数学下学期期末真题分类汇编(新高考专用)广东省江门市新会第一中学2023-2024学年高二下学期期中考试数学试题(已下线)重组10 高二期末真题重组卷(福建卷)B提升卷福建省龙岩市上杭县第一中学2023-2024学年高二下学期数学限时训练试题(十二)广东省珠海市北京师范大学(珠海)附属高级中学2023-2024学年高二下学期6月月考数学试题
解题方法
6 . 为了解顺义区某中学高一年级学生身体素质情况,对高一年级的( )班
)班 (
( )班进行了抽测,采取如下方式抽样:每班随机各抽
)班进行了抽测,采取如下方式抽样:每班随机各抽 名学生进行身体素质监测.经统计,每班
名学生进行身体素质监测.经统计,每班 名学生中身体素质监测成绩达到优秀的人数散点图如下:(
名学生中身体素质监测成绩达到优秀的人数散点图如下:( 轴表示对应的班号,
轴表示对应的班号, 轴表示对应的优秀人数)
轴表示对应的优秀人数) 人,求该生身体素质监测成绩达到优秀的概率;
人,求该生身体素质监测成绩达到优秀的概率;
(2)若从以上统计的高一( )班的
)班的 名学生中抽出
名学生中抽出 人,设
人,设 表示
表示 人中身体素质监测成绩达到优秀的人数,求
人中身体素质监测成绩达到优秀的人数,求 的分布列及其数学期望;
的分布列及其数学期望;
(3)假设每个班学生身体素质优秀的概率与该班随机抽到的 名学生的身体素质优秀率相等.现在从每班中分别随机抽取
名学生的身体素质优秀率相等.现在从每班中分别随机抽取 名同学,用“
名同学,用“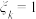 ”表示第
”表示第 班抽到的这名同学身体素质优秀,“
班抽到的这名同学身体素质优秀,“ ”表示第
”表示第 班抽到的这名同学身体素质不是优秀
班抽到的这名同学身体素质不是优秀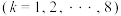 .写出方差
.写出方差 的大小关系(不必写出证明过程).
的大小关系(不必写出证明过程).
 )班
)班 (
( )班进行了抽测,采取如下方式抽样:每班随机各抽
)班进行了抽测,采取如下方式抽样:每班随机各抽 名学生进行身体素质监测.经统计,每班
名学生进行身体素质监测.经统计,每班 名学生中身体素质监测成绩达到优秀的人数散点图如下:(
名学生中身体素质监测成绩达到优秀的人数散点图如下:( 轴表示对应的班号,
轴表示对应的班号, 轴表示对应的优秀人数)
轴表示对应的优秀人数)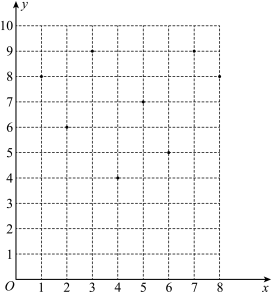
 人,求该生身体素质监测成绩达到优秀的概率;
人,求该生身体素质监测成绩达到优秀的概率;(2)若从以上统计的高一(
 )班的
)班的 名学生中抽出
名学生中抽出 人,设
人,设 表示
表示 人中身体素质监测成绩达到优秀的人数,求
人中身体素质监测成绩达到优秀的人数,求 的分布列及其数学期望;
的分布列及其数学期望;(3)假设每个班学生身体素质优秀的概率与该班随机抽到的
 名学生的身体素质优秀率相等.现在从每班中分别随机抽取
名学生的身体素质优秀率相等.现在从每班中分别随机抽取 名同学,用“
名同学,用“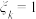 ”表示第
”表示第 班抽到的这名同学身体素质优秀,“
班抽到的这名同学身体素质优秀,“ ”表示第
”表示第 班抽到的这名同学身体素质不是优秀
班抽到的这名同学身体素质不是优秀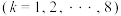 .写出方差
.写出方差 的大小关系(不必写出证明过程).
的大小关系(不必写出证明过程).
您最近一年使用:0次