名校
1 . 设函数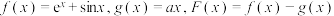 .
.
(1)当 时,求函数
时,求函数 在点
在点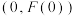 处的切线方程;
处的切线方程;
(2)当 时,设
时,设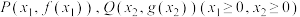 ,且
,且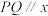 轴,求
轴,求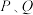 两点间的最短距离;
两点间的最短距离;
(3)若 时,函数
时,函数 的图象恒在
的图象恒在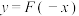 的图象上方,求实数
的图象上方,求实数 的取值范围.
的取值范围.
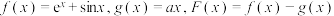 .
.(1)当
 时,求函数
时,求函数 在点
在点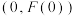 处的切线方程;
处的切线方程;(2)当
 时,设
时,设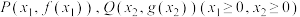 ,且
,且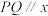 轴,求
轴,求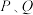 两点间的最短距离;
两点间的最短距离;(3)若
 时,函数
时,函数 的图象恒在
的图象恒在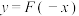 的图象上方,求实数
的图象上方,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
2 . 已知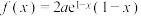 ,其中
,其中 .
.
(1)求 在
在 处的切线方程;
处的切线方程;
(2)若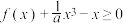 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
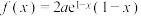 ,其中
,其中 .
.(1)求
 在
在 处的切线方程;
处的切线方程;(2)若
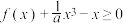 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-27更新
|
439次组卷
|
2卷引用:重庆市西南大学附属中学校2023-2024学年高三上学期期中考试数学试题
名校
解题方法
3 . 已知椭圆 :
: 的焦点分别为
的焦点分别为 ,
, ,过左焦点
,过左焦点 的直线与椭圆交于M,N两点,
的直线与椭圆交于M,N两点, 的周长为
的周长为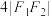 .
.
(1)求椭圆E的离心率;
(2)直线 :
: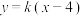 与椭圆有两个不同的交点A,B,直线
与椭圆有两个不同的交点A,B,直线 与x轴的交点为D,若A,B都在x轴上方且点A在线段
与x轴的交点为D,若A,B都在x轴上方且点A在线段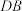 上,O为坐标原点,
上,O为坐标原点,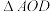 和
和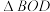 面积分别为
面积分别为 ,
, ,记
,记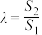 ,当满足条件的实数
,当满足条件的实数 变化时,
变化时, 的取值范围是
的取值范围是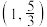 ,求椭圆E的方程.
,求椭圆E的方程.
 :
: 的焦点分别为
的焦点分别为 ,
, ,过左焦点
,过左焦点 的直线与椭圆交于M,N两点,
的直线与椭圆交于M,N两点, 的周长为
的周长为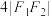 .
.(1)求椭圆E的离心率;
(2)直线
 :
: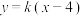 与椭圆有两个不同的交点A,B,直线
与椭圆有两个不同的交点A,B,直线 与x轴的交点为D,若A,B都在x轴上方且点A在线段
与x轴的交点为D,若A,B都在x轴上方且点A在线段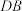 上,O为坐标原点,
上,O为坐标原点,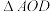 和
和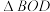 面积分别为
面积分别为 ,
, ,记
,记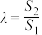 ,当满足条件的实数
,当满足条件的实数 变化时,
变化时, 的取值范围是
的取值范围是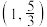 ,求椭圆E的方程.
,求椭圆E的方程.
您最近一年使用:0次
名校
解题方法
4 . 已知双曲线 上的一点到两条渐近线的距离之积为2且双曲线C的离心率为
上的一点到两条渐近线的距离之积为2且双曲线C的离心率为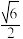 .
.
(1)求双曲线C的方程;
(2)已知M是直线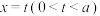 上一点,直线
上一点,直线 交双曲线C于A(A在第一象限),B两点,O为坐标原点,过点M作直线
交双曲线C于A(A在第一象限),B两点,O为坐标原点,过点M作直线 的平行线l,l与直线
的平行线l,l与直线 交于点P,与x轴交于点Q,若P为线段
交于点P,与x轴交于点Q,若P为线段 的中点,求实数t的值.
的中点,求实数t的值.
 上的一点到两条渐近线的距离之积为2且双曲线C的离心率为
上的一点到两条渐近线的距离之积为2且双曲线C的离心率为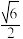 .
.(1)求双曲线C的方程;
(2)已知M是直线
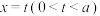 上一点,直线
上一点,直线 交双曲线C于A(A在第一象限),B两点,O为坐标原点,过点M作直线
交双曲线C于A(A在第一象限),B两点,O为坐标原点,过点M作直线 的平行线l,l与直线
的平行线l,l与直线 交于点P,与x轴交于点Q,若P为线段
交于点P,与x轴交于点Q,若P为线段 的中点,求实数t的值.
的中点,求实数t的值.
您最近一年使用:0次
2023-11-14更新
|
894次组卷
|
3卷引用:重庆市南岸区四川外语学院重庆第二外国语学校2024届高三上学期期中数学试题
5 . 已知函数 .
.
(1)若函数 是减函数,求
是减函数,求 的取值范围;
的取值范围;
(2)若 有两个零点
有两个零点 ,且
,且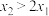 ,证明:
,证明: .
.
 .
.(1)若函数
 是减函数,求
是减函数,求 的取值范围;
的取值范围;(2)若
 有两个零点
有两个零点 ,且
,且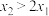 ,证明:
,证明: .
.
您最近一年使用:0次
名校
6 . 已知函数 ,
, .
.
(1)若 ,证明:当
,证明:当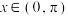 时,
时,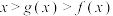 ;
;
(2)当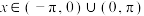 时,
时,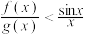 ,求
,求 的取值范围.
的取值范围.
 ,
, .
.(1)若
 ,证明:当
,证明:当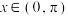 时,
时,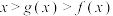 ;
;(2)当
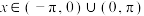 时,
时,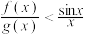 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-10-31更新
|
596次组卷
|
5卷引用:重庆市名校联盟2024届高三上学期期中数学试题
重庆市名校联盟2024届高三上学期期中数学试题重庆市云阳县实验中学2024届高三上学期11月检测数学试题重庆市九龙坡区育才中学校2024届高三上学期第三次联考复习数学试题(已下线)第九章 导数与三角函数的联袂 专题三 含三角函数的恒成立问题 微点1 三角函数的恒成立问题(一)(已下线)第九章 导数与三角函数的联袂 专题三 含三角函数的恒成立问题 微点3 三角函数的恒成立问题(三)
名校
7 . 已知函数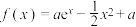 有两个不同的极值点
有两个不同的极值点 .
.
(1)求实数 的取值范围;
的取值范围;
(2)已知 ,且
,且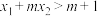 ,求
,求 的取值范围.
的取值范围.
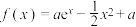 有两个不同的极值点
有两个不同的极值点 .
.(1)求实数
 的取值范围;
的取值范围;(2)已知
 ,且
,且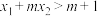 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-10-29更新
|
635次组卷
|
3卷引用:重庆市第八中学校2024届高三上学期10月期中数学试题
名校
8 . 已知函数
(1)若 ,证明:
,证明: 在
在 上恒成立;
上恒成立;
(2)若方程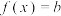 有两个实数根
有两个实数根 且
且 ,证明:
,证明:


(1)若
 ,证明:
,证明: 在
在 上恒成立;
上恒成立;(2)若方程
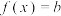 有两个实数根
有两个实数根 且
且 ,证明:
,证明:

您最近一年使用:0次
2023-10-29更新
|
587次组卷
|
3卷引用:重庆市南岸区四川外语学院重庆第二外国语学校2024届高三上学期期中数学试题
名校
解题方法
9 . 已知函数 ,
, .
.
(1)若 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(2)当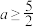 时,证明:
时,证明: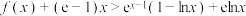 .
.
 ,
, .
.(1)若
 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;(2)当
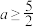 时,证明:
时,证明: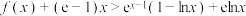 .
.
您最近一年使用:0次
2023-10-27更新
|
678次组卷
|
7卷引用:重庆市北碚区西南大学附属中学校2024届高三上学期11月期中数学试题
重庆市北碚区西南大学附属中学校2024届高三上学期11月期中数学试题河北省邢台市五岳联盟2024届高三上学期第四次月考数学试题河南省周口市项城市正泰博文高级中学2023-2024学年高三上学期10月月考数学试题河北省保定市部分高中2024届高三上学期10月联考数学试题河南省名校联盟2024届高三上学期11月段考数学试题(已下线)模块三 大招25 不等式证明——指对处理(已下线)模块三 大招6 不等式证明——指对处理
名校
解题方法
10 . 已知椭圆 的左右顶点分别为A,B,椭圆E与抛物线
的左右顶点分别为A,B,椭圆E与抛物线 的准线相切,椭圆的左焦点F到A,B两点的距离之积为3.
的准线相切,椭圆的左焦点F到A,B两点的距离之积为3.
(1)求椭圆E的方程;
(2)过点 作斜率为k的直线与椭圆E交于不同的两点P,Q,直线BP,BQ分别与y轴交于点M,N,则
作斜率为k的直线与椭圆E交于不同的两点P,Q,直线BP,BQ分别与y轴交于点M,N,则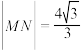 ,求直线PQ的方程.
,求直线PQ的方程.
 的左右顶点分别为A,B,椭圆E与抛物线
的左右顶点分别为A,B,椭圆E与抛物线 的准线相切,椭圆的左焦点F到A,B两点的距离之积为3.
的准线相切,椭圆的左焦点F到A,B两点的距离之积为3.(1)求椭圆E的方程;
(2)过点
 作斜率为k的直线与椭圆E交于不同的两点P,Q,直线BP,BQ分别与y轴交于点M,N,则
作斜率为k的直线与椭圆E交于不同的两点P,Q,直线BP,BQ分别与y轴交于点M,N,则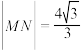 ,求直线PQ的方程.
,求直线PQ的方程.
您最近一年使用:0次
2023-09-29更新
|
705次组卷
|
2卷引用:重庆市北碚区西南大学附属中学校2024届高三上学期11月期中数学试题



