名校
1 . 王昌龄是盛唐著名的边塞诗人,被誉为“七绝圣手”,其诗作《从军行》中的诗句“青海长云暗雪山,孤城遥望玉门关.黄沙百战穿金甲,不破楼兰终不还”传诵至今.由此推断,其中最后一句“返回家乡”是“攻破楼兰”的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
2022-11-14更新
|
3008次组卷
|
92卷引用:湖南省永州市2020-2021学年高一上学期期末数学试题
湖南省永州市2020-2021学年高一上学期期末数学试题(已下线)第5讲常用逻辑概念-【A+课堂】2021-2022学年高一数学同步精讲精练(沪教版2020必修第一册)(已下线)专练05 充分条件与必要条件-2021-2022学年高一数学上册同步课后专练(人版A版必修第一册)(已下线)【师说智慧课堂】新教材必修一第一章集合与逻辑用语章末检测试-2021-2022学年高中数学新教材同步练习(已下线)1.4 (整合练)充分条件与必要条件-2021-2022学年高中数学必修第一册课时解读与训练(人教A版2019)(已下线)1.4 (分层练)充分条件与必要条件-2021-2022学年高中数学必修第一册课时解读与训练(人教A版2019)(已下线)1.4 充分条件与必要条件(备作业)-【上好课】2021-2022学年高一数学同步备课系列(人教A版2019必修第一册)湖北省武汉市洪山高级中学2021-2022学年高一上学期第一次月考数学试题山东省烟台市牟平第一中学2021-2022学年高一上学期10月月考数学试题重庆市长寿中学校2021-2022学年高一上学期10月月考数学试题2017届山西省高三下学期名校联考数学(文)试卷江西省赣州市红色七校2017-2018届高三第一次联考数学(文)试题山西省太原市太原十二中2017-2018学年高二上学期第二次月考数学(文)试题【全国百强校】黑龙江省大庆实验中学2018-2019学年高二上学期期中考试数学(文)试题【市级联考】河南省豫西名校2018-2019学年高二上学期第二次联考数学(文)试卷【全国百强校】宁夏银川一中2019届高三第五次月考数学(文)试题【全国百强校】甘肃省兰州市第一中学2018-2019学年高二上学期期末考试数学(文)试题【全国百强校】甘肃省兰州第一中学2018-2019学年高二上学期期末考试数学(理)试题【市级联考】江西省鹰潭市2018-2019学年高二上学期期末质量检测数学(理)试题【省级联考】豫西名校2018-2019学年高二上学期第二次联考文数试题新疆奎屯市第一高级中学2018-2019学年高二下学期期末考试数学(文)试题人教A版 新教材 必修第一册1.4 充分条件与必要条件同步训练人教B版(2019) 必修第一册 过关斩将 第一章 1.2 综合拔高练上海市上海中学2019-2020学年高三上学期期中数学试题辽宁省朝阳市朝阳县柳城高中2019-2020学年高一上学期期中数学试题贵州省安顺市普通高中2018-2019学年高二上学期期末考试数学(理)试题宁夏石嘴山市第三中学2019-2020学年高二上学期期末考试数学(理)试题宁夏中卫市海原县第一中学2019-2020学年高二上学期期末数学(文)试题2020届福建省莆田第二十五中学高三上学期期末数学(文)试题人教B版(2019) 必修第一册 逆袭之路 第一章 1.2 常用逻辑用语 1.2.3 充分条件、必要条件人教A版(2019) 必修第一册 逆袭之路 第一章 1.4 充分条件与必要条件山东省泰安市泰安一中2019-2020学年高一上学期期中数学试题安徽省合肥市第一中学2019-2020学年高二上学期期末数学(文)试题贵州省思南中学2019-2020学年高二上学期期末考试数学(文)试题贵州省思南中学2019-2020学年高二上学期期末考试数学(理)试题山西省吕梁市离石区2018-2019学年高二下学期期末数学(文)试题江苏省常州市前黄高级中学2019-2020学年高二上学期期末数学试题2017届陕西省榆林市高三第二次模拟测试数学(文)试题浙江省温州市乐清乐成寄宿中学2017-2018学年高三上学期期中数学试题(已下线)第一章 2.1 第1课时 必要条件与充分条件-【新教材】北师大版(2019)高中数学必修第一册练习(已下线)专题1.2 命题及其关系、充分条件与必要条件(精练)-2021年高考数学(文)一轮复习学与练(已下线)1.4充分条件与必要条件-2020-2021学年新教材名师导学导练高中数学必修第一册(人教A版)(已下线)1.4充分条件与必要条件-【新教材】人教(A)版高中数学必修第一册限时作业湖北省潜江市文昌中学2019-2020学年高三上学期期末数学试题(已下线)山西省2017届高三下学期名校联考数学(文)试题江苏省扬州市宝应县2020-2021学年高三上学期初调研测试数学试题陕西省西安交大附中2019-2020学年高二上学期期末文科数学试题上海奉贤区致远高级中学2020-2021学年高一上学期10月月考数学试题江苏省徐州市沛县2020-2021学年高一上学期第一次学情调研数学试题福建省泉州实验中学2020-2021学年高一上学期第一阶段考试数学试题山西省怀仁市2020-2021学年高一上学期期中数学试题山东省济宁市兖州区2020-2021学年高一上学期期中考试数学试题江苏省无锡市江阴市青阳高级中学2020-2021学年高一上学期12月阶段检测数学试题江苏省苏州大学附属中学2020-2021学年高二上学期期末复习测试一数学试题广东省佛山市第三中学2020-2021学年高一上学期第一次月考数学试题江苏省南京市金陵中学河西分校2020-2021学年高一上学期阶段检测数学试题浙江省杭州市淳安县汾口中学2020-2021学年高一上学期10月月考数学试题2020届湖北省华中师范大学第一附属中学高三下学期月考理科数学试题湖南省长沙市雨花区2021-2022学年高一上学期期末数学试题广东省广州大学附属中学等三校2021-2022学年高二上学期期末联考数学试题广东省广州大学附属中学2021-2022学年高二上学期期末数学试题(已下线)1.2 逻辑用语与充分、必要条件(精练)-【一隅三反】2023年高考数学一轮复习(基础版)(新高考地区专用)(已下线)1.4充分条件与必要条件C卷章节综合测试-集合与常用逻辑用语(已下线)1.2.3 充分条件、必要条件江苏省南京市第二十九中学2022-2023学年高一上学期10月学情调研测试数学试题 湘鄂冀三省益阳平高学校、长沙市平高中学等七校2022-2023学年高一上学期10月联考数学试题湖北省鄂州市鄂城区秋林高级中学2022-2023学年高一上学期10月月考数学试题宁夏银川市二十四中学2022-2023学年高一上学期第一次月考数学试题广东省佛山市顺德区郑裕彤中学2022-2023学年高一上学期第一次段考数学试题广东省佛山市顺德区乐从中学2022-2023学年高一上学期期中数学试题浙江省温州市苍南县树人中学2020-2021学年高一上学期9月月考数学试题 重庆市云阳高级中学校2022-2023学年高一上学期第三次质量检测数学试题黑龙江省哈尔滨市宾县第二中学2021-2022学年高一上学期期末数学试题(已下线)第一章 集合与常用逻辑用语 讲核心(已下线)第04讲 充分条件与必要条件-【暑假自学课】(人教A版2019必修第一册)四川省射洪中学校2022-2023学年高一上学期10月第一次月测数学试题辽宁省大连市第八中学2023届高考适应性测试数学试题1.4.2 充要条件练习(已下线)第04讲 1.4充分条件与必要条件(1)-【帮课堂】(已下线)1.4 充分必要条件(精练)-《一隅三反》(已下线)1.4 充分条件与必要条件(5大题型)精讲-【题型分类归纳】(已下线)2.2 充分条件、必要条件、充要条件(5大题型)-【题型分类归纳】(苏教版2019必修第一册)(已下线)第1章 集合与常用逻辑用语(基础、典型、新文化、压轴)分类专项训练甘肃省天水市甘谷县第二中学2023-2024学年高三上学期10月月考数学试题(已下线)第02讲 常用逻辑用语(练透6大重点题型)-【练透核心考点】(已下线)第一章 集合与常用逻辑用语(知识归纳+7类题型突破)-速记·巧练(人教A版2019必修第一册)湖北省恩施州咸丰春晖教育集团2023-2024学年高一上学期期中数学试题(已下线)1.4.2 充要条件——课后作业(基础版)江苏省镇江市实验高级中学2023-2024学年高一上学期学情调研(9月)数学试卷四川省南充市阆中中学校2024-2025学年高一上学期9月检测数学试题福建省泉州市安溪俊民中学2024-2025学年高一上学期第一次月考数学试卷
名校
解题方法
2 . 在 九章算术
九章算术 中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑
中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑 中,
中, 平面BCD,
平面BCD, ,且
,且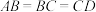 ,M为AD的中点,则异面直线BM与CD夹角的余弦值为( )
,M为AD的中点,则异面直线BM与CD夹角的余弦值为( )
 九章算术
九章算术 中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑
中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑 中,
中, 平面BCD,
平面BCD, ,且
,且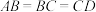 ,M为AD的中点,则异面直线BM与CD夹角的余弦值为( )
,M为AD的中点,则异面直线BM与CD夹角的余弦值为( )A.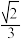 | B. | C. | D.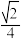 |
您最近一年使用:0次
2022-10-27更新
|
2318次组卷
|
33卷引用:第一章 空间向量与立体几何单元检测(知识达标卷)-【一堂好课】2021-2022学年高二数学上学期同步精品课堂(人教A版2019选择性必修第一册)
(已下线)第一章 空间向量与立体几何单元检测(知识达标卷)-【一堂好课】2021-2022学年高二数学上学期同步精品课堂(人教A版2019选择性必修第一册)(已下线)专练7 用空间向量研究距离、夹角问题-2021-2022学年高二数学上册同步课后专练(人版A版选择性必修第一册)(已下线)专题8.1 与数学文化相关的数学考题-玩转压轴题,进军满分之2021高考数学选择题填空题广东省佛山市顺德区文德学校2021-2022学年高二上学期第一次阶段测试数学试题苏教版(2019) 选修第二册 名师精选 第六章 空间向量与立体几何人教A版(2019) 选修第一册 实战演练 第一章 课时练习 09 用空间向量研究距离、夹角问题山东省潍坊市(高密一中、高密三中、高密四中)2021-2022学年高二12月月考数学试题【市级联考】安徽省黄山市2019届高三第二次质量检测数学(理)试题【市级联考】安徽省黄山市2019届高三毕业班第二次质量检测数学(文)试题2【市级联考】安徽省黄山市2019届高三毕业班第二次质量检测数学(文)试题12019年10月黑龙江省哈尔滨市第六中学第二次调研考试数学(文)试题人教B版(2019) 必修第四册 过关斩将 第十一章 立体几何初步 本章达标检测辽宁省辽河油田第二高级中学2020-2021学年高二10月月考数学试题沪教版(2020) 选修第一册 单元训练 第3章 空间向量在立体几何体中的应用(A卷)(已下线)第02讲 基本图形的位置关系(1)河南省鹤壁市浚县浚县第一中学2021-2022学年高一下学期7月月考数学试题空间向量的应用(已下线)第02讲 空间点、直线、平面之间的位置关系 (精讲)-22023版 湘教版(2019) 选修第二册 过关斩将 第2章 2.4.3 向量与夹角辽宁省沈阳市郊联体2022-2023学年上学期高二年级10月数学月考试题黑龙江省哈尔滨市第二十四中学校2022-2023学年高二上学期10月月考数学试题辽宁省沈阳市五校协作体2022-2023学年高二上学期期中数学试题湖南省衡阳师范学院祁东附属中学2022-2023学年高二上学期期中数学试题上海市延安中学2021-2022学年高二下学期期中数学试题(已下线)模块五 空间向量与立体几何-1第三章空间向量与立体几何 单元练习-2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册浙江省温州市乐清市知临中学2022-2023学年高一下学期期中数学试题第一章 空间向量与立体几何 (练基础)(已下线)第一章 空间向量与立体几何(基础、典型、新文化、压轴)分类专项训练四川省绵阳南山中学实验学校2023-2024学年高二上学期9月月考数学试题福建省连江黄如论中学六校联考2023-2024学年高二上学期期中数学试题(已下线)第一章 空间向量与立体几何(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第一册)(已下线)模块一 专题6《 空间向量应用》 A基础卷 (苏教版)
名校
3 . 设计如图所示的四个电路图, :“开关
:“开关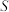 闭合”,
闭合”, :“灯泡
:“灯泡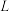 亮”,则
亮”,则 是
是 的充要条件的电路图是( )
的充要条件的电路图是( )
 :“开关
:“开关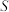 闭合”,
闭合”, :“灯泡
:“灯泡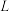 亮”,则
亮”,则 是
是 的充要条件的电路图是( )
的充要条件的电路图是( )A.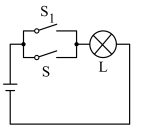 | B. |
C.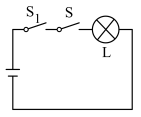 | D.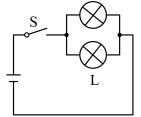 |
您最近一年使用:0次
2022-08-27更新
|
1737次组卷
|
30卷引用:专题01 与集合、常用逻辑用语相关的情景化试题 - 2021-2022学年高一数学新教材情境化新题(人教A版2019必修第一册)
(已下线)专题01 与集合、常用逻辑用语相关的情景化试题 - 2021-2022学年高一数学新教材情境化新题(人教A版2019必修第一册)(已下线)【课时作业】1.4 充分条件与必要条件-2021-2022学年高一数学《新教材同步精典导学案》(人教A版2019必修第一册)(已下线)课时1.4 (考点讲解)充分条件和必要条件-2021-2022学年高一数学新课学习讲与练精品资源(人教版2019必修第一册)广东省广州市第四中学2021-2022学年高一上学期10月月考数学试题山东省菏泽市郓城县郓城第一中学2021-2022学年高一上学期10月月考数学试题黑龙江省双鸭山市第一中学2021-2022学年高一上学期期中数学试题苏教版(2019) 必修第一册 过关检测 第2章 2.2充分条件、必要条件、充要条件(2)江苏省常州市金坛区2021-2022学年高一上学期期中数学试题第2章 常用逻辑用语(章末测试提高卷)-2021-2022学年高一数学同步单元测试定心卷(苏教版2019必修第一册)人教B版(2019) 必修第一册 必杀技 第一章 1.2.3课时2 充要条件人教A版(2019) 必修第一册 必杀技 第一章 1.4.2 充要条件(已下线)专题01 集合与简易逻辑-备战2020年新高考数学新题型之【多选题】-《2020年新高考政策解读与配套资源》(已下线)专题1.4 充分条件与必要条件-2020-2021学年高一数学尖子生同步培优题典(人教A版2019必修第一册)江苏省无锡市江阴市第二中学2020-2021学年高一上学期12月质量检测数学试题江苏省连云港市赣榆智贤中学2020-2021学年高二上学期12月月考数学试题江苏省宿迁市泗洪县洪翔中学2020-2021学年高二上学期数学期中模拟试题广东省揭阳市揭东区2021-2022学年高一上学期期末数学试题2023版 苏教版(2019) 必修第一册 名校名师卷 第二单元 常用逻辑用语2023版 湘教版(2019) 必修第一册 名师精选卷 第二单元 常用逻辑用语甘肃省临夏州临夏县中学2022-2023学年高一上学期9月月考数学试题黑龙江省哈尔滨市宾县第二中学2022-2023学年高一上学期第二次月考数学试题江苏省苏州市吴江汾湖高级中学2022-2023学年高一上学期9月教学调研测试数学试题贵州省贵阳市第一中学2022-2023学年高一上学期第一次摸底考试数学试题(已下线)专题1-2 简易逻辑(讲+练)-2辽宁省沈阳市东北育才学校高中部2022-2023学年高一上学期开学摸底考试数学试题青海省西宁市海湖中学2022-2023学年高一上学期期末数学试题(已下线)第06讲 充分条件、必要条件、充要条件-【暑假自学课】(苏教版2019必修第一册)(已下线)模块二 专题1《集合与常用逻辑用语》单元检测篇 A基础卷 (人教A)【课后练】 1.2.2 充分条件和必要条件课后作业-湘教版(2019)必修(第一册)第1章 集合与逻辑贵州省毕节市金沙县第五中学2024-2025学年高一上学期第一次月考数学试题
名校
解题方法
4 . 明朝的一个葡萄纹椭圆盘如图(1)所示,清朝的一个青花山水楼阁纹饰椭圆盘如图(2)所示,北宋的一个汝窑椭圆盘如图(3)所示,这三个椭圆盘的外轮廓均为椭圆.已知图(1)、(2)、(3)中椭圆的长轴长与短轴长的比值分别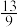 、
、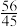 、
、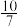 ,设图(1)、(2)、(3)中椭圆的离心率分别为
,设图(1)、(2)、(3)中椭圆的离心率分别为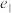 、
、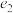 、
、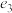 ,则( )
,则( )
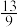 、
、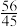 、
、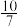 ,设图(1)、(2)、(3)中椭圆的离心率分别为
,设图(1)、(2)、(3)中椭圆的离心率分别为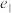 、
、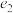 、
、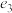 ,则( )
,则( )
A.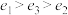 | B.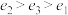 |
C. | D.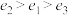 |
您最近一年使用:0次
2021-05-09更新
|
2864次组卷
|
30卷引用:云南、贵州、四川、广西四省2021届高三5月模拟联考数学(理)试题
云南、贵州、四川、广西四省2021届高三5月模拟联考数学(理)试题福建省莆田市2021届高三三模数学试卷湖南省部分学校2021届高三下学期联考数学试题宁夏银川市第二中学2021届高三下学期二模数学(文)试题宁夏银川市第二中学2021届高三二模数学(理)试题山西省晋城市2021届高三三模数学(理)试题山西省晋城市2021届高三三模数学(文)试题广西2021届高三5月联考数学(文)试题吉林省白山市2021届高三三模联考数学(文科)试题吉林省白山市2021届高三三模联考数学(理科)试题山东省2021届高三5月联考数学试题广东省肇庆市百花中学2021届高三下学期5月模拟数学试题安徽省蚌埠市第二中学2021届高三下学期高考最后一模文科数学试题辽宁省朝阳市2021届高三高考数学三模试题吉林省白山市2021届高三第四次联考数学(理)试题广西玉林市育才中学2021届高三5月三模数学(文)试题山东省泰安市与济南市章丘区2021届高三5月联合模拟考试数学试题山东省2021届高三5月份高考数学联考试题甘肃省白银市靖远县2021届高三第四次联考数学(理)试题甘肃省白银市靖远县2021届高三第四次联考数学(文)试题江苏省宿迁市泗阳县实验高级中学2021-2022学年高二上学期第一次质量调研数学试题(已下线)专练34 专题强化6-椭圆的综合应用-2021-2022学年高二数学上册同步课后专练(人版A版选择性必修第一册)(已下线)2022届高三普通高等学校招生全国统一考试数学信息卷(七)河北省张家口第一中学2021-2022学年高二上学期期中数学试题(已下线)第29节 椭圆(已下线)一轮复习适应训练卷(4)-2022年暑假高二升高三数学一轮复习适应训练卷(全国通用)2023版 苏教版(2019) 选修第一册 突围者 第3章 第一节 课时2 椭圆的几何性质河北师范大学附属实验中学2022-2023学年高二上学期阶段测试(线上)数学试题第3章 椭圆方程及性质(基础卷)-【满分计划】2022-2023学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)(已下线)第五节 椭圆 第一课时 椭圆的定义、方程与性质 讲
名校
5 . 《九章算术》是古代中国乃至东方的第一部自成体系的数学专著,书中记载了一种名为“刍甍”的五面体(如图),其中四边形 为矩形,
为矩形,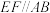 ,若
,若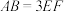 ,
, 和
和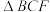 都是正三角形,且
都是正三角形,且 ,则异面直线
,则异面直线 与
与 所成角的大小为( )
所成角的大小为( )
 为矩形,
为矩形,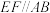 ,若
,若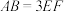 ,
, 和
和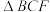 都是正三角形,且
都是正三角形,且 ,则异面直线
,则异面直线 与
与 所成角的大小为( )
所成角的大小为( )
A. | B.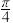 | C. | D.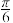 |
您最近一年使用:0次
2021-01-03更新
|
2054次组卷
|
11卷引用:专题02 空间向量与立体几何的典型题(二)-【尖子生专用】2021-2022学年高二数学考点培优训练(人教A版2019选择性必修第一册)
(已下线)专题02 空间向量与立体几何的典型题(二)-【尖子生专用】2021-2022学年高二数学考点培优训练(人教A版2019选择性必修第一册)吉林省长春市东北师范大学附属中学2021-2022学年高二上学期10月阶段考试数学(理)试题江苏省无锡市江阴高级中学2021-2022学年高二上学期期中数学试题山西省运城市高中联合体2020-2021学年高二上学期12月调研测试数学(理)试题2023版 北师大版(2019) 选修第一册 名师精选卷 第三章 空间向量与立体几何广东省珠海市第二中学2022-2023学年高二上学期10月月考数学试题黑龙江省齐齐哈尔市普高联谊校2022-2023学年高二上学期期中数学试题吉林省长春市新解放学校2022-2023学年高二上学期11月月考数学试题人教A版(2019) 选修第一册 第一章 空间向量与立体几何 章末达标检测卷人教A版(2019) 选修第一册 数学奇书 第一章 空间向量与立体几何 章末整合提升山东省淄博第五中学2024-2025学年高二上学期10月月考数学试题
名校
6 . 阿基米德是古希腊著名的数学家、物理学家,他利用“逼近法”得到椭圆的面积除以圆周率 等于椭圆的长半轴长与短半轴长的乘积,已知在平面直角坐标系
等于椭圆的长半轴长与短半轴长的乘积,已知在平面直角坐标系 中,椭圆
中,椭圆 的面积为
的面积为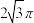 ,两焦点与短轴的一个端点构成等边三角形,则椭圆
,两焦点与短轴的一个端点构成等边三角形,则椭圆 的标准方程是( )
的标准方程是( )
 等于椭圆的长半轴长与短半轴长的乘积,已知在平面直角坐标系
等于椭圆的长半轴长与短半轴长的乘积,已知在平面直角坐标系 中,椭圆
中,椭圆 的面积为
的面积为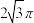 ,两焦点与短轴的一个端点构成等边三角形,则椭圆
,两焦点与短轴的一个端点构成等边三角形,则椭圆 的标准方程是( )
的标准方程是( )A. | B. | C.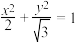 | D. |
您最近一年使用:0次
2021-09-24更新
|
2137次组卷
|
11卷引用:北师大版(2019) 选修第一册 突围者 第二章 全章综合检测
北师大版(2019) 选修第一册 突围者 第二章 全章综合检测(已下线)专题9.3 椭圆 2022年高考数学一轮复习讲练测(新教材新高考)(讲)福建省莆田第一中学2021-2022学年高二上学期期中考试数学试题浙江省嘉兴市海盐第二高级中学2021-2022学年高二上学期10月阶段检测数学试题(已下线)9.3 椭圆(精练)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)辽宁省大连市第八中学2021-2022学年高二上学期期末考试数学试题2023版 北师大版(2019) 选修第一册 突围者 第二章 全章综合检测(已下线)9.2 椭圆(精讲)第三章 圆锥曲线的方程单元测试(巅峰版)-【新教材优创】突破满分数学之2022-2023学年高二数学重难点突破+课时训练 (人教A版2019选择性必修第一册)河北省衡水市第二中学2024-2025学年高二上学期9月月考数学试题山东省郓城第一中学2024-2025学年高二上学期10月月考数学试题
名校
解题方法
7 . 著名的天文学家、数学家约翰尼斯·开普勒(Johannes Kepler)发现了行星运动三大定律,其中开普勒第一定律又称为轨道定律,即所有行星绕太阳运动的轨道都是椭圆,且太阳处在椭圆的一个焦点上.记地球绕太阳运动的轨道为椭圆C,在地球绕太阳运动的过程中,若地球与太阳的最远距离与最近距离之比为 ,则C的离心率为( )
,则C的离心率为( )
 ,则C的离心率为( )
,则C的离心率为( )A. | B. | C. | D.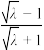 |
您最近一年使用:0次
2021-09-17更新
|
2095次组卷
|
12卷引用:广东省深圳市罗湖区2022届高三上学期第一次质量检测数学试题
广东省深圳市罗湖区2022届高三上学期第一次质量检测数学试题湖北省黄石市大冶市第一中学2021-2022学年高二上学期10月月考数学试题(已下线)数学与数学家辽宁省大连市第八中学2021-2022学年高二上学期期中考试数学试题(已下线)第十一章 圆锥曲线专练3—椭圆的离心率1-2022届高三数学一轮复习(已下线)专题16 椭圆(选择题、填空题)-备战2022年高考数学(文)母题题源解密(全国甲卷)(已下线)专题41 离心率的求值或取值范围问题-学会解题之高三数学万能解题模板【2022版】(已下线)专题1 椭圆-学会解题之高三数学321训练体系【2022版】3.5圆锥曲线的应用 同步练习甘肃省张掖市某重点校2023-2024学年高二上学期9月月考数学试题湖南省长沙市师大思沁高级中学2022-2023学年高二上学期期中考试数学试卷【课后练】 3.5 圆锥曲线的应用 课后作业-湘教版(2019)选择性必修第一册 第3章 圆锥曲线与方程
名校
8 . 历史上第一个研究圆锥曲线的是梅纳库莫斯(公元前375年—325年),大约100年后,阿波罗尼奥斯更详尽、系统地研究了圆锥曲线,并且他还进一步研究了这些圆锥曲线的光学性质,比如:从抛物线的焦点发出的光线或声波在经过抛物线反射后,反射光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的光线,经抛物线反射后,反射光线经过抛物线的焦点.设抛物线 :
: ,一束平行于抛物线对称轴的光线经过
,一束平行于抛物线对称轴的光线经过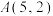 ,被抛物线反射后,又射到抛物线
,被抛物线反射后,又射到抛物线 上的
上的 点,则
点,则 点的坐标为( )
点的坐标为( )
 :
: ,一束平行于抛物线对称轴的光线经过
,一束平行于抛物线对称轴的光线经过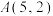 ,被抛物线反射后,又射到抛物线
,被抛物线反射后,又射到抛物线 上的
上的 点,则
点,则 点的坐标为( )
点的坐标为( )A.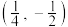 | B. | C.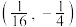 | D.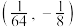 |
您最近一年使用:0次
2021-04-10更新
|
1904次组卷
|
4卷引用:东北三省四城市联考暨沈阳市2021届高三质量监测(二)数学试题
东北三省四城市联考暨沈阳市2021届高三质量监测(二)数学试题(已下线)押第11题 抛物线-备战2021年高考数学(理)临考题号押题(全国卷1)(已下线)专题25 圆锥曲线的光学性质及其应用 微点3 抛物线的光学性质及其应用陕西师范大学附属中学2022-2023学年高三上学期期中理科数学试题
名校
9 . 如图,正方形内的图形来自中国古代的太极图.勤劳而充满智慧的我国古代劳动人民曾用太极图解释宇宙现象.太极图由正方形的内切圆(简称大圆)和两个互相外切且半径相等的圆(简称小圆)的半圆弧组成,两个小圆与大圆均内切.若正方形的边长为8,则以两个小圆的圆心(图中两个黑白点视为小圆的圆心)为焦点,正方形对角线所在直线为渐近线的双曲线实轴长是_______ .

您最近一年使用:0次
2021-01-14更新
|
1770次组卷
|
11卷引用:2021年1月浙江省普通高中学业水平考试数学试题
2021年1月浙江省普通高中学业水平考试数学试题(已下线)专题15 双曲线(客观题)-2021年高考数学(理)二轮复习热点题型精选精练(已下线)专题14 双曲线(客观题)-2021年高考数学二轮复习热点题型精选精练(新高考地区专用)(已下线)专题14 双曲线(客观题)-2021年高考数学(文)二轮复习热点题型精选精练第三章 (综合培优)圆锥曲线的方程 B卷-【双基双测】2021-2022学年高二数学同步单元AB卷(浙江专用)(人教A版2019选择性必修第一册)苏教版(2019) 选修第一册 选填专练 第3章 限时小练19 双曲线的几何性质(已下线)第3章 圆锥曲线的方程 章末测试(基础)-2021-2022学年高二数学一隅三反系列(人教A版2019选择性必修第一册)(已下线)第30节 双曲线新疆奇台县第一中学2022-2023学年高二上学期期中考试数学试题甘肃省兰州第一中学2022-2023学年高二上学期期末考试数学试题天津市第一中学2024-2025学年高二上学期期中质量调查数学试题
名校
解题方法
10 . 十七世纪法国数学家费马在《平面与立体轨迹引论》中证明,方程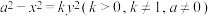 表示椭圆,费马所依据的是椭圆的重要性质:若从椭圆上任意一点P(异于A,B两点)向长轴AB引垂线,垂足为Q,记
表示椭圆,费马所依据的是椭圆的重要性质:若从椭圆上任意一点P(异于A,B两点)向长轴AB引垂线,垂足为Q,记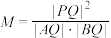 .下列说法正确的是( )
.下列说法正确的是( )
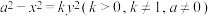 表示椭圆,费马所依据的是椭圆的重要性质:若从椭圆上任意一点P(异于A,B两点)向长轴AB引垂线,垂足为Q,记
表示椭圆,费马所依据的是椭圆的重要性质:若从椭圆上任意一点P(异于A,B两点)向长轴AB引垂线,垂足为Q,记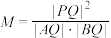 .下列说法正确的是( )
.下列说法正确的是( )| A.M的值与Р点在椭圆上的位置有关 | B.M的值与Р点在椭圆上的位置无关 |
| C.M的值越大,椭圆的离心率越大 | D.M的值越大,椭圆的离心率越小 |
您最近一年使用:0次
2021-10-18更新
|
1721次组卷
|
9卷引用:辽宁省沈阳市沈阳市第一二〇中学2021-2022学年高二上学期第二次质量检测数学试题
辽宁省沈阳市沈阳市第一二〇中学2021-2022学年高二上学期第二次质量检测数学试题(已下线)数学与数学家(已下线)专题3.4 椭圆的简单几何性质-重难点题型检测-2021-2022学年高二数学举一反三系列(人教A版2019选择性必修第一册)辽宁省大连市第八中学2021-2022学年高二上学期期中考试数学试题(已下线)第十一章 圆锥曲线专练1—椭圆小题1-2022届高三数学一轮复习(已下线)考点19 圆锥曲线-2022年高考数学一轮复习小题多维练(新高考版)(已下线)专题11 费马甘肃省张掖市某重点校2023-2024学年高二上学期9月月考数学试题江西省南昌市豫章中学2024届高三下学期5月模拟(三模)数学试题(B卷)



