名校
解题方法
1 . 如图,在四棱锥 中,平面
中,平面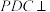 平面
平面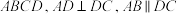 ,
,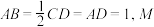 为棱
为棱 的中点.
的中点. 平面
平面 ;
;
(2)若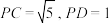 ,
,
(i)求二面角 的余弦值;
的余弦值;
(ii)在线段 上是否存在点Q,使得点Q到平面
上是否存在点Q,使得点Q到平面 的距离是
的距离是 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 中,平面
中,平面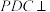 平面
平面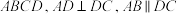 ,
,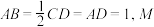 为棱
为棱 的中点.
的中点.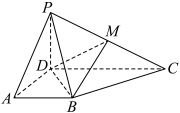
 平面
平面 ;
;(2)若
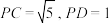 ,
,(i)求二面角
 的余弦值;
的余弦值;(ii)在线段
 上是否存在点Q,使得点Q到平面
上是否存在点Q,使得点Q到平面 的距离是
的距离是 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次
昨日更新
|
2428次组卷
|
20卷引用:上海市格致中学2023-2024学年高二下学期期中考试数学试题
上海市格致中学2023-2024学年高二下学期期中考试数学试题(已下线)专题03 空间向量及其应用全章复习攻略--高二期末考点大串讲(沪教版2020选修)(已下线)专题03空间向量及其应用--高二期末考点大串讲(沪教版2020选修)江苏省盐城市五校联考2023-2024学年高二下学期第一次学情调研检测(3月)数学试题湖南省常德市汉寿县第一中学2023-2024学年高二下学期3月月考数学试题福建省莆田第二十五中学2023-2024学年高二下学期期中考试数学试题(已下线)专题02 空间向量与立体几何--高二期末考点大串讲(苏教版2019选择性必修第二册)福建省三明第一中学2024-2025学年高二上学期8月月考数学试题(已下线)专题5 空间向量求值及范围问题【练】(高二期中压轴专项)福建省泉州市晋江市侨声中学2024-2025学年高二上学期教学质量监测(一)数学试卷福建省莆田第十中学2024-2025学年高二上学期10月月考数学试卷内蒙古自治区通辽市第一中学2024-2025学年高二上学期10月月考数学试题河北省石家庄精英未来高级中学2024-2025学年高二上学期第一次月考数学试题山东省新泰市紫光实验中学2024-2025学年高二上学期开学考试数学试题山东省济宁市嘉祥县第一中学2024-2025学年高二上学期第一次月考数学试题河北省邯郸市武安市第一中学2024-2025学年高二上学期10月期中考试数学试题(已下线)第06讲 空间向量的应用(二)-【暑假预科讲义】(人教A版2019选择性必修第一册)宁夏银川市第九中学2023-2024学年高一下学期期末考试数学试卷黑龙江省哈尔滨市第六中学校2023-2024学年高一下学期期末测试数学试题山东省泰安市肥城市慈明学校2023-2024学年高一下学期期末检测数学试卷
名校
2 . 如图,某苗圃有两个入口 、
、 ,
, ,欲在苗圃内开辟一块区域种植观赏植物.现有若干树苗放在苗圃外的
,欲在苗圃内开辟一块区域种植观赏植物.现有若干树苗放在苗圃外的 处,已知
处,已知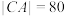 ,
,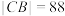 ,以AB所在直线为
,以AB所在直线为 轴,AB中点为原点建立直角坐标系.
轴,AB中点为原点建立直角坐标系.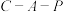 和
和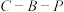 两条折线段路线搬运至
两条折线段路线搬运至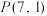 处,请判断哪条搬运路线最短?并说明理由;
处,请判断哪条搬运路线最短?并说明理由;
(2)工人准备将 处树苗运送到苗圃内的点
处树苗运送到苗圃内的点 处,计划合理设计点
处,计划合理设计点 的位置,使得沿
的位置,使得沿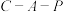 和
和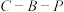 两条折线段路线运输的距离相等.请写出所有满足要求的点
两条折线段路线运输的距离相等.请写出所有满足要求的点 的轨迹方程.
的轨迹方程.
 、
、 ,
, ,欲在苗圃内开辟一块区域种植观赏植物.现有若干树苗放在苗圃外的
,欲在苗圃内开辟一块区域种植观赏植物.现有若干树苗放在苗圃外的 处,已知
处,已知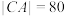 ,
,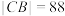 ,以AB所在直线为
,以AB所在直线为 轴,AB中点为原点建立直角坐标系.
轴,AB中点为原点建立直角坐标系.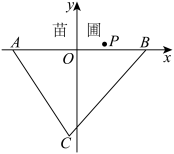
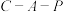 和
和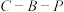 两条折线段路线搬运至
两条折线段路线搬运至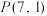 处,请判断哪条搬运路线最短?并说明理由;
处,请判断哪条搬运路线最短?并说明理由;(2)工人准备将
 处树苗运送到苗圃内的点
处树苗运送到苗圃内的点 处,计划合理设计点
处,计划合理设计点 的位置,使得沿
的位置,使得沿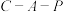 和
和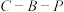 两条折线段路线运输的距离相等.请写出所有满足要求的点
两条折线段路线运输的距离相等.请写出所有满足要求的点 的轨迹方程.
的轨迹方程.
您最近一年使用:0次
名校
解题方法
3 . 如图,在棱长为2的正方体 中,
中, ,
, 分别是棱
分别是棱 ,
, 的中点,点
的中点,点 在
在 上,点
上,点 在
在 上,且
上,且 ,点
,点 在线段
在线段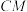 上运动,给出下列四个结论:
上运动,给出下列四个结论: 是
是 中点时,直线
中点时,直线 平面
平面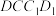 ;
;
②直线 到平面
到平面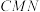 的距离是
的距离是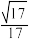 ;
;
③存在点 ,使得
,使得 ;
;
④ 面积的最小值是
面积的最小值是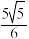 .
.
其中所有正确结论的个数是( )
 中,
中, ,
, 分别是棱
分别是棱 ,
, 的中点,点
的中点,点 在
在 上,点
上,点 在
在 上,且
上,且 ,点
,点 在线段
在线段 上运动,给出下列四个结论:
上运动,给出下列四个结论: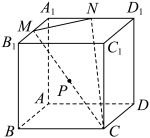
 是
是 中点时,直线
中点时,直线 平面
平面 ;
;②直线
 到平面
到平面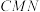 的距离是
的距离是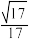 ;
;③存在点
 ,使得
,使得 ;
;④
 面积的最小值是
面积的最小值是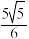 .
.其中所有正确结论的个数是( )
| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
昨日更新
|
364次组卷
|
3卷引用:上海市上海师范大学附属中学闵行分校2024-2025学年高二上学期期中联考数学试题
名校
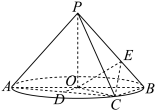
4 . 如图, 是圆
是圆 的直径,
的直径, 是圆
是圆 上异于
上异于 、
、 的动点,
的动点, 垂直于圆
垂直于圆 所在的平面,且
所在的平面,且 .
. 为线段
为线段 的中点,求证:
的中点,求证: 平面
平面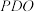 ;
;
(2)当三棱锥 体积的最大时,求异面直线
体积的最大时,求异面直线 与
与 所成角的大小;
所成角的大小;
(3)若 ,点
,点 在线段
在线段 上,求
上,求 的最小值.
的最小值.
 是圆
是圆 的直径,
的直径, 是圆
是圆 上异于
上异于 、
、 的动点,
的动点, 垂直于圆
垂直于圆 所在的平面,且
所在的平面,且 .
.
 为线段
为线段 的中点,求证:
的中点,求证: 平面
平面 ;
;(2)当三棱锥
 体积的最大时,求异面直线
体积的最大时,求异面直线 与
与 所成角的大小;
所成角的大小;(3)若
 ,点
,点 在线段
在线段 上,求
上,求 的最小值.
的最小值.
您最近一年使用:0次
解题方法
5 . 已知椭圆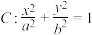 ,
,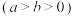 过点
过点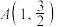 ,且长轴长是焦距的2倍.
,且长轴长是焦距的2倍.
(1)求椭圆 的标准方程;
的标准方程;
(2)若点 为椭圆
为椭圆 上的一个动点,求动点
上的一个动点,求动点 到定点
到定点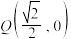 的最短距离;
的最短距离;
(3)若直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,且线段
,且线段 的垂直平分线过定点
的垂直平分线过定点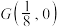 ,求
,求 的取值范围.
的取值范围.
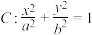 ,
,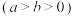 过点
过点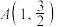 ,且长轴长是焦距的2倍.
,且长轴长是焦距的2倍.(1)求椭圆
 的标准方程;
的标准方程;(2)若点
 为椭圆
为椭圆 上的一个动点,求动点
上的一个动点,求动点 到定点
到定点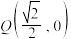 的最短距离;
的最短距离;(3)若直线
 与椭圆交于不同的两点
与椭圆交于不同的两点 ,且线段
,且线段 的垂直平分线过定点
的垂直平分线过定点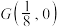 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
6 . 曲线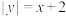 与曲线
与曲线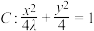 恰有两个不同交点,则实数
恰有两个不同交点,则实数 的取值范围为( )
的取值范围为( )
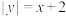 与曲线
与曲线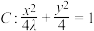 恰有两个不同交点,则实数
恰有两个不同交点,则实数 的取值范围为( )
的取值范围为( )A.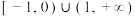 | B. |
C. | D.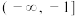 |
您最近一年使用:0次
名校
解题方法
7 . 如图,在长方体 中,
中,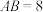 ,
,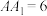 ,则棱
,则棱 与平面
与平面 的距离为
的距离为__________ .
 中,
中,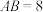 ,
,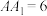 ,则棱
,则棱 与平面
与平面 的距离为
的距离为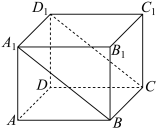
您最近一年使用:0次
8 . 如图,在四棱锥 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形,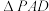 是正三角形,
是正三角形,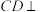 平面
平面 ,
, ,
, ,
, ,
, 分别是
分别是 ,
, ,
, ,
, 的中点.
的中点. 平面
平面 ;
;
(2)求平面 与平面
与平面 所成的锐二面角的大小;
所成的锐二面角的大小;
(3)在线段 上是否存在点
上是否存在点 ,使得直线
,使得直线 与平面
与平面 所成角为
所成角为 ,若存在,求线段
,若存在,求线段 的长度:若不存在,说明理由.
的长度:若不存在,说明理由.
 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形, 是正三角形,
是正三角形, 平面
平面 ,
, ,
, ,
, ,
, 分别是
分别是 ,
, ,
, ,
, 的中点.
的中点.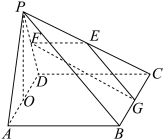
 平面
平面 ;
;(2)求平面
 与平面
与平面 所成的锐二面角的大小;
所成的锐二面角的大小;(3)在线段
 上是否存在点
上是否存在点 ,使得直线
,使得直线 与平面
与平面 所成角为
所成角为 ,若存在,求线段
,若存在,求线段 的长度:若不存在,说明理由.
的长度:若不存在,说明理由.
您最近一年使用:0次
解题方法
9 . 在 中,
中, ,
,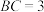 ,
, ,
, 、
、 分别是
分别是 、
、 上的点,满足
上的点,满足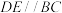 且
且 ,将
,将 沿
沿 折起到
折起到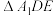 的位置,使
的位置,使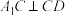 ,
, 是
是 的中点,如图所示.
的中点,如图所示.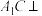 平面
平面 ;
;
(2)求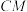 与平面
与平面 所成角的大小;
所成角的大小;
(3)在线段 上是否存在点
上是否存在点 (
( 不与端点
不与端点 、
、 重合),使
重合),使 ?若存在,求出
?若存在,求出 与
与 的比值;若不存在,请说明理由.
的比值;若不存在,请说明理由.
 中,
中, ,
,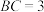 ,
, ,
, 、
、 分别是
分别是 、
、 上的点,满足
上的点,满足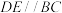 且
且 ,将
,将 沿
沿 折起到
折起到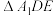 的位置,使
的位置,使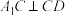 ,
, 是
是 的中点,如图所示.
的中点,如图所示.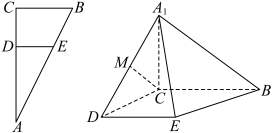
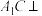 平面
平面 ;
;(2)求
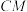 与平面
与平面 所成角的大小;
所成角的大小;(3)在线段
 上是否存在点
上是否存在点 (
( 不与端点
不与端点 、
、 重合),使
重合),使 ?若存在,求出
?若存在,求出 与
与 的比值;若不存在,请说明理由.
的比值;若不存在,请说明理由.
您最近一年使用:0次
解题方法
10 . 如图,在四棱锥 中,底面
中,底面 为正方形,
为正方形, 平面
平面 ,
, 为
为 中点.
中点. 平面
平面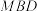 ;
;
(2)若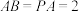 ,求点
,求点 到平面
到平面 的距离.
的距离.
 中,底面
中,底面 为正方形,
为正方形, 平面
平面 ,
, 为
为 中点.
中点.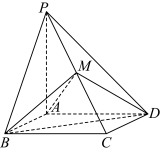
 平面
平面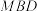 ;
;(2)若
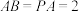 ,求点
,求点 到平面
到平面 的距离.
的距离.
您最近一年使用:0次



