1 . 若 是一个集合,
是一个集合, 是一个以
是一个以 的某些子集为元素的集合,且满足:①
的某些子集为元素的集合,且满足:① 属于
属于 ,空集
,空集 属于
属于 ;②
;② 中任意多个元素的并集属于
中任意多个元素的并集属于 ;③
;③ 中任意多个元素的交集属于
中任意多个元素的交集属于 ,则称
,则称 是集合
是集合 上的一个拓扑.已知函数
上的一个拓扑.已知函数 ,其中[x]表示不大于
,其中[x]表示不大于 的最大整数,当
的最大整数,当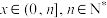 时,函数
时,函数 值域为集合
值域为集合 ,则集合
,则集合 上的含有4个元素的拓扑
上的含有4个元素的拓扑 的个数为
的个数为______ .
 是一个集合,
是一个集合, 是一个以
是一个以 的某些子集为元素的集合,且满足:①
的某些子集为元素的集合,且满足:① 属于
属于 ,空集
,空集 属于
属于 ;②
;② 中任意多个元素的并集属于
中任意多个元素的并集属于 ;③
;③ 中任意多个元素的交集属于
中任意多个元素的交集属于 ,则称
,则称 是集合
是集合 上的一个拓扑.已知函数
上的一个拓扑.已知函数 ,其中[x]表示不大于
,其中[x]表示不大于 的最大整数,当
的最大整数,当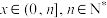 时,函数
时,函数 值域为集合
值域为集合 ,则集合
,则集合 上的含有4个元素的拓扑
上的含有4个元素的拓扑 的个数为
的个数为
您最近一年使用:0次
2024-04-29更新
|
484次组卷
|
3卷引用:第一章 排列组合与二项式定理 专题三 组合 微点2 组合综合训练【培优版】
(已下线)第一章 排列组合与二项式定理 专题三 组合 微点2 组合综合训练【培优版】浙江省温州新力量联盟2023-2024学年高二下学期4月期中考试数学试题江苏省前黄高级中学2024届高三下学期三模适应性考试数学试题
名校
2 . 已知 为正整数,对于给定的函数
为正整数,对于给定的函数 ,定义一个
,定义一个 次多项式
次多项式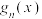 如下:
如下: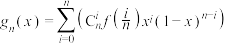
(1)当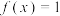 时,求
时,求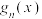 ;
;
(2)当 时,求
时,求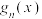 ;
;
(3)当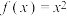 时,求
时,求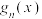 .
.
 为正整数,对于给定的函数
为正整数,对于给定的函数 ,定义一个
,定义一个 次多项式
次多项式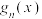 如下:
如下: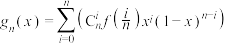
(1)当
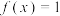 时,求
时,求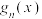 ;
;(2)当
 时,求
时,求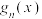 ;
;(3)当
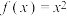 时,求
时,求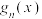 .
.
您最近一年使用:0次
2023·江西·二模
解题方法
3 . 李华在研究化学反应时,把反应抽象为小球之间的碰撞,而碰撞又分为有效碰撞和无效碰撞,李华有3个小球 和3个小球
和3个小球 ,当发生有效碰撞时,
,当发生有效碰撞时, ,
, 上的计数器分别增加2计数和1计数,
上的计数器分别增加2计数和1计数, ,
, 球两两发生有效碰撞的概率均为
球两两发生有效碰撞的概率均为 ,现在李华取三个球让他们之间两两碰撞,结束后从中随机取一个球,发现其上计数为2,则李华一开始取出的三个球里,小球
,现在李华取三个球让他们之间两两碰撞,结束后从中随机取一个球,发现其上计数为2,则李华一开始取出的三个球里,小球 个数的期望是( )个
个数的期望是( )个
 和3个小球
和3个小球 ,当发生有效碰撞时,
,当发生有效碰撞时, ,
, 上的计数器分别增加2计数和1计数,
上的计数器分别增加2计数和1计数, ,
, 球两两发生有效碰撞的概率均为
球两两发生有效碰撞的概率均为 ,现在李华取三个球让他们之间两两碰撞,结束后从中随机取一个球,发现其上计数为2,则李华一开始取出的三个球里,小球
,现在李华取三个球让他们之间两两碰撞,结束后从中随机取一个球,发现其上计数为2,则李华一开始取出的三个球里,小球 个数的期望是( )个
个数的期望是( )个| A.1.2 | B.1.6 | C.1.8 | D.2 |
您最近一年使用:0次
2023-04-10更新
|
1849次组卷
|
6卷引用:模块八 专题5 以概率与统计为背景的压轴小题
(已下线)模块八 专题5 以概率与统计为背景的压轴小题(已下线)第六节 离散型随机变量的数字特征 B卷素养养成卷 一轮复习点点通(已下线)【练】专题三 复杂背景的概率计算问题(压轴大全)(已下线)第三章 随机变量及其分布列 专题一 随机变量的期望 微点3 随机变量的分布列、期望综合训练【培优版】(已下线)江西省名校协作体联盟2023届高三第二次联考模拟考试数学(理)试题(已下线)专题7.10 随机变量及其分布全章综合测试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
名校
解题方法
4 . 小林同学喜欢吃4种坚果:核桃、腰果、杏仁、榛子,他有5种颜色的“每日坚果”袋.每个袋子中至少装1种坚果,至多装4种坚果.小林同学希望五个袋子中所装坚果种类各不相同,且每一种坚果在袋子中出现的总次数均为偶数,那么不同的方案数为( )
| A.20160 | B.20220 | C.20280 | D.20340 |
您最近一年使用:0次
2022-04-07更新
|
4552次组卷
|
12卷引用:2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(6月1日)
(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(6月1日)(已下线)2022年高考考前20天终极冲刺攻略(四)【理科数学】 (6月1日)(已下线)专题12 计数原理(理)(已下线)专题10-1 排列组合20种模型方法归类-3(已下线)专题18 排列组合与二项式定理(已下线)计数原理与排列组合(已下线)第一章 排列组合与二项式定理 专题四 排列与组合综合 微点5 排列与组合综合(五)【培优版】湖北省二十一所重点中学2022届高三下学期第三次联考数学试题(已下线)高二数学下学期期末精选50题(压轴版)-2021-2022学年高二数学考试满分全攻略(人教A版2019选修第二册+第三册)湖北省九校教研协作体2023届高三上学期起点考试数学试题安徽省定远中学2023届高三下学期6月高考预测数学试卷(已下线)6.2.3组合-6.2.4组合数——课时作业(提升版)
5 . “迎冬奥,跨新年,向未来”,水球中学将开展自由式滑雪接力赛.自由式滑雪接力赛设有空中技巧、雪上技巧和雪上芭蕾三个项目,参赛选手每人展示其中一个项目.现安排两名男生和两名女生组队参赛,若要求相邻出场选手展示不同项目,女生中至少一人展示雪上芭蕾项目,且三个项目均有所展示,则共有___ 种出场顺序与项目展示方案.(用数字作答)
您最近一年使用:0次
2022-02-15更新
|
1782次组卷
|
5卷引用:专题10-1 排列组合20种模型方法归类-3
(已下线)专题10-1 排列组合20种模型方法归类-3(已下线)第一章 排列组合与二项式定理 专题二 排列 微点2 排列综合训练【培优版】浙江省2022届高三水球高考命题研究组方向性测试Ⅴ数学试题重庆市万州第二高级中学2021-2022学年高二下学期6月第四次质量检测数学试题(已下线)6.2.1排列-6.2.2排列数——课时作业(提升版)
6 . 某校高二年级共有10个班级,5位教学教师,每位教师教两个班级,其中姜老师一定教1班,张老师一定教3班,王老师一定教8班,秋老师至少教9班和10班中的一个班,曲老师不教2班和6班,王老师不教5班,则不同的排课方法种数______ .
您最近一年使用:0次
2021-03-22更新
|
3492次组卷
|
8卷引用:专题10-1 排列组合20种模型方法归类-4
(已下线)专题10-1 排列组合20种模型方法归类-4(已下线)专题06计数原理--高二期末考点大串讲(沪教版2020选修)黑龙江省哈尔滨市第三中学2020-2021学年度上学期高二学年第二模块考试(理科)数学试题(已下线)第6章 计数原理(新文化与压轴30题专练)2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)(已下线)上海市华东师范大学第二附属中学2022-2023学年高二下学期期末数学试题(已下线)6.2.1排列-6.2.2排列数——课时作业(提升版)(已下线)6.2.1排列-6.2.2排列数——课时作业(巩固版)广东省深圳实验学校高中部2024届高三教学情况测试(一)数学试题
19-20高二·全国·单元测试
解题方法
7 . 冠状病毒是一个大型病毒家族,已知可引起感冒以及中东呼吸综合征( )和严重急性呼吸综合征(
)和严重急性呼吸综合征(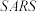 )等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(
)等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(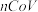 )是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有n(
)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有n( )份血液样本,有以下两种检验方式:方式一:逐份检验,则需要检验n次.方式二:混合检验,将其中k(
)份血液样本,有以下两种检验方式:方式一:逐份检验,则需要检验n次.方式二:混合检验,将其中k( 且
且 )份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为
)份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为 .假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(
.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p( ).现取其中k(
).现取其中k( 且
且 )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为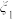 ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为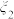 .
.
(1)若 ,试求p关于k的函数关系式
,试求p关于k的函数关系式 ;
;
(2)若p与干扰素计量 相关,其中
相关,其中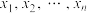 (
( )是不同的正实数,满足
)是不同的正实数,满足 且
且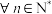 (
( )都有
)都有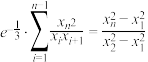 成立.
成立.
(i)求证:数列 等比数列;
等比数列;
(ii)当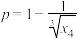 时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值
时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值
 )和严重急性呼吸综合征(
)和严重急性呼吸综合征(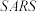 )等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(
)等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(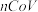 )是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有n(
)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有n( )份血液样本,有以下两种检验方式:方式一:逐份检验,则需要检验n次.方式二:混合检验,将其中k(
)份血液样本,有以下两种检验方式:方式一:逐份检验,则需要检验n次.方式二:混合检验,将其中k( 且
且 )份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为
)份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为 .假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(
.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p( ).现取其中k(
).现取其中k( 且
且 )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为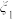 ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为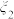 .
.(1)若
 ,试求p关于k的函数关系式
,试求p关于k的函数关系式 ;
;(2)若p与干扰素计量
 相关,其中
相关,其中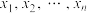 (
( )是不同的正实数,满足
)是不同的正实数,满足 且
且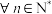 (
( )都有
)都有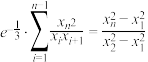 成立.
成立.(i)求证:数列
 等比数列;
等比数列;(ii)当
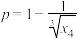 时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值
时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值
您最近一年使用:0次
2020-08-28更新
|
2227次组卷
|
7卷引用:专题7.1 概率中的应用问题 -玩转压轴题,进军满分之2021高考数学选择题填空题
(已下线)专题7.1 概率中的应用问题 -玩转压轴题,进军满分之2021高考数学选择题填空题(已下线)第51讲 概率与统计综合问题-2022年新高考数学二轮专题突破精练(已下线)专题9-1 概率与统计及分布列归类(理)(讲+练)-2(已下线)专题8-2分布列综合归类-2(已下线)第三章统计案例单元测试(基础版) -突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)第二章随机变量及其分步单元测试(巅峰版) -突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)(已下线)综合测试卷(巅峰版) -突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)
名校
解题方法
8 . 在孟德尔遗传理论中,称遗传性状依赖的特定携带者为遗传因子,遗传因子总是成对出现,例如,豌豆携带这样一对遗传因子: 使之开红花,
使之开红花, 使之开白花,两个因子的相互组合可以构成三种不同的遗传性状:
使之开白花,两个因子的相互组合可以构成三种不同的遗传性状: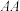 为开红花,
为开红花,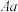 和
和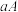 一样不加区分为开粉色花,
一样不加区分为开粉色花,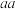 为开白色花,生物在繁衍后代的过程中,后代的每一对遗传因子都包含一个父本的遗传因子和一个母本的遗传因子,而因为生殖细胞是由分裂过程产生的,每一个上一代的遗传因子以
为开白色花,生物在繁衍后代的过程中,后代的每一对遗传因子都包含一个父本的遗传因子和一个母本的遗传因子,而因为生殖细胞是由分裂过程产生的,每一个上一代的遗传因子以 的概率传给下一代,而且各代的遗传过程都是相互独立的,可以把第
的概率传给下一代,而且各代的遗传过程都是相互独立的,可以把第 代的遗传设想为第
代的遗传设想为第 次试验的结果,每一次试验就如同抛一枚均匀的硬币,比如对具有性状
次试验的结果,每一次试验就如同抛一枚均匀的硬币,比如对具有性状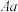 的父本来说,如果抛出正面就选择因子
的父本来说,如果抛出正面就选择因子 ,如果抛出反面就选择因子
,如果抛出反面就选择因子 ,概率都是
,概率都是 ,对母本也一样,父本、母本各自随机选择得到的遗传因子再配对形成子代的遗传性状,假设三种遗传性状
,对母本也一样,父本、母本各自随机选择得到的遗传因子再配对形成子代的遗传性状,假设三种遗传性状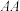 ,
,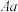 (或
(或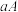 ),
),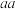 在父本和母本中以同样的比例
在父本和母本中以同样的比例 出现,则在随机杂交试验中,遗传因子
出现,则在随机杂交试验中,遗传因子 被选中的概率是
被选中的概率是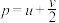 ,遗传因子
,遗传因子 被选中的概率是
被选中的概率是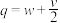 ,称
,称 、
、 分别为父本和母本中遗传因子
分别为父本和母本中遗传因子 和
和 的频率,
的频率,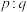 实际上是父本和母本中两个遗传因子的个数之比,基于以上常识回答以下问题:
实际上是父本和母本中两个遗传因子的个数之比,基于以上常识回答以下问题:
(1)如果植物的上代父本、母本的遗传性状都是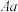 ,后代遗传性状为
,后代遗传性状为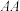 ,
,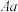 (或
(或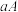 ),
),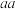 的概率分别是多少?
的概率分别是多少?
(2)对某一植物,经过实验观察发现遗传性状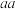 具有重大缺陷,可人工剔除,从而使得父本和母本中仅有遗传性状为
具有重大缺陷,可人工剔除,从而使得父本和母本中仅有遗传性状为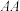 ,
,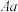 (或
(或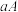 )的个体,在进行第一代杂交实验时,假设遗传因子
)的个体,在进行第一代杂交实验时,假设遗传因子 被选中的概率为
被选中的概率为 ,
, 被选中的概率为
被选中的概率为 ,其中
,其中 、
、 为定值且
为定值且 ,求杂交所得子代的三种遗传性状
,求杂交所得子代的三种遗传性状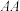 ,
,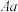 (或
(或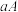 ),
),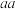 所占的比例
所占的比例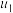 ,
,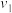 ,
, ;
;
(3)继续对(2)中的植物进行杂交实验,每次杂交前都需要剔除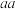 的个体.假设得到的第
的个体.假设得到的第 代总体中3种遗传性状
代总体中3种遗传性状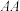 ,
,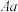 (或
(或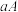 ),
),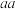 所占的比例分别为:
所占的比例分别为: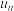 ,
, ,
,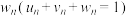 ,设第
,设第 代遗传因子
代遗传因子 和
和 的频率分别为
的频率分别为 和
和 ,已知有以下公式
,已知有以下公式 ,
, ,
,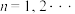
(ⅰ)证明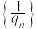 是等差数列;
是等差数列;
(ⅱ)求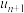 ,
, ,
,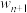 的通项公式,如果这种剔除某种遗传性状的随机杂交实验长期进行下去,会有什么现象发生?
的通项公式,如果这种剔除某种遗传性状的随机杂交实验长期进行下去,会有什么现象发生?
 使之开红花,
使之开红花, 使之开白花,两个因子的相互组合可以构成三种不同的遗传性状:
使之开白花,两个因子的相互组合可以构成三种不同的遗传性状: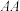 为开红花,
为开红花,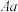 和
和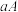 一样不加区分为开粉色花,
一样不加区分为开粉色花,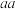 为开白色花,生物在繁衍后代的过程中,后代的每一对遗传因子都包含一个父本的遗传因子和一个母本的遗传因子,而因为生殖细胞是由分裂过程产生的,每一个上一代的遗传因子以
为开白色花,生物在繁衍后代的过程中,后代的每一对遗传因子都包含一个父本的遗传因子和一个母本的遗传因子,而因为生殖细胞是由分裂过程产生的,每一个上一代的遗传因子以 的概率传给下一代,而且各代的遗传过程都是相互独立的,可以把第
的概率传给下一代,而且各代的遗传过程都是相互独立的,可以把第 代的遗传设想为第
代的遗传设想为第 次试验的结果,每一次试验就如同抛一枚均匀的硬币,比如对具有性状
次试验的结果,每一次试验就如同抛一枚均匀的硬币,比如对具有性状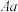 的父本来说,如果抛出正面就选择因子
的父本来说,如果抛出正面就选择因子 ,如果抛出反面就选择因子
,如果抛出反面就选择因子 ,概率都是
,概率都是 ,对母本也一样,父本、母本各自随机选择得到的遗传因子再配对形成子代的遗传性状,假设三种遗传性状
,对母本也一样,父本、母本各自随机选择得到的遗传因子再配对形成子代的遗传性状,假设三种遗传性状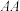 ,
,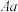 (或
(或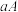 ),
),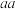 在父本和母本中以同样的比例
在父本和母本中以同样的比例 出现,则在随机杂交试验中,遗传因子
出现,则在随机杂交试验中,遗传因子 被选中的概率是
被选中的概率是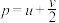 ,遗传因子
,遗传因子 被选中的概率是
被选中的概率是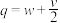 ,称
,称 、
、 分别为父本和母本中遗传因子
分别为父本和母本中遗传因子 和
和 的频率,
的频率,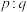 实际上是父本和母本中两个遗传因子的个数之比,基于以上常识回答以下问题:
实际上是父本和母本中两个遗传因子的个数之比,基于以上常识回答以下问题:(1)如果植物的上代父本、母本的遗传性状都是
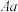 ,后代遗传性状为
,后代遗传性状为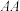 ,
,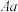 (或
(或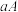 ),
),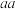 的概率分别是多少?
的概率分别是多少?(2)对某一植物,经过实验观察发现遗传性状
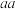 具有重大缺陷,可人工剔除,从而使得父本和母本中仅有遗传性状为
具有重大缺陷,可人工剔除,从而使得父本和母本中仅有遗传性状为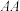 ,
,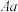 (或
(或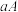 )的个体,在进行第一代杂交实验时,假设遗传因子
)的个体,在进行第一代杂交实验时,假设遗传因子 被选中的概率为
被选中的概率为 ,
, 被选中的概率为
被选中的概率为 ,其中
,其中 、
、 为定值且
为定值且 ,求杂交所得子代的三种遗传性状
,求杂交所得子代的三种遗传性状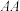 ,
,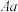 (或
(或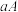 ),
),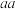 所占的比例
所占的比例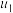 ,
,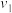 ,
, ;
;(3)继续对(2)中的植物进行杂交实验,每次杂交前都需要剔除
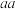 的个体.假设得到的第
的个体.假设得到的第 代总体中3种遗传性状
代总体中3种遗传性状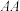 ,
,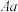 (或
(或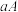 ),
),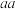 所占的比例分别为:
所占的比例分别为: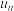 ,
, ,
,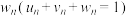 ,设第
,设第 代遗传因子
代遗传因子 和
和 的频率分别为
的频率分别为 和
和 ,已知有以下公式
,已知有以下公式 ,
, ,
,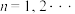
(ⅰ)证明
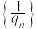 是等差数列;
是等差数列;(ⅱ)求
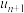 ,
, ,
,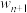 的通项公式,如果这种剔除某种遗传性状的随机杂交实验长期进行下去,会有什么现象发生?
的通项公式,如果这种剔除某种遗传性状的随机杂交实验长期进行下去,会有什么现象发生?
您最近一年使用:0次
2020-08-09更新
|
3253次组卷
|
8卷引用:专题10-2 概率压轴大题(理)-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)
(已下线)专题10-2 概率压轴大题(理)-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)(已下线)第04讲 条件概率与全概率(核心考点讲与练)-2021-2022学年高二数学考试满分全攻略(人教A版2019选修第二册+第三册)(已下线)专题9-1 概率与统计及分布列归类(理)(讲+练)-2(已下线)专题8-2分布列综合归类-2(已下线)专题1 概率压轴大题【讲】(已下线)第二章 概率 专题四 条件概率、全概率公式和贝叶斯公式 微点3 条件概率、全概率公式和贝叶斯公式综合训练【培优版】(已下线)第五章 概率统计创新问题 专题二 概率统计与数列交汇 微点1 概率统计与数列交汇(一)【培优版】湖北省襄阳市第四中学2020届高三下学期第四次模拟考试数学(理)试题
9 . 口袋中有大小、形状、质地相同的两个白球和三个黑球.现有一抽奖游戏规则如下:抽奖者每次有放回的从口袋中随机取出一个球,最多取球2n+1(n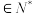 )次.若取出白球的累计次数达到n+1时,则终止取球且获奖,其它情况均不获奖.记获奖概率为
)次.若取出白球的累计次数达到n+1时,则终止取球且获奖,其它情况均不获奖.记获奖概率为 .
.
(1)求 ;
;
(2)证明: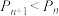 .
.
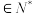 )次.若取出白球的累计次数达到n+1时,则终止取球且获奖,其它情况均不获奖.记获奖概率为
)次.若取出白球的累计次数达到n+1时,则终止取球且获奖,其它情况均不获奖.记获奖概率为 .
.(1)求
 ;
;(2)证明:
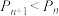 .
.
您最近一年使用:0次
2020-06-05更新
|
1961次组卷
|
5卷引用:专题10-2 概率压轴大题(理)-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)
(已下线)专题10-2 概率压轴大题(理)-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)(已下线)第五章 概率统计创新问题 专题二 概率统计与数列交汇 微点2 概率统计与数列交汇(二)【培优版】江苏省南京市2020届高三下学期6月第三次模拟考试数学试题湖北省九校教研协作体2022-2023学年高二上学期9月联考数学试题(已下线)4.1.3独立性与条件概率的关系(2)
10 . (1)求证: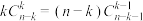 ;
;
(2)求证: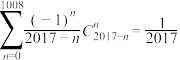 .
.
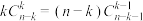 ;
;(2)求证:
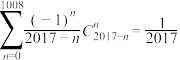 .
.
您最近一年使用:0次



