名校
1 . 已知抛物线 :
: ,圆
,圆 :
: ,在抛物线
,在抛物线 上任取一点
上任取一点 ,向圆
,向圆 作两条切线
作两条切线 和
和 ,切点分别为
,切点分别为 ,
, ,则
,则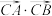 的取值范围是
的取值范围是______ .
 :
: ,圆
,圆 :
: ,在抛物线
,在抛物线 上任取一点
上任取一点 ,向圆
,向圆 作两条切线
作两条切线 和
和 ,切点分别为
,切点分别为 ,
, ,则
,则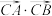 的取值范围是
的取值范围是
您最近一年使用:0次
2022-11-25更新
|
2514次组卷
|
9卷引用:辽宁省沈阳市第二中学2022-2023学年高三上学期12月月考数学试题
辽宁省沈阳市第二中学2022-2023学年高三上学期12月月考数学试题江苏省南通市通州区2022-2023学年高三上学期期中复习数学试题2023年江苏省苏州市高考模拟数学试题(二)(已下线)专题12 圆锥曲线压轴小题常见题型全归纳(精讲精练)-3江西省上饶一中、上饶中学2023届高三高考仿真模拟数学(文)试题(已下线)第8课时 课中 抛物线的几何性质(已下线)第03讲 3.3抛物线(8大题型训练)-【练透核心考点】2023-2024学年高二数学上学期重点题型方法与技巧(人教A版2019选择性必修第一册)重庆市江北区字水中学2023-2024学年高二上学期第二次月考数学试题(已下线)3.3.2 抛物线的简单几何性质(分层练习)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第一册)
名校
2 . 如图所示,在△ABC中,点D是边BC的中点,点E是线段上靠近A的一个三等分点,过点E的直线与边AB,AC分别交于点P,Q.设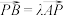 ,
, ,其中
,其中 ,
,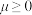
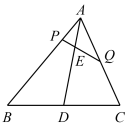
(1)求证: 为定值,并求此定值;
为定值,并求此定值;
(2)设△APQ的面积为 ,△ABC的面积为
,△ABC的面积为 ,求
,求 的最小值.
的最小值.
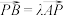 ,
, ,其中
,其中 ,
,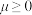

(1)求证:
 为定值,并求此定值;
为定值,并求此定值;(2)设△APQ的面积为
 ,△ABC的面积为
,△ABC的面积为 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2022-10-29更新
|
673次组卷
|
2卷引用:辽宁省沈阳市东北育才学校2022-2023学年高三上学期联合考试数学试题
名校
3 . 已知 是定义在R的偶函数,且
是定义在R的偶函数,且 ,
, .
.
(1)求 的解析式;
的解析式;
(2)设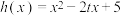 ,若存在
,若存在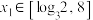 ,对任意的
,对任意的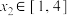 ,都有
,都有 ,求实数t的取值范围.
,求实数t的取值范围.
 是定义在R的偶函数,且
是定义在R的偶函数,且 ,
, .
.(1)求
 的解析式;
的解析式;(2)设
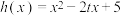 ,若存在
,若存在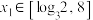 ,对任意的
,对任意的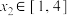 ,都有
,都有 ,求实数t的取值范围.
,求实数t的取值范围.
您最近一年使用:0次
2022-10-29更新
|
2399次组卷
|
7卷引用:辽宁省沈阳市东北育才学校2022-2023学年高三上学期联合考试数学试题
名校
解题方法
4 . 下列函数中,最小值为4的是( )
A. | B.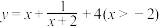 |
C. | D. |
您最近一年使用:0次
2022-09-06更新
|
1847次组卷
|
5卷引用:辽宁省沈阳市第三十一中学2022-2023学年高三上学期开学考试数学试题
辽宁省沈阳市第三十一中学2022-2023学年高三上学期开学考试数学试题重庆市长寿中学校2023届高三上学期期中数学试题海南省海口嘉勋高级中学2023届高三上学期10月检测数学试题(已下线)考点巩固卷02 一元二次不等式及基本不等式(十二大考点)(已下线)第一章 集合、常用逻辑用语与不等式 专题3 不等式中的最值(范围)问题
名校
5 . 已知定义域为 的函数
的函数 满足
满足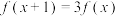 ,且当
,且当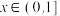 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( )
 的函数
的函数 满足
满足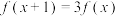 ,且当
,且当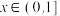 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( )A.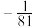 | B.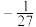 | C.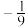 | D. |
您最近一年使用:0次
2022-04-15更新
|
1404次组卷
|
3卷引用:辽宁省沈阳市第一二〇中学2021-2022学年高三下学期4月月考数学试题
名校
解题方法
6 . 一般地,若函数 的定义域为
的定义域为 ,值域为
,值域为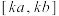 ,则称
,则称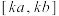 为
为 的“
的“ 倍跟随区间”;若函数
倍跟随区间”;若函数 的定义域为
的定义域为 ,值域也为
,值域也为 ,则称
,则称 为
为 的“跟随区间”.下列结论正确的是( )
的“跟随区间”.下列结论正确的是( )
 的定义域为
的定义域为 ,值域为
,值域为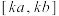 ,则称
,则称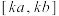 为
为 的“
的“ 倍跟随区间”;若函数
倍跟随区间”;若函数 的定义域为
的定义域为 ,值域也为
,值域也为 ,则称
,则称 为
为 的“跟随区间”.下列结论正确的是( )
的“跟随区间”.下列结论正确的是( )A.若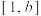 为 为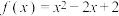 的跟随区间,则 的跟随区间,则 |
B.函数 存在跟随区间 存在跟随区间 |
C.若函数 存在跟随区间,则 存在跟随区间,则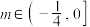 |
D.二次函数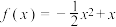 存在“3倍跟随区间” 存在“3倍跟随区间” |
您最近一年使用:0次
2022-12-08更新
|
1104次组卷
|
30卷引用:辽宁省沈阳市东北育才学校2022届高三上学期联合考试(二模)数学试题
辽宁省沈阳市东北育才学校2022届高三上学期联合考试(二模)数学试题(已下线)专题3.2—函数的值域-2022届高三数学一轮复习精讲精练(已下线)专题06函数的单调性及最值-2022年(新高考)数学高频考点+重点题型(已下线)专题2.3 函数的定义域与值域-重难点题型精讲-2022年高考数学一轮复习举一反三系列(新高考地区专用)(已下线)查补易混易错点01 函数与导数-【查漏补缺】2022年高考数学三轮冲刺过关(新高考专用)江苏省徐州市第七中学2022届高三下学期高考前模拟一数学试题(已下线)重难点01七种零点问题-3重庆市西南大学附属中学2021届高三上学期第一次月考数学试题(已下线)黄金卷09-【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(山东高考专用)(已下线)专题22 数学文化(客观题)-2021年高考数学二轮复习热点题型精选精练(新高考地区专用)江苏省无锡市天一中学2021届高三下学期第三次调研模拟考试数学试题重庆市育才中学2022届高三上学期高考适应性考试一数学试题河北省正定中学2021届高三上学期第四次月考数学试题湖南省长沙市宁乡市2021-2022学年高三上学期11月调研考试数学试题湖北省武汉市2022-2023学年高一上学期期中模拟数学试题广东省惠州市第一中学2022-2023学年高一上学期期中数学试题湖北省武汉市水果湖高级中学2022-2023学年高一上学期10月线上月考数学试题福建省福州市连江第一中学2022-2023学年高一上学期11月期中考试数学试题浙江省之江中学2022-2023学年高一上学期期中数学试题北师大版2019必修第一册综合检测卷-2022-2023学年高一数学北师大版2019必修第一册四川省射洪中学校2022-2023学年高一上学期期中数学试题湖北省武汉市黄陂一中盘龙校区2022-2023学年高一上学期11月适应性考试数学试题福建省永泰县第一中学2022-2023学年高一上学期适应性考试数学试题(已下线)模块四 题型突破篇 小题进阶提升练(3)(已下线)专题06 函数的单调性及最值重庆市南开中学2020-2021学年高一上学期11月月考数学试题江西省赣州市赣县第三中学2021-2022学年高一上学期期中适应考试数学试题浙江省北斗联盟2021-2022学年高一上学期期中联考数学试题重庆市暨华中学校2021-2022学年高一上学期期中数学试题(已下线)模块四 专题2 题型突破篇 小题进阶提升练(1)
名校
解题方法
7 . 已知 ,
, ,
,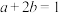 ,则( )
,则( )
 ,
, ,
,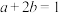 ,则( )
,则( )A. 的最小值为25 的最小值为25 |
B.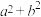 的最小值为 的最小值为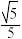 |
C. 的最小值为 的最小值为 |
D.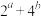 的最小值为 的最小值为 |
您最近一年使用:0次
2021-08-24更新
|
737次组卷
|
5卷引用:辽宁省锦州市黑山县2023届高三上学期10月月考数学试题
辽宁省锦州市黑山县2023届高三上学期10月月考数学试题(已下线)考点01 不等式-2022年高考数学(文)一轮复习小题多维练(全国通用)山东省泰安英雄山中学2022-2023学年高三上学期第一次月考数学试题山东省枣庄市第八中学2021-2022学年高三上学期9月月考数学试题江苏省南京市鼓楼区2020-2021学年高二下学期期末数学试题
名校
解题方法
8 . 如图,空间直角坐标系中,四棱锥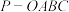 的底面是边长为
的底面是边长为 的正方形,且底面在
的正方形,且底面在 平面内,点
平面内,点 在
在 轴正半轴上,
轴正半轴上, 平面
平面 ,侧棱
,侧棱 与底面所成角为
与底面所成角为 .
.
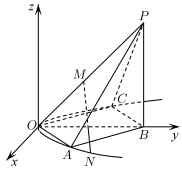
(1)若 是顶点在原点,且过
是顶点在原点,且过 、
、 两点的抛物线上的动点,试给出
两点的抛物线上的动点,试给出 与
与 满足的关系式;
满足的关系式;
(2)若 是棱
是棱 上的一个定点,它到平面
上的一个定点,它到平面 的距离为
的距离为 (
(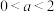 ),写出
),写出 、
、 两点之间的距离
两点之间的距离 ,并求
,并求 的最小值;
的最小值;
(3)是否存在一个实数 (
(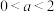 ),使得当
),使得当 取得最小值时,异面直线
取得最小值时,异面直线 与
与 互相垂直?请说明理由;
互相垂直?请说明理由;
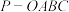 的底面是边长为
的底面是边长为 的正方形,且底面在
的正方形,且底面在 平面内,点
平面内,点 在
在 轴正半轴上,
轴正半轴上, 平面
平面 ,侧棱
,侧棱 与底面所成角为
与底面所成角为 .
.
(1)若
 是顶点在原点,且过
是顶点在原点,且过 、
、 两点的抛物线上的动点,试给出
两点的抛物线上的动点,试给出 与
与 满足的关系式;
满足的关系式;(2)若
 是棱
是棱 上的一个定点,它到平面
上的一个定点,它到平面 的距离为
的距离为 (
(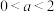 ),写出
),写出 、
、 两点之间的距离
两点之间的距离 ,并求
,并求 的最小值;
的最小值;(3)是否存在一个实数
 (
(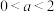 ),使得当
),使得当 取得最小值时,异面直线
取得最小值时,异面直线 与
与 互相垂直?请说明理由;
互相垂直?请说明理由;
您最近一年使用:0次
2022-06-23更新
|
707次组卷
|
5卷引用:辽宁省部分高中2021-2022学年高三上学期期中评测数学试题
辽宁省部分高中2021-2022学年高三上学期期中评测数学试题(已下线)专题32 空间向量及其应用-62018年上海市复旦附中高三5月三模数学试题上海市复旦大学附属中学2016届高三下学期5月月考数学试题(已下线)专题19 空间几何解答题(理科)-2



