名校
解题方法
1 . 在 中,
中, 为边
为边 上任意一点,
上任意一点, 为
为 的中点,且满足
的中点,且满足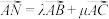 ,则
,则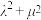 的最小值为
的最小值为________ .
 中,
中, 为边
为边 上任意一点,
上任意一点, 为
为 的中点,且满足
的中点,且满足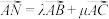 ,则
,则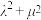 的最小值为
的最小值为
您最近一年使用:0次
2022-11-17更新
|
1128次组卷
|
5卷引用:江西省丰城中学2023届高三上学期第四次段考数学(文)试题
江西省丰城中学2023届高三上学期第四次段考数学(文)试题山东省德州市2022-2023学年高三上学期期中数学试题(已下线)重难专攻(六) 平面向量的最值问题 讲(已下线)重难点突破03 最全归纳平面向量中的范围与最值问题 (十大题型)-1(已下线)第04讲 平面向量的数乘运算
名校
2 . 已知函数 .
.
(1)讨论 的单调性;
的单调性;
(2) 时,设
时,设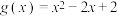 ,若对任意
,若对任意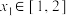 ,均存在
,均存在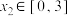 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
 .
.(1)讨论
 的单调性;
的单调性;(2)
 时,设
时,设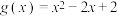 ,若对任意
,若对任意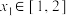 ,均存在
,均存在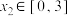 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
3 . 函数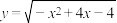 的值域是
的值域是_______________ .
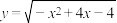 的值域是
的值域是
您最近一年使用:0次
2022-11-02更新
|
295次组卷
|
2卷引用:江西省贵溪市实验中学三校生2023届高三上学期第二次月考数学试题
解题方法
4 . 已知二次函数 满足
满足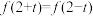 ,并且图像过点
,并且图像过点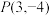 和
和 求:
求:
(1)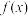 的解析式.
的解析式.
(2)当x为何值时,y有最值?
 满足
满足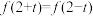 ,并且图像过点
,并且图像过点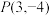 和
和 求:
求:(1)
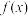 的解析式.
的解析式.(2)当x为何值时,y有最值?
您最近一年使用:0次
解题方法
5 . 函数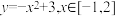 的最小值为( )
的最小值为( )
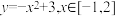 的最小值为( )
的最小值为( )A. | B.0 | C.2 | D.3 |
您最近一年使用:0次
名校
解题方法
6 . 已知全集 ,集合
,集合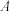 是函数
是函数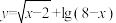 的定义域,
的定义域,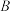 是函数
是函数 在
在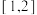 上的值域.
上的值域.
(1)求集合 ;
;
(2)求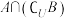 ,
,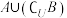 .
.
 ,集合
,集合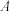 是函数
是函数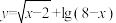 的定义域,
的定义域,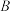 是函数
是函数 在
在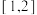 上的值域.
上的值域.(1)求集合
 ;
;(2)求
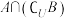 ,
,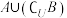 .
.
您最近一年使用:0次
2022-10-21更新
|
106次组卷
|
2卷引用:江西省鹰潭市贵溪市实验中学2023届高三上学期10月第一次月考数学(理)试题
名校
7 . 已知函数 是定义在
是定义在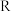 上的偶函数,当
上的偶函数,当 时,
时, 是一个二次函数的一部分,其图象如图所示.
是一个二次函数的一部分,其图象如图所示.
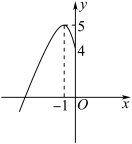
(1)求 在
在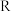 上的解析式;
上的解析式;
(2)若函数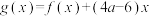 ,
, ,求
,求 的最大值.
的最大值.
 是定义在
是定义在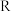 上的偶函数,当
上的偶函数,当 时,
时, 是一个二次函数的一部分,其图象如图所示.
是一个二次函数的一部分,其图象如图所示.
(1)求
 在
在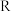 上的解析式;
上的解析式;(2)若函数
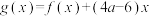 ,
, ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
2022-10-21更新
|
801次组卷
|
2卷引用:江西省鹰潭市贵溪市实验中学2023届高三上学期10月第一次月考数学(理)试题
名校
解题方法
8 . 某手机企业计划将某项新技术应用到手机生产中去,为了研究市场的反应,该企业计划用一年时间进行试产、试销.通过市场分析发现,生产此款手机全年需投入固定成本280万元,每生产x千部手机,需另投入成本 万元,且
万元,且 假设每部手机售价定为0.8万元,且全年内生产的手机当年能全部销售完.
假设每部手机售价定为0.8万元,且全年内生产的手机当年能全部销售完.
(1)求出全年的利润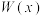 (万元)关于年产量x(千部)的函数关系式(利润=销售额-成本);
(万元)关于年产量x(千部)的函数关系式(利润=销售额-成本);
(2)当全年产量为多少千部时,该企业所获利润最大?最大利润是多少万元?
 万元,且
万元,且 假设每部手机售价定为0.8万元,且全年内生产的手机当年能全部销售完.
假设每部手机售价定为0.8万元,且全年内生产的手机当年能全部销售完.(1)求出全年的利润
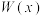 (万元)关于年产量x(千部)的函数关系式(利润=销售额-成本);
(万元)关于年产量x(千部)的函数关系式(利润=销售额-成本);(2)当全年产量为多少千部时,该企业所获利润最大?最大利润是多少万元?
您最近一年使用:0次
2022-08-31更新
|
1132次组卷
|
10卷引用:江西省瑞金市第二中学2023届高三上学期开学考数学(理)试题
江西省瑞金市第二中学2023届高三上学期开学考数学(理)试题2023版 湘教版(2019) 必修第一册 过关斩将 第3章 函数的概念与性质湖北省黄石市2022-2023学年高一上学期10月月考数学试题广东省广大附2022-2023学年高一上学期第一次月考数学试题广东省惠州市丰湖高级中学2022-2023学年高一上学期期中数学试题新疆霍城县江苏中学2024届高三上学期开学摸底考试数学试题湖南省邵阳市邵东市第一中学2022-2023学年高一下学期期中考试数学试题浙江省温州市万全综合高中2023-2024学年高一上学期期中数学试题河南省郑州市河南省实验中学2023-2024学年高一上学期12月月考数学试题广东省信宜市第二中学2023-2024学年高一上学期1月月考数学试题
9 . 已知函数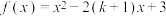 .
.
(1)若函数 为偶函数,求实数
为偶函数,求实数 的值;
的值;
(2)若函数 在区间
在区间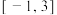 上具有单调性,求实数
上具有单调性,求实数 的取值范围;
的取值范围;
(3)求函数 在区间
在区间 上的最小值.
上的最小值.
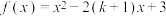 .
.(1)若函数
 为偶函数,求实数
为偶函数,求实数 的值;
的值;(2)若函数
 在区间
在区间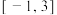 上具有单调性,求实数
上具有单调性,求实数 的取值范围;
的取值范围;(3)求函数
 在区间
在区间 上的最小值.
上的最小值.
您最近一年使用:0次
2022-08-15更新
|
987次组卷
|
3卷引用:江西省瑞金市第二中学2023届高三上学期开学考数学(文)试题
江西省瑞金市第二中学2023届高三上学期开学考数学(文)试题2023版 苏教版(2019) 必修第一册 名校名师卷 专题一、二、三滚动测试卷(已下线)第三章 函数的概念与性质(单元检测)-【同步题型讲义】(人教A版2019必修第一册)
名校
解题方法
10 . 函数 (
( 且
且 )在
)在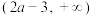 上是增函数,则
上是增函数,则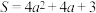 的取值范围是( )
的取值范围是( )
 (
( 且
且 )在
)在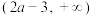 上是增函数,则
上是增函数,则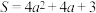 的取值范围是( )
的取值范围是( )A.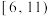 | B.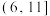 | C.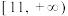 | D.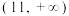 |
您最近一年使用:0次
2022-07-21更新
|
1855次组卷
|
5卷引用:江西省宜春市丰城中学2023届高三上学期入学考试数学(文)试题



