名校
解题方法
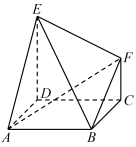
1 . 如图,四边形 是边长为2的正方形,
是边长为2的正方形,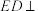 平面
平面 ,
,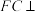 平面
平面 ,
,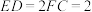 ,则四面体
,则四面体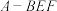 的体积为( )
的体积为( )
 是边长为2的正方形,
是边长为2的正方形,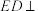 平面
平面 ,
,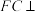 平面
平面 ,
,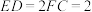 ,则四面体
,则四面体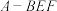 的体积为( )
的体积为( )
A. | B. | C.1 | D.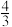 |
您最近一年使用:0次
2020-03-20更新
|
841次组卷
|
5卷引用:山东省日照市实验高级中学2023-2024学年高二上学期第二次阶段性考试(12月)数学试题
山东省日照市实验高级中学2023-2024学年高二上学期第二次阶段性考试(12月)数学试题2020届东北三省三校哈尔滨师大附中、东北师大附中、辽宁省实验中学高三第一次联合模拟考试理科数学试题(已下线)专题04 立体几何-2020年高三数学(理)3-4月模拟试题汇编(已下线)第29练 空间几何体的表面积和体积-2021年高考数学(理)一轮复习小题必刷(已下线)解密05 空间几何体的表面积和体积(讲义)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练
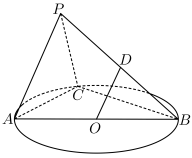
2 . 如图所示, 是
是 的直径,点
的直径,点 在
在 上,
上, 是
是 所在平面外一点,
所在平面外一点, 是
是 的中点.
的中点.
(1).求证: 平面
平面 ;
;
(2).若 是边长为6的正三角形,
是边长为6的正三角形, ,且
,且 ,求三棱锥
,求三棱锥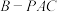 的体积.
的体积.
 是
是 的直径,点
的直径,点 在
在 上,
上, 是
是 所在平面外一点,
所在平面外一点, 是
是 的中点.
的中点.
(1).求证:
 平面
平面 ;
;(2).若
 是边长为6的正三角形,
是边长为6的正三角形, ,且
,且 ,求三棱锥
,求三棱锥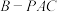 的体积.
的体积.
您最近一年使用:0次
2020-03-13更新
|
1921次组卷
|
6卷引用:山东省日照市2019—2020学年第二学期高一期末校际联合考试数学试题
名校
3 . 如图,三棱柱 中,
中, ,
, 分别为
分别为 ,
, 的中点.
的中点.
(1)证明:直线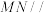 平面
平面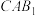 ;
;
(2)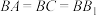 ,
, ,
,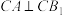 ,
, ,求平面
,求平面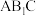 和平面
和平面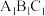 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
 中,
中, ,
, 分别为
分别为 ,
, 的中点.
的中点.
(1)证明:直线
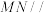 平面
平面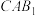 ;
;(2)
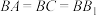 ,
, ,
,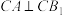 ,
, ,求平面
,求平面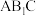 和平面
和平面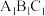 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
您最近一年使用:0次
2020-03-24更新
|
193次组卷
|
4卷引用:山东省日照市2017届高三下学期第二次模拟考试数学(理)试题
名校
解题方法
4 . 如图,菱形 与正
与正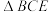 的边长均为
的边长均为 ,且平面
,且平面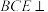 平面
平面 ,
,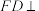 平面
平面 ,且
,且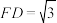 ,
,
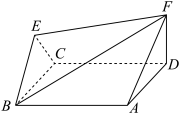
(1)求证: 平面
平面 ;
;
(2)若 ,求二面角
,求二面角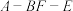 的余弦值.
的余弦值.
 与正
与正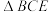 的边长均为
的边长均为 ,且平面
,且平面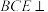 平面
平面 ,
,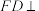 平面
平面 ,且
,且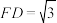 ,
,
(1)求证:
 平面
平面 ;
;(2)若
 ,求二面角
,求二面角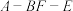 的余弦值.
的余弦值.
您最近一年使用:0次
2020-06-24更新
|
520次组卷
|
12卷引用:【市级联考】山东省日照市2017届高三下学期第一次模拟考试数学(理)试题
【市级联考】山东省日照市2017届高三下学期第一次模拟考试数学(理)试题2016届河北省冀州市中学高三上学期一轮复习一理科数学试卷2016届重庆一中高三下学期3月月考理科数学试卷2016届安徽六安一中高三下组卷四理科数学试卷2016-2017学年河北定州中学高二上期7.8周练数学试卷河北省武邑中学2016-2017学年高二下学期期中考试数学(理)试题山东省济南外国语学校三箭分校2016-2017学年高二下学期期末考试数学(理)试题2019届湖南省岳阳市第一中学高三第六次质检数学(理)试题浙江省宁波市鄞州中学2020届高三下学期高考冲刺考试数学试题甘肃省张掖市2021-2022学年高三上学期期末数学(理)试题河南省温县第一高级中学2021-2022学年高三下学期3月月考理科数学试题河南省顶尖名校2021-2022学年高三下学期第二次素养调研理科数学试题
5 . 如图,直三棱柱ABC-A1B1C1中,AC=6,AB=10,BC=8,AA1=8,点D是AB的中点.

(Ⅰ)求证:AC1∥平面CDB1
(Ⅱ)求三棱锥B-CDB1的体积.

(Ⅰ)求证:AC1∥平面CDB1
(Ⅱ)求三棱锥B-CDB1的体积.
您最近一年使用:0次
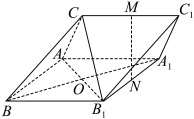
6 . 如图,四棱锥 中,
中, ,底面
,底面 是梯形,AB∥CD,
是梯形,AB∥CD, ,AB=PD=4,CD=2,
,AB=PD=4,CD=2,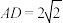 ,M为CD的中点,N为PB上一点,且
,M为CD的中点,N为PB上一点,且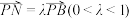 .
.
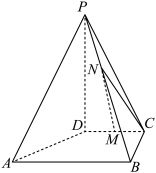
(1)若 MN∥平面PAD;
MN∥平面PAD;
(2)若直线AN与平面PBC所成角的正弦值为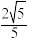 ,求异面直线AD与直线CN所成角的余弦值.
,求异面直线AD与直线CN所成角的余弦值.
 中,
中, ,底面
,底面 是梯形,AB∥CD,
是梯形,AB∥CD, ,AB=PD=4,CD=2,
,AB=PD=4,CD=2,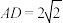 ,M为CD的中点,N为PB上一点,且
,M为CD的中点,N为PB上一点,且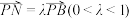 .
.
(1)若
 MN∥平面PAD;
MN∥平面PAD;(2)若直线AN与平面PBC所成角的正弦值为
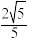 ,求异面直线AD与直线CN所成角的余弦值.
,求异面直线AD与直线CN所成角的余弦值.
您最近一年使用:0次
2018-06-07更新
|
702次组卷
|
8卷引用:山东省日照市国开中学2023-2024学年高二上学期第一次月考数学试题
山东省日照市国开中学2023-2024学年高二上学期第一次月考数学试题江西省重点中学协作体2018届高三下学期第一次联考数学(理)试题河北省武邑中学2018届高三下学期开学考试数学(理)试题(已下线)2018年5月29日 押高考数学第18题——《每日一题》2018年高三理科数学四轮复习(已下线)《高频考点解密》—解密16 空间向量与立体几何人教B版(2019) 选择性必修第一册 过关斩将 第一章 空间向量与立体几何 本章达标检测(已下线)解密15 空间向量与立体几何 (讲义)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练山东省威海市乳山市银滩高级中学2023-2024学年高二上学期9月月考数学试题
7 . 直三棱柱 中,
中, ,
, ,
,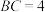 ,点
,点 是线段
是线段 上的动点.
上的动点.
(1)当点 是
是 的中点时,求证:
的中点时,求证: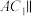 平面
平面 ;
;
(2)线段 上是否存在点
上是否存在点 ,使得平面
,使得平面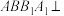 平面
平面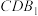 ?若存在,试求出
?若存在,试求出 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.

 中,
中, ,
, ,
,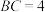 ,点
,点 是线段
是线段 上的动点.
上的动点.(1)当点
 是
是 的中点时,求证:
的中点时,求证: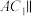 平面
平面 ;
;(2)线段
 上是否存在点
上是否存在点 ,使得平面
,使得平面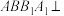 平面
平面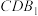 ?若存在,试求出
?若存在,试求出 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
您最近一年使用:0次
2018-03-02更新
|
720次组卷
|
5卷引用:山东省日照市2018-2019学年高一上学期期末数学试题
8 . 如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,∠DAB=60°.
(1)求证:直线AM∥平面PNC;
(2)求二面角D﹣PC﹣N的余弦值.

(1)求证:直线AM∥平面PNC;
(2)求二面角D﹣PC﹣N的余弦值.

您最近一年使用:0次
2018-01-12更新
|
613次组卷
|
3卷引用:山东省日照市2019-2020学年高二上学期期末数学试题
名校
9 . 如图,菱 与四边形
与四边形 相交于
相交于 ,
,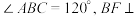 平面
平面 ,
, 为
为 的中点,
的中点,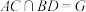 .
.

(1)求证: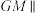 平面
平面 ;
;
(2)求直线 与平面
与平面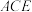 成角的正弦值.
成角的正弦值.
 与四边形
与四边形 相交于
相交于 ,
,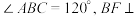 平面
平面 ,
, 为
为 的中点,
的中点,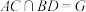 .
.
(1)求证:
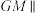 平面
平面 ;
;(2)求直线
 与平面
与平面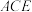 成角的正弦值.
成角的正弦值.
您最近一年使用:0次
2017-06-02更新
|
763次组卷
|
5卷引用:山东省日照市2017届高三第三次模拟考试数学理试题
解题方法
10 . 如图,菱形 与四边形
与四边形 相交于
相交于 ,
,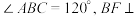 平面
平面 ,
, ∥
∥ ,
,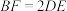 ,
, ,
, 为
为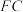 的中点,
的中点,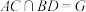 .
.
(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面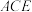 ⊥平面
⊥平面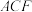 .
.
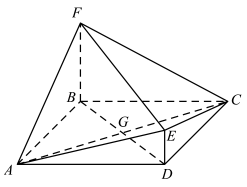
 与四边形
与四边形 相交于
相交于 ,
,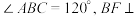 平面
平面 ,
, ∥
∥ ,
,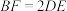 ,
, ,
, 为
为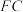 的中点,
的中点,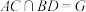 .
.(1)求证:
 ∥平面
∥平面 ;
;(2)求证:平面
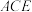 ⊥平面
⊥平面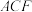 .
.
您最近一年使用:0次
2017-06-01更新
|
826次组卷
|
2卷引用:山东省日照市2017届高三校际联合模拟考试(三模)数学(文)试题



