解题方法
1 . 已知以坐标原点 为圆心的圆与抛物线
为圆心的圆与抛物线 :
: 相交于不同的两点
相交于不同的两点 ,与抛物线
,与抛物线 的准线相交于不同的两点
的准线相交于不同的两点 ,且
,且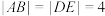 .
.
(1)求抛物线 的方程;
的方程;
(2)若不经过坐标原点 的直线
的直线 与抛物线
与抛物线 相交于不同的两点
相交于不同的两点 、
、 ,且满足
,且满足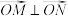 ,证明直线
,证明直线 过定点
过定点 ,并求出点
,并求出点 的坐标.
的坐标.
 为圆心的圆与抛物线
为圆心的圆与抛物线 :
: 相交于不同的两点
相交于不同的两点 ,与抛物线
,与抛物线 的准线相交于不同的两点
的准线相交于不同的两点 ,且
,且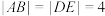 .
.(1)求抛物线
 的方程;
的方程;(2)若不经过坐标原点
 的直线
的直线 与抛物线
与抛物线 相交于不同的两点
相交于不同的两点 、
、 ,且满足
,且满足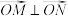 ,证明直线
,证明直线 过定点
过定点 ,并求出点
,并求出点 的坐标.
的坐标.
您最近一年使用:0次
2022-12-17更新
|
427次组卷
|
2卷引用:四川省成都市简阳市阳安中学2022-2023学年高二上学期12月月考数学(理)试题
名校
解题方法
2 . 设抛物线 的准线为l,A、B为抛物线上两动点,
的准线为l,A、B为抛物线上两动点,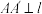 于
于 ,定点
,定点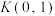 使
使 有最小值
有最小值 .
.
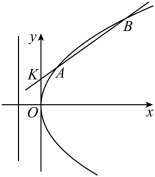
(1)求抛物线的方程;
(2)当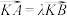 (
(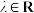 且
且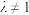 )时,是否存在一定点T满足
)时,是否存在一定点T满足 为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
 的准线为l,A、B为抛物线上两动点,
的准线为l,A、B为抛物线上两动点,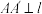 于
于 ,定点
,定点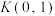 使
使 有最小值
有最小值 .
.
(1)求抛物线的方程;
(2)当
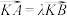 (
(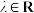 且
且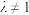 )时,是否存在一定点T满足
)时,是否存在一定点T满足 为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
您最近一年使用:0次
2022-12-04更新
|
1675次组卷
|
10卷引用:四川省成都市第七中学2022-2023学年高二上学期期中数学理科试题
四川省成都市第七中学2022-2023学年高二上学期期中数学理科试题四川省成都市成都市第七中学2022-2023学年高二上学期期中数学文科试题四川省成都市树德中学2022-2023学年高二上学期期中考试数学(理)试题云南省大理市下关第一中学教育集团2022~2023学年高二上学期段考(二)数学试题(A卷)云南省下关第一中学2022-2023学年高二上学期段考(二)数学(A卷)试题辽宁省沈阳市东北育才双语学校2022-2023学年高二上学期期末数学试题(已下线)专题04 圆锥曲线经典题型全归纳(2)广西壮族自治区南宁市第三中学2023届高三模拟数学(理)试题(二)湖南省长沙市长郡中学2023-2024学年高二上学期期中数学试题(已下线)3.3.2 抛物线的简单几何性质【第三课】“上好三节课,做好三套题“高中数学素养晋级之路
名校
解题方法
3 . 已知抛物线 过点
过点 ,
, 为原点.
为原点.
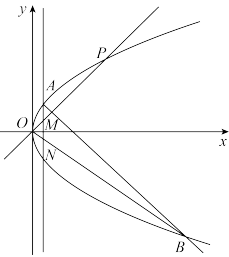
(1)求抛物线 的方程,并求其焦点坐标和准线方程;
的方程,并求其焦点坐标和准线方程;
(2)直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 、
、 (
( 、
、 不与
不与 重合).过点
重合).过点 作
作 轴的垂线分别与直线
轴的垂线分别与直线 、
、 交于点
交于点 、
、 ,且
,且 为线段
为线段 的中点.试判断直线
的中点.试判断直线 是否过定点?若是,求出该定点;若不是,说明理由.
是否过定点?若是,求出该定点;若不是,说明理由.
 过点
过点 ,
, 为原点.
为原点.
(1)求抛物线
 的方程,并求其焦点坐标和准线方程;
的方程,并求其焦点坐标和准线方程;(2)直线
 与抛物线
与抛物线 交于不同的两点
交于不同的两点 、
、 (
( 、
、 不与
不与 重合).过点
重合).过点 作
作 轴的垂线分别与直线
轴的垂线分别与直线 、
、 交于点
交于点 、
、 ,且
,且 为线段
为线段 的中点.试判断直线
的中点.试判断直线 是否过定点?若是,求出该定点;若不是,说明理由.
是否过定点?若是,求出该定点;若不是,说明理由.
您最近一年使用:0次
2022-11-28更新
|
467次组卷
|
2卷引用:四川省成都市树德中学2022-2023学年高二上学期11月阶段性测试数学试题
4 . 已知抛物线C: 的焦点为F,过点P(0,2)的动直线l与抛物线相交于A,B两点.当l经过点F时,点A恰好为线段PF中点.
的焦点为F,过点P(0,2)的动直线l与抛物线相交于A,B两点.当l经过点F时,点A恰好为线段PF中点.
(1)求p的值;
(2)是否存在定点T, 使得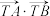 为常数? 若存在,求出点T的坐标及该常数; 若不存在,说明理由.
为常数? 若存在,求出点T的坐标及该常数; 若不存在,说明理由.
 的焦点为F,过点P(0,2)的动直线l与抛物线相交于A,B两点.当l经过点F时,点A恰好为线段PF中点.
的焦点为F,过点P(0,2)的动直线l与抛物线相交于A,B两点.当l经过点F时,点A恰好为线段PF中点.(1)求p的值;
(2)是否存在定点T, 使得
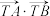 为常数? 若存在,求出点T的坐标及该常数; 若不存在,说明理由.
为常数? 若存在,求出点T的坐标及该常数; 若不存在,说明理由.
您最近一年使用:0次
2022-09-08更新
|
937次组卷
|
4卷引用:四川省成都外国语学校2022-2023学年高二上学期12月月考数学(文)试题
四川省成都外国语学校2022-2023学年高二上学期12月月考数学(文)试题四川省成都外国语学校2022-2023学年高二上学期12月月考数学(理)试题江苏省南京市2022-2023学年高三上学期9月学情调研数学试题(已下线)专题3.13 直线与抛物线的位置关系-重难点题型精讲-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)
名校
5 . 已知曲线C:x2=2y,点D为直线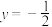 上的动点,过点D作C的两条切线,切点分别为A,B.
上的动点,过点D作C的两条切线,切点分别为A,B.
(1)若点D的坐标为 ,求这两条切线的方程;
,求这两条切线的方程;
(2)证明:直线AB过定点.
 上的动点,过点D作C的两条切线,切点分别为A,B.
上的动点,过点D作C的两条切线,切点分别为A,B.(1)若点D的坐标为
 ,求这两条切线的方程;
,求这两条切线的方程;(2)证明:直线AB过定点.
您最近一年使用:0次
2022-03-26更新
|
329次组卷
|
3卷引用:四川省成都市双流区棠湖中学2021-2022学年高二下学期3月月考数学(文)试题
四川省成都市双流区棠湖中学2021-2022学年高二下学期3月月考数学(文)试题四川省成都市双流区棠湖中学2021-2022学年高二下学期3月月考数学(理)试题(已下线)第16讲 直线和圆锥曲线的位置关系(2)
名校
解题方法
6 . 动圆P与直线 相切,点
相切,点 在动圆上.
在动圆上.
(1)求圆心P的轨迹Q的方程;
(2)过点F作曲线O的两条互相垂直的弦AB,CD,设AB,CD的中点分别为M,N,求证:直线MN必过定点.
 相切,点
相切,点 在动圆上.
在动圆上.(1)求圆心P的轨迹Q的方程;
(2)过点F作曲线O的两条互相垂直的弦AB,CD,设AB,CD的中点分别为M,N,求证:直线MN必过定点.
您最近一年使用:0次
2022-04-08更新
|
1023次组卷
|
8卷引用:四川省成都市新津中学2021-2022学年高二下学期5月月考数学(文)试题
名校
解题方法
7 . 已知圆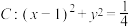 ,一动圆与直线
,一动圆与直线 相切且与圆C外切.
相切且与圆C外切.
(1)求动圆圆心P的轨迹T的方程;
(2)若经过定点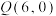 的直线l与曲线
的直线l与曲线 相交于
相交于 两点,M是线段
两点,M是线段 的中点,过
的中点,过 作
作 轴的平行线与曲线
轴的平行线与曲线 相交于点
相交于点 ,试问是否存在直线l,使得
,试问是否存在直线l,使得 ,若存在,求出直线l的方程;若不存在,说明理由.
,若存在,求出直线l的方程;若不存在,说明理由.
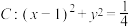 ,一动圆与直线
,一动圆与直线 相切且与圆C外切.
相切且与圆C外切.(1)求动圆圆心P的轨迹T的方程;
(2)若经过定点
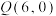 的直线l与曲线
的直线l与曲线 相交于
相交于 两点,M是线段
两点,M是线段 的中点,过
的中点,过 作
作 轴的平行线与曲线
轴的平行线与曲线 相交于点
相交于点 ,试问是否存在直线l,使得
,试问是否存在直线l,使得 ,若存在,求出直线l的方程;若不存在,说明理由.
,若存在,求出直线l的方程;若不存在,说明理由.
您最近一年使用:0次
2023-09-02更新
|
585次组卷
|
9卷引用:四川省成都市双流中学2022-2023学年高三上学期适应性数学(理科)试题
四川省成都市双流中学2022-2023学年高三上学期适应性数学(理科)试题江苏省南通市海安高级中学2022-2023学年高二上学期11月期中数学试题(已下线)第09讲 第八章 平面解析几何 (基础拿分卷)2017届广东深圳市高三第二次(4月)调研考试数学文试卷2020届山西省太原市第五中学高三下学期4月模拟数学(理)试题(已下线)3.3 抛物线-2021-2022学年高二数学尖子生同步培优题典(人教A版2019选择性必修第一册)江苏省南京航天航空大学附属高级中学2022-2023学年高二下学期3月月考数学试题(已下线)专题11 圆锥曲线(4大易错点分析+解题模板+举一反三+易错题通关)(已下线)模块三 专题5 大题分类练(解析几何)拔高能力练
名校
解题方法
8 . 设抛物线 的焦点为
的焦点为 ,过焦点
,过焦点 作直线
作直线 交抛物线
交抛物线 于
于 ,
, 两点.
两点.
(1)若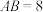 ,求直线
,求直线 的方程;
的方程;
(2)设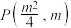 为抛物线
为抛物线 上异于
上异于 ,
, 的任意一点,直线
的任意一点,直线 ,
, 分别与抛物线
分别与抛物线 的准线相交于
的准线相交于 ,
, 两点,求证:以线段
两点,求证:以线段 为直径的圆经过
为直径的圆经过 轴上的定点.
轴上的定点.
 的焦点为
的焦点为 ,过焦点
,过焦点 作直线
作直线 交抛物线
交抛物线 于
于 ,
, 两点.
两点.(1)若
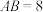 ,求直线
,求直线 的方程;
的方程;(2)设
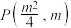 为抛物线
为抛物线 上异于
上异于 ,
, 的任意一点,直线
的任意一点,直线 ,
, 分别与抛物线
分别与抛物线 的准线相交于
的准线相交于 ,
, 两点,求证:以线段
两点,求证:以线段 为直径的圆经过
为直径的圆经过 轴上的定点.
轴上的定点.
您最近一年使用:0次
2021-11-22更新
|
584次组卷
|
6卷引用:四川省成都市第二十中学校2022-2023学年高三上学期期中数学试题
四川省成都市第二十中学校2022-2023学年高三上学期期中数学试题(已下线)解密16 抛物线方程(分层训练)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(新高考专用)(已下线)专题4 圆锥曲线的综合应用-学会解题之高三数学321训练体系【2022版】(已下线)考点23圆锥曲线综合应用-1-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)四川省成都市石室中学2021-2022学年高三上学期期中考试数学(理)试题四川省遂宁市遂宁市第二中学校2021-2022学年高三上学期期中数学(理)试题



