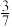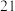1 . 如图,在 中,
中, ,
,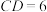 ,
,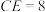 ,
, 为
为 的中点;
的中点; 与过
与过 点的直线
点的直线 交于
交于 ,直线
,直线 和
和 的延长线交于点
的延长线交于点 ,
,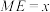 ,
, .
.
完成下面的填空: 作
作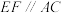 交直线
交直线 于
于 点.
点.
(1) 是______三角形;
是______三角形;
(2)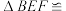 ______,
______, ______,则
______,则 关于
关于 的表达式______(
的表达式______(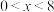 ).
).
完成下面的解答过程:
(3) 列表:
列表:
根据( )中所求函数关系式计算并补全表格
)中所求函数关系式计算并补全表格
 描点:根据表中数值,继续描出①中剩余的三个点
描点:根据表中数值,继续描出①中剩余的三个点 ;
;
 连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象;
连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象; 绕
绕 点旋转与直线
点旋转与直线 相交于点
相交于点 ,当
,当 取什么值时,
取什么值时,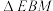 和
和 相似?
相似?
 中,
中, ,
,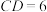 ,
,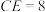 ,
, 为
为 的中点;
的中点; 与过
与过 点的直线
点的直线 交于
交于 ,直线
,直线 和
和 的延长线交于点
的延长线交于点 ,
,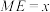 ,
, .
.完成下面的填空:
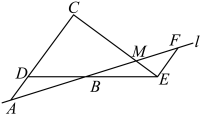
 作
作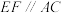 交直线
交直线 于
于 点.
点.(1)
 是______三角形;
是______三角形;(2)
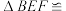 ______,
______, ______,则
______,则 关于
关于 的表达式______(
的表达式______(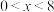 ).
).完成下面的解答过程:
(3)
 列表:
列表:根据(
 )中所求函数关系式计算并补全表格
)中所求函数关系式计算并补全表格
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
| … |
 描点:根据表中数值,继续描出①中剩余的三个点
描点:根据表中数值,继续描出①中剩余的三个点 ;
;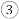 连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象;
连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象;
 绕
绕 点旋转与直线
点旋转与直线 相交于点
相交于点 ,当
,当 取什么值时,
取什么值时,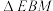 和
和 相似?
相似?
您最近一年使用:0次
2 .  的
的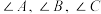 所对边分别是a,b,c,若满足
所对边分别是a,b,c,若满足 ,则称
,则称 为类勾股三角形,边c称为该三角形的勾股边.
为类勾股三角形,边c称为该三角形的勾股边. 是类勾股三角形,
是类勾股三角形, 为勾股边,且
为勾股边,且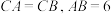 ,
, 是中线,求
是中线,求 的长;
的长;
【深入探究】如图2, 是
是 的中线,若
的中线,若 是以
是以 为勾股边的类勾股三角形,①分别过A,B作
为勾股边的类勾股三角形,①分别过A,B作 的垂线,垂足分别为E,F,求证
的垂线,垂足分别为E,F,求证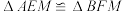
②试判断 与
与 的数量关系并证明;
的数量关系并证明;
【结论应用】如图3,在四边形 中,
中,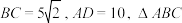 与
与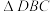 都是以
都是以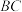 为勾股边的类勾股三角形,M,N分别为
为勾股边的类勾股三角形,M,N分别为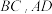 的中点,求线段
的中点,求线段 的长.
的长.
 的
的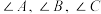 所对边分别是a,b,c,若满足
所对边分别是a,b,c,若满足 ,则称
,则称 为类勾股三角形,边c称为该三角形的勾股边.
为类勾股三角形,边c称为该三角形的勾股边.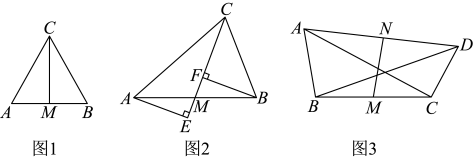
 是类勾股三角形,
是类勾股三角形, 为勾股边,且
为勾股边,且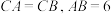 ,
, 是中线,求
是中线,求 的长;
的长;【深入探究】如图2,
 是
是 的中线,若
的中线,若 是以
是以 为勾股边的类勾股三角形,①分别过A,B作
为勾股边的类勾股三角形,①分别过A,B作 的垂线,垂足分别为E,F,求证
的垂线,垂足分别为E,F,求证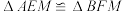
②试判断
 与
与 的数量关系并证明;
的数量关系并证明;【结论应用】如图3,在四边形
 中,
中,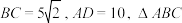 与
与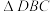 都是以
都是以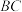 为勾股边的类勾股三角形,M,N分别为
为勾股边的类勾股三角形,M,N分别为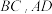 的中点,求线段
的中点,求线段 的长.
的长.
您最近一年使用:0次
2024-01-29更新
|
313次组卷
|
2卷引用:江西省/抚州市2023-2024学年八年级上学期期末数学试题
解题方法
3 . 在 中,
中, ,
,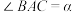 ,点
,点 是平面内不与点
是平面内不与点 ,
, 重合的任意一点,连接
重合的任意一点,连接 ,将线段
,将线段 绕点
绕点 旋转
旋转 得到线段
得到线段 ,连接
,连接 、
、 、
、 .
.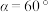 时,
时,
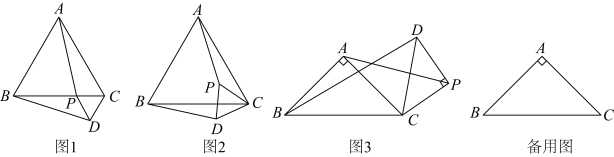
①如图1,当点 在
在 的边
的边 上时,线段
上时,线段 绕点
绕点 顺时针旋转
顺时针旋转 得到线段
得到线段 ,则
,则 与
与 的数量关系是_______________;
的数量关系是_______________;
②如图2,当点 在
在 内部时,线段
内部时,线段 绕点
绕点 顺时针旋转
顺时针旋转 得到线段
得到线段 ,①中
,①中 与
与 的数量关系还成立吗?若成立,请证明结论,若不成立,说明理由;
的数量关系还成立吗?若成立,请证明结论,若不成立,说明理由;
(2)当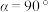 时,
时,
①如图3,线段 绕点
绕点 顺时针旋转
顺时针旋转 得到线段
得到线段 .试判断
.试判断 与
与 的数量关系,并说明理由;
的数量关系,并说明理由;
②若点 ,
, ,
, 在一条直线上,且
在一条直线上,且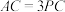 ,线段
,线段 绕点
绕点
逆时针 旋转 得到线段
得到线段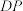 ,求
,求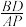 的值.
的值.
 中,
中, ,
,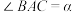 ,点
,点 是平面内不与点
是平面内不与点 ,
, 重合的任意一点,连接
重合的任意一点,连接 ,将线段
,将线段 绕点
绕点 旋转
旋转 得到线段
得到线段 ,连接
,连接 、
、 、
、 .
.
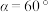 时,
时, ①如图1,当点
 在
在 的边
的边 上时,线段
上时,线段 绕点
绕点 顺时针旋转
顺时针旋转 得到线段
得到线段 ,则
,则 与
与 的数量关系是_______________;
的数量关系是_______________;②如图2,当点
 在
在 内部时,线段
内部时,线段 绕点
绕点 顺时针旋转
顺时针旋转 得到线段
得到线段 ,①中
,①中 与
与 的数量关系还成立吗?若成立,请证明结论,若不成立,说明理由;
的数量关系还成立吗?若成立,请证明结论,若不成立,说明理由;(2)当
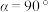 时,
时,①如图3,线段
 绕点
绕点 顺时针旋转
顺时针旋转 得到线段
得到线段 .试判断
.试判断 与
与 的数量关系,并说明理由;
的数量关系,并说明理由;②若点
 ,
, ,
, 在一条直线上,且
在一条直线上,且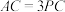 ,线段
,线段 绕点
绕点
 得到线段
得到线段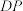 ,求
,求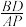 的值.
的值.
您最近一年使用:0次
2023-08-15更新
|
319次组卷
|
3卷引用:江西省抚州高新技术产业开发区梦湖学校2022-2023学年九年级下学期月考数学试题
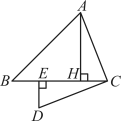
4 . 如图, 中,
中, ,
,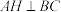 于点H,
于点H, ,
,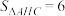 ,过点C作
,过点C作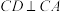 且
且 ,
, 于点E,则
于点E,则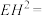
______
 中,
中, ,
,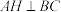 于点H,
于点H, ,
,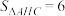 ,过点C作
,过点C作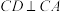 且
且 ,
, 于点E,则
于点E,则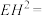

您最近一年使用:0次
名校
5 . 如图,在梯形 中,
中,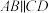 ,
,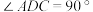 ,过
,过 点作
点作 于
于 ,过
,过 点作
点作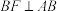 交
交 于
于 ,连接
,连接 .
.

(1)若 平分
平分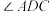 ,
, ,
, ,求四边形
,求四边形 的面积;
的面积;
(2)若 ,求证:
,求证: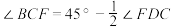 .
.
 中,
中,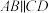 ,
,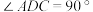 ,过
,过 点作
点作 于
于 ,过
,过 点作
点作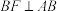 交
交 于
于 ,连接
,连接 .
.
(1)若
 平分
平分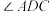 ,
, ,
, ,求四边形
,求四边形 的面积;
的面积;(2)若
 ,求证:
,求证: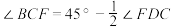 .
.
您最近一年使用:0次
6 . 综合与探究:
如图1所示的是由两块三角板组成的图形,其中在 中,
中,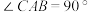 ,
,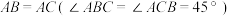 ,在
,在 中,
中,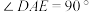 ,
,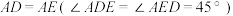 ,点B,E,D在同一条直线上,AC与BD交于点F,连接CD并延长,交BA的延长线于点G.
,点B,E,D在同一条直线上,AC与BD交于点F,连接CD并延长,交BA的延长线于点G.

(1)当 时,试用含
时,试用含 的代数式表示∠BAE的度数.
的代数式表示∠BAE的度数.
(2)当 时,试探究BC与BG的数量关系,并说明理由.
时,试探究BC与BG的数量关系,并说明理由.
(3)过点C作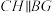 ,交BD的延长线于点H,如图2所示,在满足(2)的情况下,求∠DCH的度数,并直接写出与∠DCH相等的角(除∠G外,写两个即可).
,交BD的延长线于点H,如图2所示,在满足(2)的情况下,求∠DCH的度数,并直接写出与∠DCH相等的角(除∠G外,写两个即可).
如图1所示的是由两块三角板组成的图形,其中在
 中,
中,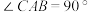 ,
,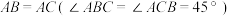 ,在
,在 中,
中,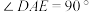 ,
,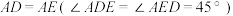 ,点B,E,D在同一条直线上,AC与BD交于点F,连接CD并延长,交BA的延长线于点G.
,点B,E,D在同一条直线上,AC与BD交于点F,连接CD并延长,交BA的延长线于点G.
(1)当
 时,试用含
时,试用含 的代数式表示∠BAE的度数.
的代数式表示∠BAE的度数.(2)当
 时,试探究BC与BG的数量关系,并说明理由.
时,试探究BC与BG的数量关系,并说明理由.(3)过点C作
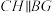 ,交BD的延长线于点H,如图2所示,在满足(2)的情况下,求∠DCH的度数,并直接写出与∠DCH相等的角(除∠G外,写两个即可).
,交BD的延长线于点H,如图2所示,在满足(2)的情况下,求∠DCH的度数,并直接写出与∠DCH相等的角(除∠G外,写两个即可).
您最近一年使用:0次
2022-08-18更新
|
1678次组卷
|
5卷引用:江西省抚州市宜黄县2021-2022学年七年级下学期阶段评估(二)数学试题
江西省抚州市宜黄县2021-2022学年七年级下学期阶段评估(二)数学试题(已下线)专题12.46 《全等三角形》挑战综合(压轴)题分类专题(专项练习)-2022-2023学年八年级数学上册基础知识专项讲练(人教版)(已下线)第十二章 全等三角形 章末检测卷-2022-2023学年八年级数学上册重难题型全归纳及技巧提升专项精练(人教版)(已下线)专题1.70 《三角形的初步知识》挑战综合(压轴)题分类专题(二)(专项练习)-2022-2023学年八年级数学上册基础知识专项讲练(浙教版)(已下线)数学(全国通用卷)-学易金卷:2023年中考第一次模拟考试卷
名校
7 . 如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE ⊥DE ,则△BDC通过下列变换能与△ACE重合的是( )

| A.绕点C逆时针旋转90度 | B.沿AB的垂直平分线翻折 |
| C.绕AB的中点M顺时针旋转90度 | D.沿DE方向平移 |
您最近一年使用:0次
2022-07-20更新
|
322次组卷
|
7卷引用:江西省抚州市黎川县黎川一中片区八校联考2023-2024学年八年级下学期期中数学试题
江西省抚州市黎川县黎川一中片区八校联考2023-2024学年八年级下学期期中数学试题山东省烟台市招远市2021-2022学年八年级上学期期末数学试题(已下线)广东省深圳市罗湖区深圳中学2021-2022学年八年级下学期期中数学试题广东省深圳市部分学校2021-2022学年八年级下学期期中数学试题(B卷)广东省深圳市部分学校2021-2022学年八年级下学期期中数学试题(A卷)(已下线)期中押题密卷01(北师大版,第1-4章)-2023-2024学年八年级数学下学期期中考点大串讲(北师大版)海南省海口市国兴中学2023-2024学年八年级下学期4月月考数学B试题
真题
名校
8 . 某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形 和等腰直角三角形
和等腰直角三角形 ,按如图1的方式摆放,
,按如图1的方式摆放, ,随后保持
,随后保持 不动,将
不动,将 绕点C按逆时针方向旋转
绕点C按逆时针方向旋转 (
( ),连接
),连接 ,
, ,延长
,延长 交
交 于点F,连接
于点F,连接 .该数学兴趣小组进行如下探究,请你帮忙解答:
.该数学兴趣小组进行如下探究,请你帮忙解答: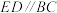 时,则
时,则 _____;
_____;
(2)【初步探究】如图3,当点E,F重合时,请直接写出 ,
, ,
, 之间的数量关系:_________;
之间的数量关系:_________;
(3)【深入探究】如图4,当点E,F不重合时,(2)中的结论是否仍然成立?若成立,请给出推理过程;若不成立,请说明理由.
(4)【拓展延伸】如图5,在 与
与 中,
中,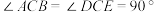 ,若
,若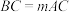 ,
,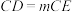 (m为常数).保持
(m为常数).保持 不动,将
不动,将 绕点C按逆时针方向旋转
绕点C按逆时针方向旋转 (
( ),连接
),连接 ,
, ,延长
,延长 交
交 于点F,连接
于点F,连接 ,如图6.试探究
,如图6.试探究 ,
, ,
, 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
 和等腰直角三角形
和等腰直角三角形 ,按如图1的方式摆放,
,按如图1的方式摆放, ,随后保持
,随后保持 不动,将
不动,将 绕点C按逆时针方向旋转
绕点C按逆时针方向旋转 (
( ),连接
),连接 ,
, ,延长
,延长 交
交 于点F,连接
于点F,连接 .该数学兴趣小组进行如下探究,请你帮忙解答:
.该数学兴趣小组进行如下探究,请你帮忙解答: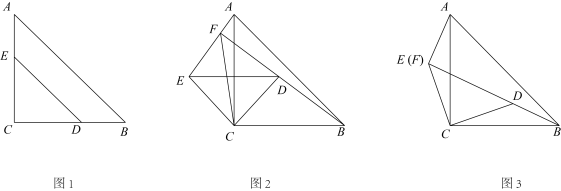
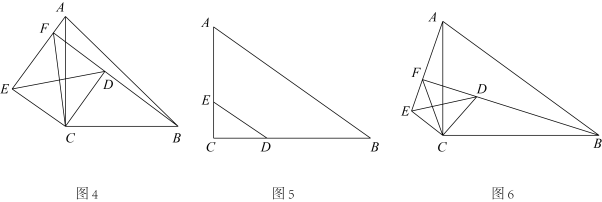
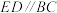 时,则
时,则 _____;
_____;(2)【初步探究】如图3,当点E,F重合时,请直接写出
 ,
, ,
, 之间的数量关系:_________;
之间的数量关系:_________;(3)【深入探究】如图4,当点E,F不重合时,(2)中的结论是否仍然成立?若成立,请给出推理过程;若不成立,请说明理由.
(4)【拓展延伸】如图5,在
 与
与 中,
中,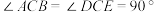 ,若
,若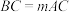 ,
,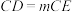 (m为常数).保持
(m为常数).保持 不动,将
不动,将 绕点C按逆时针方向旋转
绕点C按逆时针方向旋转 (
( ),连接
),连接 ,
, ,延长
,延长 交
交 于点F,连接
于点F,连接 ,如图6.试探究
,如图6.试探究 ,
, ,
, 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
您最近一年使用:0次
2022-06-16更新
|
2110次组卷
|
22卷引用:江西省抚州市金溪县第一中学2022-2023学年九年级上学期第三次月考数学试题
江西省抚州市金溪县第一中学2022-2023学年九年级上学期第三次月考数学试题江西省 抚州市 临川区江西省抚州市第一中学2023-2024年九年级上学期第二次月考数学试题2022年四川省达州市中考数学真题(已下线)专题17 图形变换(平移、旋转、对称)-2022年中考数学真题分项汇编(全国通用)(第1期)(已下线)专题09 图形的平移、对称、旋转与相似-2022年中考数学真题分项汇编 (四川专用)(已下线)专题14 相似三角形与全等三角形-三年(2020-2022)中考数学真题分项汇编(四川专用)(已下线)2022年四川省广元市中考数学变式题22-26(已下线)2022年四川省乐山市中考数学真题变式汇编22-26(已下线)专题4.54 《图形的相似》挑战综合(压轴)题分类专题(专项练习)-2022-2023学年九年级数学上册基础知识专项讲练(北师大版)(已下线)第30课 相似三角形(动态几何,坐标问题)-2022-2023学年九年级数学上册课后培优分级练(北师大版)四川省达州市开江县永兴中学2022-2023学年九年级上学期11月月考数学试题(已下线)2022年四川省达州市中考数学真题变式题21-25题(已下线)专题27.49 《相似》挑战综合(压轴)题分类专题(专项练习)-2022-2023学年九年级数学下册基础知识专项讲练(人教版)(已下线)专题6.52 《图形的相似》挑战综合(压轴)题分类专题(专项练习)-2022-2023学年九年级数学下册基础知识专项讲练(苏科版)(已下线)第五节 图形的旋转与位似03综合测(已下线)黄金卷08(青岛专用)-【赢在中考·黄金8卷】备战2023年中考数学全真模拟卷(已下线)专题23 几何综合-学易金卷:三年(2021-2023)中考数学真题分项汇编(四川专用)2023年甘肃省平凉市初中毕业与高中招生数学模拟预测试题2024年山东省济南市天桥区九年级下学期中考一模数学模拟试题2024年山东省菏泽市鲁西新区中考三模数学试题2024年山东省临沂初中学业水平考试模拟试题(一) 2024年福建省莆田市城厢区哲理中学校中考模拟数学试题
9 . 问题探究:
(1)在图1和图2中,AB CD,AD⊥BC于点O.
CD,AD⊥BC于点O.
①如图1,若点O是BC的中点,AD=6,BC=8,则AD2=____,BC2=____,(AB+CD)2=_____;
②如图2,AO:DO=1:3,AO=3,BO=4,则AD2=_____,BC2=_____,(AB+CD)2=_____;
(2)请你观察(1)中的计算结果,猜想AD2,BC2,(AB+CD)2三者之间的关系.
归纳证明:
(3)请利用图2证明你发现的关系式;
应用结论:
(4)如图3,在矩形ABCD中,E,F两点均在AD边上,BE⊥CF交于G点,EF:BE=1:4,CF=3,BC=4.求证:CG=CD;
拓展应用:
(5)如图4,已知BD为△ABC的中线,CE⊥BD交AB于点E,交BD于点F,AE=5,BD=10,EC=15,求BC的长.

(1)在图1和图2中,AB
 CD,AD⊥BC于点O.
CD,AD⊥BC于点O.①如图1,若点O是BC的中点,AD=6,BC=8,则AD2=____,BC2=____,(AB+CD)2=_____;
②如图2,AO:DO=1:3,AO=3,BO=4,则AD2=_____,BC2=_____,(AB+CD)2=_____;
(2)请你观察(1)中的计算结果,猜想AD2,BC2,(AB+CD)2三者之间的关系.
归纳证明:
(3)请利用图2证明你发现的关系式;
应用结论:
(4)如图3,在矩形ABCD中,E,F两点均在AD边上,BE⊥CF交于G点,EF:BE=1:4,CF=3,BC=4.求证:CG=CD;
拓展应用:
(5)如图4,已知BD为△ABC的中线,CE⊥BD交AB于点E,交BD于点F,AE=5,BD=10,EC=15,求BC的长.

您最近一年使用:0次
解题方法
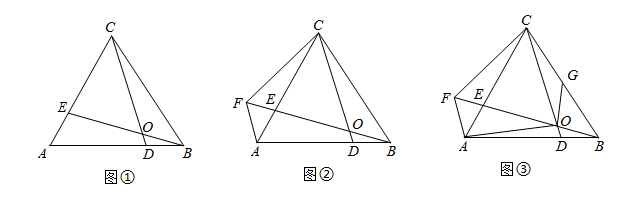
10 . 如图①,在等边△ABC中,点D、E分别是AB、AC上的点,BD=AE,BE与CD交于点O.
(1)填空:∠BOC= 度;
(2)如图②,以CO为边作等边△OCF,AF与BO相等吗?并说明理由;
(3)如图③,若点G是BC的中点,连接AO、GO,判断AO与GO有什么数量关系?并说明理由.
(1)填空:∠BOC= 度;
(2)如图②,以CO为边作等边△OCF,AF与BO相等吗?并说明理由;
(3)如图③,若点G是BC的中点,连接AO、GO,判断AO与GO有什么数量关系?并说明理由.
您最近一年使用:0次
2021-07-15更新
|
2501次组卷
|
16卷引用:江西省抚州市2022-2023学年八年级下学期6月期末数学试题
江西省抚州市2022-2023学年八年级下学期6月期末数学试题广东省佛山市顺德区2020-2021学年七年级下学期期末数学试题江苏省泰州市靖江市实验学校2021-2022学年八年级上学期期中数学试题内蒙古锡林浩特市第一中学2021-2022学年八年级上学期期中考试数学试题湖南省长沙市望城区2020-2021学年八年级上学期期末数学试题(已下线)八年级上学期期中【压轴45题专练】-2022-2023学年八年级数学上学期考试满分全攻略(人教版)江苏省泰州市靖江市实验学校2022-2023学年八年级上学期10月月考数学试题新疆维吾尔自治区乌鲁木齐市沙依巴克区2022-2023学年八年级上学期期中数学试题(已下线)江苏八年级上学期期中【压轴35题考点专练】(前四章)-2022-2023学年八年级数学上学期考试满分全攻略(苏科版)湖南省常德市安乡县2022-2023学年八年级上学期期末数学质量监测卷2023年湖北省黄冈市教改联盟中考二模数学试卷2023年广东省广州市越秀区中考三模数学试题山东省济南市高新区2022-2023学年八年级下学期期中数学试题湖北省枣阳市2023-2024学年八年级上学期期末数学试题四川省眉山市东坡区万胜初级中学2023-2024学年八年级上学期期中数学试题河南省驻马店市第四中学2023-2024学年八年级下学期4月期中考试数学试题