1 . 某区高二年级4000名学生的期中检测的数学成绩服从正态分布 ,则成绩位于
,则成绩位于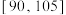 的人数大约是
的人数大约是_________________ .
(参考数据: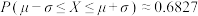 ,
,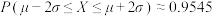 )
)
 ,则成绩位于
,则成绩位于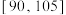 的人数大约是
的人数大约是(参考数据:
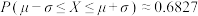 ,
,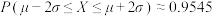 )
)
您最近一年使用:0次
2 . 某校进行的“校园安全”知识竞赛成绩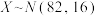 ,若成绩在90分以上为“优秀”,该校有4000人参加竞赛,则获得“优秀”的人数为
,若成绩在90分以上为“优秀”,该校有4000人参加竞赛,则获得“优秀”的人数为_________ .(附: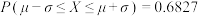 ,
,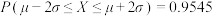 )
)
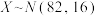 ,若成绩在90分以上为“优秀”,该校有4000人参加竞赛,则获得“优秀”的人数为
,若成绩在90分以上为“优秀”,该校有4000人参加竞赛,则获得“优秀”的人数为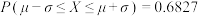 ,
,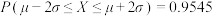 )
)
您最近一年使用:0次
3 . 在“飞彩镌流年”文艺汇演中,诸位参赛者一展风采,奉上了一场舞与乐的盛宴.现从2000位参赛者中随机抽取40位幸运嘉宾,统计他们的年龄数据,得样本平均数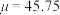 .
.
(1)若所有参赛者年龄 服从正态分布
服从正态分布 ,请估计参赛者年龄在30岁以上的人数(计算结果四舍五入取整数);
,请估计参赛者年龄在30岁以上的人数(计算结果四舍五入取整数);
(2)若该文艺汇演对所有参赛者的表演作品进行评级,每位参赛者只有一个表演作品且每位参赛者作品有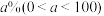 的概率评为
的概率评为 类,
类,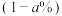 的概率评为
的概率评为 类,每位参赛者作品的评级结果相互独立.记上述40位幸运嘉宾的作品中恰有2份
类,每位参赛者作品的评级结果相互独立.记上述40位幸运嘉宾的作品中恰有2份 类作品的概率为
类作品的概率为 ,求
,求 的极大值点
的极大值点 ;
;
(3)以(2)中确定的 作为
作为 的值,记上述幸运嘉宾的作品中的
的值,记上述幸运嘉宾的作品中的 类作品数为
类作品数为 ,若对这些幸运嘉宾进行颁奖,现有两种颁奖方式:甲:
,若对这些幸运嘉宾进行颁奖,现有两种颁奖方式:甲: 类作品参赛者获得1000元现金,
类作品参赛者获得1000元现金, 类作品参赛者获得100元现金;乙:
类作品参赛者获得100元现金;乙: 类作品参赛者获得3000元现金,
类作品参赛者获得3000元现金, 类作品参赛者不获得现金奖励.根据奖金期望判断主办方选择何种颁奖方式,成本可能更低.
类作品参赛者不获得现金奖励.根据奖金期望判断主办方选择何种颁奖方式,成本可能更低.
附:若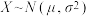 ,则
,则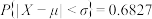 ,
,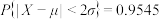 ,
,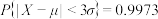 .
.
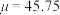 .
.(1)若所有参赛者年龄
 服从正态分布
服从正态分布 ,请估计参赛者年龄在30岁以上的人数(计算结果四舍五入取整数);
,请估计参赛者年龄在30岁以上的人数(计算结果四舍五入取整数);(2)若该文艺汇演对所有参赛者的表演作品进行评级,每位参赛者只有一个表演作品且每位参赛者作品有
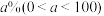 的概率评为
的概率评为 类,
类,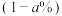 的概率评为
的概率评为 类,每位参赛者作品的评级结果相互独立.记上述40位幸运嘉宾的作品中恰有2份
类,每位参赛者作品的评级结果相互独立.记上述40位幸运嘉宾的作品中恰有2份 类作品的概率为
类作品的概率为 ,求
,求 的极大值点
的极大值点 ;
;(3)以(2)中确定的
 作为
作为 的值,记上述幸运嘉宾的作品中的
的值,记上述幸运嘉宾的作品中的 类作品数为
类作品数为 ,若对这些幸运嘉宾进行颁奖,现有两种颁奖方式:甲:
,若对这些幸运嘉宾进行颁奖,现有两种颁奖方式:甲: 类作品参赛者获得1000元现金,
类作品参赛者获得1000元现金, 类作品参赛者获得100元现金;乙:
类作品参赛者获得100元现金;乙: 类作品参赛者获得3000元现金,
类作品参赛者获得3000元现金, 类作品参赛者不获得现金奖励.根据奖金期望判断主办方选择何种颁奖方式,成本可能更低.
类作品参赛者不获得现金奖励.根据奖金期望判断主办方选择何种颁奖方式,成本可能更低.附:若
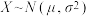 ,则
,则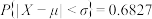 ,
,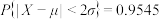 ,
,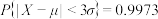 .
.
您最近一年使用:0次
名校
4 . 某次数学联考成绩的数据分析,20000名考生成绩服从正态分布 ,则80分以上的人数大约是( )
,则80分以上的人数大约是( )
 ,则80分以上的人数大约是( )
,则80分以上的人数大约是( )| A.3173 | B.6346 | C.6827 | D.13654 |
您最近一年使用:0次
5 . 书籍是精神世界的入口,阅读让精神世界闪光,阅读逐渐成为许多人的一种生活习惯,每年4月23日为世界读书日.某市某中学为了了解高一年级学生的阅读情况,从高一年级全部1000名学生中随机抽取100名学生,调查他们每周的阅读时间(单位:小时)并进行统计,得到样本的频率分布直方图如图所示. 服从正态分布
服从正态分布 ,其中
,其中 可以近似为100名学生的每周阅读时间的平均值(同组数据用该组数据区间的中点值表示),
可以近似为100名学生的每周阅读时间的平均值(同组数据用该组数据区间的中点值表示),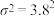 .
.
(1)试估计高一全体学生中每周阅读时间不高于6.8小时的人数(四舍五入取整);
(2)若从高一全体学生中随机抽取5名学生进行座谈,设选出的5人中每周阅读时间在10.6小时以上的学生人数为Y,求随机变量Y的分布列,数学期望与方差.
参考数据:若随机变量 服从正态分布
服从正态分布 ,则
,则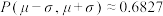 ,
,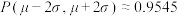 ,
,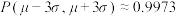 .
.
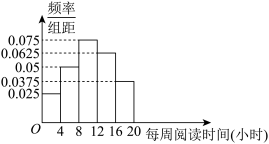
 服从正态分布
服从正态分布 ,其中
,其中 可以近似为100名学生的每周阅读时间的平均值(同组数据用该组数据区间的中点值表示),
可以近似为100名学生的每周阅读时间的平均值(同组数据用该组数据区间的中点值表示),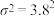 .
.(1)试估计高一全体学生中每周阅读时间不高于6.8小时的人数(四舍五入取整);
(2)若从高一全体学生中随机抽取5名学生进行座谈,设选出的5人中每周阅读时间在10.6小时以上的学生人数为Y,求随机变量Y的分布列,数学期望与方差.
参考数据:若随机变量
 服从正态分布
服从正态分布 ,则
,则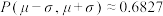 ,
,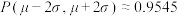 ,
,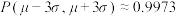 .
.
您最近一年使用:0次
名校
6 . 目前,教师职业越来越受青睐,考取教师资格证成为不少人的就业规划之一. 当前,中小学教师资格考试分笔试和面试两部分,笔试通过后才能进入面试环节. 已知某市2024年共有10000名考生参加了中小学教师资格考试的笔试,笔试成绩 ,只有笔试成绩高于70分的考生才能进入面试环节.
,只有笔试成绩高于70分的考生才能进入面试环节.
(1)利用正态分布的知识,估计该市报考中小学教师资格的10000名笔试考生中,进入面试的人数(结果只保留整数);
(2)现有甲、乙、丙3名考生进入了面试,且他们通过面试的概率分别为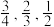 ,设这3名考生中通过面试的人数为
,设这3名考生中通过面试的人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
参考数据:若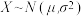 ,则
,则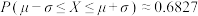 ,
,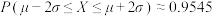 ,
,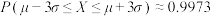 .
.
 ,只有笔试成绩高于70分的考生才能进入面试环节.
,只有笔试成绩高于70分的考生才能进入面试环节.(1)利用正态分布的知识,估计该市报考中小学教师资格的10000名笔试考生中,进入面试的人数(结果只保留整数);
(2)现有甲、乙、丙3名考生进入了面试,且他们通过面试的概率分别为
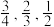 ,设这3名考生中通过面试的人数为
,设这3名考生中通过面试的人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.参考数据:若
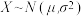 ,则
,则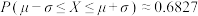 ,
,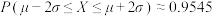 ,
,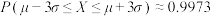 .
.
您最近一年使用:0次
7 . 某校体育锻炼时间准备提供三项体育活动供学生选择.为了解该校学生对“三项体育活动中要有篮球”这种观点的态度(态度分为同意和不同意),随机调查了200名学生,数据如下图:单位:人
(1)依据 的独立性检验,能否认为学生对“三项体育活动中要有篮球”这种观点的态度与性别有关?
的独立性检验,能否认为学生对“三项体育活动中要有篮球”这种观点的态度与性别有关?
(2)现有足球、篮球、跳绳供学生选择.
①若甲、乙两名学生从这三项运动中随机选一种,且他们的选择情况相互独立互不影响.记事件 为“甲学生选择足球”,事件
为“甲学生选择足球”,事件 为“甲、乙两名学生的选择不同”,判断事件
为“甲、乙两名学生的选择不同”,判断事件 是否独立,并说明理由.
是否独立,并说明理由.
②若该校所有学生每分钟跳绳个数 .根据往年经验,该校学生经过训练后,跳绳个数都有明显进步.假设经过训练后每人每分钟跳绳个数比开始时个数增加10,该校有1000名学生,预估经过训练后该校每分钟跳182个以上人数(结果四舍五入到整数).
.根据往年经验,该校学生经过训练后,跳绳个数都有明显进步.假设经过训练后每人每分钟跳绳个数比开始时个数增加10,该校有1000名学生,预估经过训练后该校每分钟跳182个以上人数(结果四舍五入到整数).
参考公式和数据: ,其中
,其中 .
.
若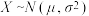 ,则
,则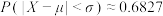 ,
,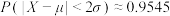 ,
, .
.
| 男生 | 女生 | 合计 | |
| 同意 | 70 | 50 | 120 |
| 不同意 | 30 | 50 | 80 |
| 合计 | 100 | 100 | 200 |
 的独立性检验,能否认为学生对“三项体育活动中要有篮球”这种观点的态度与性别有关?
的独立性检验,能否认为学生对“三项体育活动中要有篮球”这种观点的态度与性别有关?(2)现有足球、篮球、跳绳供学生选择.
①若甲、乙两名学生从这三项运动中随机选一种,且他们的选择情况相互独立互不影响.记事件
 为“甲学生选择足球”,事件
为“甲学生选择足球”,事件 为“甲、乙两名学生的选择不同”,判断事件
为“甲、乙两名学生的选择不同”,判断事件 是否独立,并说明理由.
是否独立,并说明理由.②若该校所有学生每分钟跳绳个数
 .根据往年经验,该校学生经过训练后,跳绳个数都有明显进步.假设经过训练后每人每分钟跳绳个数比开始时个数增加10,该校有1000名学生,预估经过训练后该校每分钟跳182个以上人数(结果四舍五入到整数).
.根据往年经验,该校学生经过训练后,跳绳个数都有明显进步.假设经过训练后每人每分钟跳绳个数比开始时个数增加10,该校有1000名学生,预估经过训练后该校每分钟跳182个以上人数(结果四舍五入到整数).参考公式和数据:
 ,其中
,其中 .
. | 0.025 | 0.010 | 0.005 |
 | 5.024 | 6.635 | 7.879 |
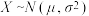 ,则
,则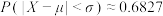 ,
,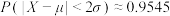 ,
, .
.
您最近一年使用:0次
24-25高二上·江苏·假期作业
8 . 某校拟对全校学生进行体能检测,并规定:学生体能检测成绩不低于60分为合格,否则为不合格;若全年级不合格人数不超过总人数的 ,则该年级体能检测达标,否则该年级体能检测不达标,需加强锻炼.
,则该年级体能检测达标,否则该年级体能检测不达标,需加强锻炼.
(1)为准备体能检测,甲、乙两位同学计划每天开展一轮羽毛球比赛以提高体能,并约定每轮比赛均采用七局四胜制(一方获胜四局则本轮比赛结束).假设甲同学每局比赛获胜的概率均为 ,求甲在一轮比赛中至少打了五局并获胜的条件下,前3局比赛均获胜的概率;
,求甲在一轮比赛中至少打了五局并获胜的条件下,前3局比赛均获胜的概率;
(2)经过一段时间的体能训练后,该校进行了体能检测,并从高二年级1000名学生中随机抽取了40名学生的成绩作分析.将这40名学生体能检测的平均成绩记为 ,标准差记为
,标准差记为 ,高二年级学生体能检测成绩近似服从正态分布
,高二年级学生体能检测成绩近似服从正态分布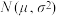 .已知
.已知 ,
, ,请估计该校高二年级学生体能检测是否合格?
,请估计该校高二年级学生体能检测是否合格?
附:若随机变量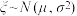 ,则
,则 ,
, ,
,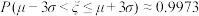 .
.
 ,则该年级体能检测达标,否则该年级体能检测不达标,需加强锻炼.
,则该年级体能检测达标,否则该年级体能检测不达标,需加强锻炼.(1)为准备体能检测,甲、乙两位同学计划每天开展一轮羽毛球比赛以提高体能,并约定每轮比赛均采用七局四胜制(一方获胜四局则本轮比赛结束).假设甲同学每局比赛获胜的概率均为
 ,求甲在一轮比赛中至少打了五局并获胜的条件下,前3局比赛均获胜的概率;
,求甲在一轮比赛中至少打了五局并获胜的条件下,前3局比赛均获胜的概率;(2)经过一段时间的体能训练后,该校进行了体能检测,并从高二年级1000名学生中随机抽取了40名学生的成绩作分析.将这40名学生体能检测的平均成绩记为
 ,标准差记为
,标准差记为 ,高二年级学生体能检测成绩近似服从正态分布
,高二年级学生体能检测成绩近似服从正态分布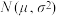 .已知
.已知 ,
, ,请估计该校高二年级学生体能检测是否合格?
,请估计该校高二年级学生体能检测是否合格?附:若随机变量
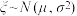 ,则
,则 ,
, ,
,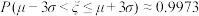 .
.
您最近一年使用:0次
名校
9 . 据统计,某外卖公司在 市的3000名外卖员每人的月成交单数
市的3000名外卖员每人的月成交单数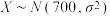 ,其中有600人的月成交单数超1100单,则该市外卖员月成交单数在区间
,其中有600人的月成交单数超1100单,则该市外卖员月成交单数在区间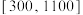 内的人数约为
内的人数约为__________ .
 市的3000名外卖员每人的月成交单数
市的3000名外卖员每人的月成交单数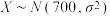 ,其中有600人的月成交单数超1100单,则该市外卖员月成交单数在区间
,其中有600人的月成交单数超1100单,则该市外卖员月成交单数在区间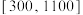 内的人数约为
内的人数约为
您最近一年使用:0次
名校
10 . 某校高二年级下学期期中考试数学试卷满分为150分,90分以上(含90分)为及格.阅卷结果显示,全年级800名学生的数学成绩近似服从正态分布,试卷的难度系数( 平均分/150)为
平均分/150)为 ,标准差为
,标准差为 ,则该次数学考试及格的人数约为( )
,则该次数学考试及格的人数约为( )
附:若 ,记
,记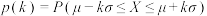 ,则
,则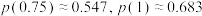 .
.
 平均分/150)为
平均分/150)为 ,标准差为
,标准差为 ,则该次数学考试及格的人数约为( )
,则该次数学考试及格的人数约为( )附:若
 ,记
,记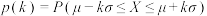 ,则
,则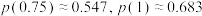 .
.| A.127人 | B.181人 | C.254人 | D.362人 |
您最近一年使用:0次



