名校
1 . 已知函数 ,
,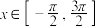 有以下结论:
有以下结论:
① 的图象关于直线
的图象关于直线 轴对称②
轴对称② 在区间
在区间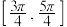 上单调递减
上单调递减
③ 的一个对称中心是
的一个对称中心是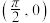 ④
④ 的最大值为
的最大值为
则上述说法正确的序号为__________ (请填上所有正确序号).
 ,
,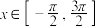 有以下结论:
有以下结论:①
 的图象关于直线
的图象关于直线 轴对称②
轴对称② 在区间
在区间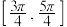 上单调递减
上单调递减③
 的一个对称中心是
的一个对称中心是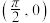 ④
④ 的最大值为
的最大值为
则上述说法正确的序号为
您最近一年使用:0次
2019-07-29更新
|
5758次组卷
|
15卷引用:辽宁省凌源二中2018-2019学年高一下学期期末数学试题
辽宁省凌源二中2018-2019学年高一下学期期末数学试题山东省菏泽市2018-2019学年高一下学期期末数学试题海南省海口市第一中学2019-2020学年高三上学期10月月考数学试题河北省石家庄市辛集市中学2019-2020学年高三第三次月考数学(文)试题山东省菏泽市东明县第一中学2018-2019学年高一下学期期末数学试题2020届海南省儋州市第一中学高三上学期第二次月考数学试题2020届福建省莆田第二十五中学高三上学期期末数学(文)试题(已下线)专题03 三角(第二篇)-备战2020高考数学黄金30题系列之压轴题(新课标版)山西省山西大学附属中学2019-2020学年高一下学期5月模块诊断数学试题黑龙江省哈尔滨市第六中学校2020-2021学年高三9月月考数学(文)试题黑龙江省哈尔滨市第六中学2020-2021学年度高三上学期九月月考文科数学试题(已下线)河南省三门峡市2020-2021学年度高三第一次大练习数学(理科)试题(已下线)5.6 函数y=Asin(ωx+φ) -2021-2022学年高一数学同步辅导讲义与检测(人教A版2019必修第一册)上海市奉贤区致远高级中学2021-2022学年高一下学期期中在线教学评估数学试题黑龙江省双鸭山市第一中学2022-2023学年高三上学期开学考试数学试题
名校
2 . 下列说法中不正确 的序号为____________ .
①若函数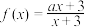 在
在 上单调递减,则实数
上单调递减,则实数 的取值范围是
的取值范围是 ;
;
②函数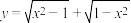 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③已知函数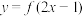 的定义域为
的定义域为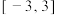 ,则函数
,则函数 的定义域是
的定义域是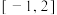 ;
;
④若函数 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
①若函数
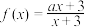 在
在 上单调递减,则实数
上单调递减,则实数 的取值范围是
的取值范围是 ;
;②函数
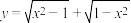 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;③已知函数
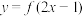 的定义域为
的定义域为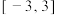 ,则函数
,则函数 的定义域是
的定义域是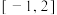 ;
; ④若函数
 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
您最近一年使用:0次
名校
3 . 关于函数 ,给出下列四个结论:①其图象关于点
,给出下列四个结论:①其图象关于点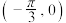 对称;②其图象关于直线
对称;②其图象关于直线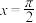 对称;③函数
对称;③函数 在
在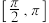 上的最大值为
上的最大值为 ;④其图象可由
;④其图象可由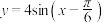 图象上所有的点横坐标变为原来的
图象上所有的点横坐标变为原来的 (纵坐标不变)得到.其中正确结论的序号为
(纵坐标不变)得到.其中正确结论的序号为______ .(把所有正确的结论序号都填上)
 ,给出下列四个结论:①其图象关于点
,给出下列四个结论:①其图象关于点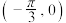 对称;②其图象关于直线
对称;②其图象关于直线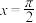 对称;③函数
对称;③函数 在
在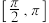 上的最大值为
上的最大值为 ;④其图象可由
;④其图象可由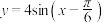 图象上所有的点横坐标变为原来的
图象上所有的点横坐标变为原来的 (纵坐标不变)得到.其中正确结论的序号为
(纵坐标不变)得到.其中正确结论的序号为
您最近一年使用:0次
名校
4 . 给出下列四个命题:
①函数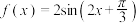 的一条对称轴是
的一条对称轴是 ;
;
②函数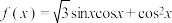 的图象关于点
的图象关于点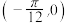 中心对称
中心对称
③ 中,
中, ,则
,则 为等腰三角形;
为等腰三角形;
④若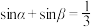 ,则
,则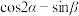 的最小值为
的最小值为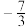 .
.
以上四个命题中正确命题的序号为_______ .(填出所有正确命题的序号)
①函数
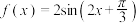 的一条对称轴是
的一条对称轴是 ;
;②函数
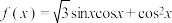 的图象关于点
的图象关于点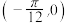 中心对称
中心对称③
 中,
中, ,则
,则 为等腰三角形;
为等腰三角形;④若
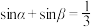 ,则
,则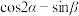 的最小值为
的最小值为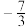 .
.以上四个命题中正确命题的序号为
您最近一年使用:0次
2019-09-26更新
|
503次组卷
|
2卷引用:安徽省六安市第一中学2019-2020学年高二上学期开学考试数学(理)试题
13-14高一上·海南省直辖县级单位·阶段练习
名校
解题方法
5 . 甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程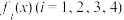 关于时间
关于时间 的函数关系式分别为
的函数关系式分别为 ,
,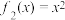 ,
,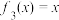 ,
,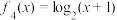 ,有以下结论:
,有以下结论:
①当 时,甲走在最前面;
时,甲走在最前面;
②当 时,乙走在最前面;
时,乙走在最前面;
③当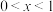 时,丁走在最前面,当
时,丁走在最前面,当 时,丁走在最后面;
时,丁走在最后面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为_________ (把正确结论的序号都填上,多填或少填均不得分).
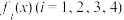 关于时间
关于时间 的函数关系式分别为
的函数关系式分别为 ,
,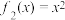 ,
,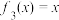 ,
,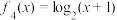 ,有以下结论:
,有以下结论:①当
 时,甲走在最前面;
时,甲走在最前面;②当
 时,乙走在最前面;
时,乙走在最前面;③当
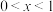 时,丁走在最前面,当
时,丁走在最前面,当 时,丁走在最后面;
时,丁走在最后面;④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为
您最近一年使用:0次
2017-11-27更新
|
914次组卷
|
14卷引用:贵州省遵义市南白中学2019-2020学年高一上学期第三次月考数学试题
贵州省遵义市南白中学2019-2020学年高一上学期第三次月考数学试题(已下线)2013-2014学年海南琼海市嘉积中学高一上学期段考数学试卷(已下线)2013-2014学年海南琼海嘉积中学高一上学期段考数学试卷2015-2016学年甘肃省兰州一中高一上学期期末数学试卷12015-2016学年河南省鹤壁市高一上学期期末数学试卷2015-2016学年甘肃省兰州一中高一上学期期末数学试卷2(已下线)同步君人教A版必修1第三章3.2.1 几类不同增长的函数模型2016-2017学年湖南长沙长郡中学高一上学期期中数学试卷贵州省铜仁市思南中学2017-2018学年高一上学期期中考试数学试题高中数学人教版 必修1 第三章 函数的应用 3.2.1 几类不同增长的函数模型人教B版(2019) 必修第二册 逆袭之路 第四章 4.6 函数的应用(二)8.2.1 几个函数模型的比较(练习)-2020-2021学年上学期高一数学同步精品课堂(新教材苏教版必修第一册)(35张PPT)2023版 湘教版(2019) 必修第一册 过关斩将 第4章 4.5.1几种函数增长快慢的比较4.5.1 几种函数增长快慢的比较 课时训练
12-13高二上·甘肃武威·阶段练习
6 . 已知命题p:存在x∈R,使tan x=1,命题q:x2-3x+2<0的解集是{x|1<x<2},现有以下结论:
①命题“p且q”是真命题;②命题“p且¬q”是假命题;③命题“¬p或q”是真命题;④命题“¬p或¬q”是假命题.
其中正确结论的序号为________ .(写出所有正确结论的序号)
①命题“p且q”是真命题;②命题“p且¬q”是假命题;③命题“¬p或q”是真命题;④命题“¬p或¬q”是假命题.
其中正确结论的序号为
您最近一年使用:0次
2016-12-03更新
|
1362次组卷
|
8卷引用:2019高考备考一轮复习精品资料 【文】专题三 简单的逻辑联结词 押题专练
(已下线)2019高考备考一轮复习精品资料 【文】专题三 简单的逻辑联结词 押题专练(已下线)2019高考热点题型和提分秘籍 【文数】专题3 逻辑联结词、全称量词与存在量词( 题型专练)(已下线)2012-2013学年甘肃武威六中高二12月学段检测理科数学试卷(已下线)2015高考数学一轮配套特训:1-3简单的逻辑联结词全称量词与存在量词(已下线)章末质量检测1 常用逻辑用语-2018年数学同步优化指导(北师大版选修2-1)(已下线)2019高考热点题型和提分秘籍 【理数】专题3 逻辑联结词、全称量词与存在量词 (题型专练)(已下线)专题1.3 简单的逻辑联结词、全称量词与存在量词(精测)-2021届高考数学(理)一轮复习讲练测河南省兰考县第二高级中学2021-2022学年高二上学期第三次考试数学试题
名校
7 . 给出下列三种说法:
①命题p:∃x0∈R,tan x0=1,命题q:∀x∈R,x2-x+1>0,则命题“p∧(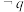 )”是假命题.
)”是假命题.
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是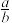 =-3.
=-3.
③命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”.
其中所有正确说法的序号为________________ .
①命题p:∃x0∈R,tan x0=1,命题q:∀x∈R,x2-x+1>0,则命题“p∧(
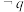 )”是假命题.
)”是假命题.②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是
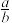 =-3.
=-3.③命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”.
其中所有正确说法的序号为
您最近一年使用:0次
2016-12-05更新
|
1025次组卷
|
6卷引用:辽宁省沈阳市郊联体2018-2019 学年高二上学期数学(文科)期末试题
辽宁省沈阳市郊联体2018-2019 学年高二上学期数学(文科)期末试题2016-2017学年河北馆陶县一中高二上期中数学试卷黑龙江省海林市朝鲜族中学高三数学人教版选修1-1同步练习:第一章 常用逻辑用语单元测评江西省会昌中学2018-2019学年高二上学期第一次月考数学(理)试卷(已下线)专题1.3 简单的逻辑联结词、全称量词与存在量词(精练)-2021年高考数学(文)一轮复习学与练广西壮族自治区钦州市第四中学2023届高三上学期9月考试数学(文)试题
名校
解题方法
8 . 已知函数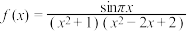 .
.
(1)那么方程 在区间
在区间 上的根的个数是
上的根的个数是___________ .
(2)对于下列命题:
①函数 是周期函数;
是周期函数;
②函数 既有最大值又有最小值;
既有最大值又有最小值;
③函数 的定义域是
的定义域是 ,且其图象有对称轴;
,且其图象有对称轴;
④在开区间 上,
上, 单调递减.
单调递减.
其中真命题的序号为______________ (填写真命题的序号).
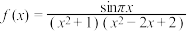 .
.(1)那么方程
 在区间
在区间 上的根的个数是
上的根的个数是(2)对于下列命题:
①函数
 是周期函数;
是周期函数;②函数
 既有最大值又有最小值;
既有最大值又有最小值;③函数
 的定义域是
的定义域是 ,且其图象有对称轴;
,且其图象有对称轴;④在开区间
 上,
上, 单调递减.
单调递减.其中真命题的序号为
您最近一年使用:0次
9 . 定义在 上的函数
上的函数 ,如果存在函数
,如果存在函数 (
( ,
, 为常数),使得
为常数),使得 对一切实数
对一切实数 都成立则称
都成立则称 为函数
为函数 的一个承托函数.现有如下函数:①
的一个承托函数.现有如下函数:①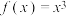 ;②
;②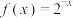 ;③
;③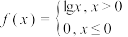 ;④
;④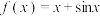 .则存在承托函数的
.则存在承托函数的 的序号为
的序号为______ .(填入满足题意的所有序号)
 上的函数
上的函数 ,如果存在函数
,如果存在函数 (
( ,
, 为常数),使得
为常数),使得 对一切实数
对一切实数 都成立则称
都成立则称 为函数
为函数 的一个承托函数.现有如下函数:①
的一个承托函数.现有如下函数:①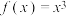 ;②
;②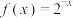 ;③
;③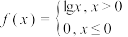 ;④
;④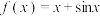 .则存在承托函数的
.则存在承托函数的 的序号为
的序号为
您最近一年使用:0次
解题方法
10 . 函数 的函数值表示不超过
的函数值表示不超过 的最大整数,例如,
的最大整数,例如, ,
,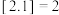 .则对于函数
.则对于函数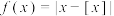 ,有下列说法:①
,有下列说法:① 的值域为
的值域为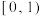 ;②
;② 是1为周期的周期函数;③
是1为周期的周期函数;③ 是偶函数;④
是偶函数;④ 在区间
在区间 上是单调递增函数.其中,正确的命题序号为
上是单调递增函数.其中,正确的命题序号为___________ .
 的函数值表示不超过
的函数值表示不超过 的最大整数,例如,
的最大整数,例如, ,
,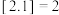 .则对于函数
.则对于函数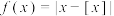 ,有下列说法:①
,有下列说法:① 的值域为
的值域为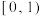 ;②
;② 是1为周期的周期函数;③
是1为周期的周期函数;③ 是偶函数;④
是偶函数;④ 在区间
在区间 上是单调递增函数.其中,正确的命题序号为
上是单调递增函数.其中,正确的命题序号为
您最近一年使用:0次



