1 . 在2023年杭州亚运会最后两个竞技项目男女马拉松比赛中,中国选手何杰以2小时13分02秒夺得男子组冠军,这是中国队亚运史上首枚男子马拉松金牌.人类长跑运动一般分为两个阶段,第一阶段为前1小时的稳定阶段,第二阶段为疲劳阶段.小明想通过数学建模的方式研究运动员的运动时长与其剩余体力的关系.通过查找资料,小明得知:一位60kg的复健马拉松运动员进行4小时长跑训练,稳定阶段平均速度为30km/h,该阶段每千克体重消耗体力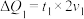 (
(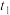 表示该阶段所用时间),疲劳阶段由于体力消耗过大,在原有基础上随时间变大,速度降低,比例系数为
表示该阶段所用时间),疲劳阶段由于体力消耗过大,在原有基础上随时间变大,速度降低,比例系数为 .同时,疲劳阶段速度降低,体力得到一定恢复,该阶段每千克体重消耗体力
.同时,疲劳阶段速度降低,体力得到一定恢复,该阶段每千克体重消耗体力 ,(
,(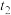 表示该阶段所用时间).同时,根据比赛现场的环境,其他运动员的平均配速,以及比赛策略等各方面因素,产生上下5%~10%的速度浮动,其对于运动员的体力影响也更为复杂.已知该运动员初始体力为
表示该阶段所用时间).同时,根据比赛现场的环境,其他运动员的平均配速,以及比赛策略等各方面因素,产生上下5%~10%的速度浮动,其对于运动员的体力影响也更为复杂.已知该运动员初始体力为 ,请帮助小明补充完善数学建模的过程:
,请帮助小明补充完善数学建模的过程:
(1)对于数学建模,我们需要给出合理假设.
假设一:假设该运动员稳定阶段作速度为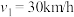 的匀速运动;疲劳阶段做
的匀速运动;疲劳阶段做 的减速运动
的减速运动
假设二:_________________
(2)提出问题一:该运动员剩余体力Q关于时间t有何关系?请写出函数 ;
;
提出问题二:该运动员在4小时内何时体力达到最低值,最低值为多少?
(3)总结运用:请根据以上计算结论,给出一定的实际建议.
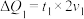 (
(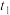 表示该阶段所用时间),疲劳阶段由于体力消耗过大,在原有基础上随时间变大,速度降低,比例系数为
表示该阶段所用时间),疲劳阶段由于体力消耗过大,在原有基础上随时间变大,速度降低,比例系数为 .同时,疲劳阶段速度降低,体力得到一定恢复,该阶段每千克体重消耗体力
.同时,疲劳阶段速度降低,体力得到一定恢复,该阶段每千克体重消耗体力 ,(
,(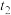 表示该阶段所用时间).同时,根据比赛现场的环境,其他运动员的平均配速,以及比赛策略等各方面因素,产生上下5%~10%的速度浮动,其对于运动员的体力影响也更为复杂.已知该运动员初始体力为
表示该阶段所用时间).同时,根据比赛现场的环境,其他运动员的平均配速,以及比赛策略等各方面因素,产生上下5%~10%的速度浮动,其对于运动员的体力影响也更为复杂.已知该运动员初始体力为 ,请帮助小明补充完善数学建模的过程:
,请帮助小明补充完善数学建模的过程:(1)对于数学建模,我们需要给出合理假设.
假设一:假设该运动员稳定阶段作速度为
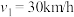 的匀速运动;疲劳阶段做
的匀速运动;疲劳阶段做 的减速运动
的减速运动假设二:_________________
(2)提出问题一:该运动员剩余体力Q关于时间t有何关系?请写出函数
 ;
;提出问题二:该运动员在4小时内何时体力达到最低值,最低值为多少?
(3)总结运用:请根据以上计算结论,给出一定的实际建议.
您最近一年使用:0次
名校
2 . 如果对于函数 的定义域内任意的
的定义域内任意的 ,都有
,都有 成立,那么就称函数
成立,那么就称函数 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数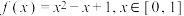 是否是“平缓函数”;
是否是“平缓函数”;
(2)若函数 是闭区间
是闭区间 上的“平缓函数”,且
上的“平缓函数”,且 ,证明:对于任意的
,证明:对于任意的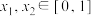 ,都有
,都有 成立.
成立.
 的定义域内任意的
的定义域内任意的 ,都有
,都有 成立,那么就称函数
成立,那么就称函数 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.(1)判断函数
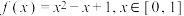 是否是“平缓函数”;
是否是“平缓函数”;(2)若函数
 是闭区间
是闭区间 上的“平缓函数”,且
上的“平缓函数”,且 ,证明:对于任意的
,证明:对于任意的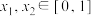 ,都有
,都有 成立.
成立.
您最近一年使用:0次
名校
3 . 已知 是定义在
是定义在 上的偶函数,当
上的偶函数,当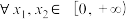 ,且
,且 时,
时,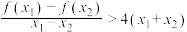 恒成立,
恒成立,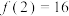 ,则满足
,则满足 的
的 的取值范围为
的取值范围为______ .
 是定义在
是定义在 上的偶函数,当
上的偶函数,当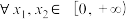 ,且
,且 时,
时,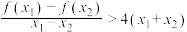 恒成立,
恒成立,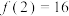 ,则满足
,则满足 的
的 的取值范围为
的取值范围为
您最近一年使用:0次
名校
解题方法
4 . 已知函数 ,
, 满足以下条件:
满足以下条件:
①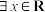 ,
,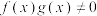 ;
;
②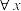 ,
,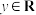 ,
,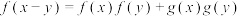 ,
,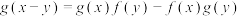 .
.
(1)求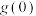 ,
,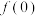 的值.
的值.
(2)判断函数 ,
, 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(3)若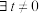 ,
,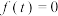 ,试判断函数
,试判断函数 的周期性,并说明理由.
的周期性,并说明理由.
 ,
, 满足以下条件:
满足以下条件:①
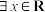 ,
,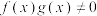 ;
;②
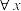 ,
,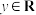 ,
,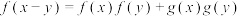 ,
,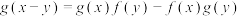 .
.(1)求
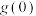 ,
,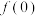 的值.
的值.(2)判断函数
 ,
, 的奇偶性,并说明理由.
的奇偶性,并说明理由.(3)若
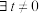 ,
,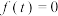 ,试判断函数
,试判断函数 的周期性,并说明理由.
的周期性,并说明理由.
您最近一年使用:0次
名校
解题方法
5 . 已知函数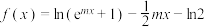 .
.
(1)若函数 为奇函数,求实数
为奇函数,求实数 的值;
的值;
(2)求函数 的值域;
的值域;
(3)求函数 的单调区间;
的单调区间;
(4)若关于 的不等式
的不等式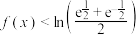 的解集
的解集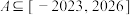 ,求实数
,求实数 的取值范围.
的取值范围.
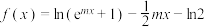 .
.(1)若函数
 为奇函数,求实数
为奇函数,求实数 的值;
的值;(2)求函数
 的值域;
的值域;(3)求函数
 的单调区间;
的单调区间;(4)若关于
 的不等式
的不等式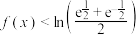 的解集
的解集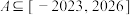 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
6 . 定义 为不超过
为不超过 的最大整数,如
的最大整数,如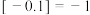 ,
,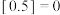 ,
, ,
, .已知函数
.已知函数 满足:对任意
满足:对任意 .
.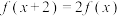 .当
.当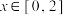 时,
时, ,则函数
,则函数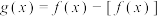 在
在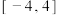 上的零点个数为( )
上的零点个数为( )
 为不超过
为不超过 的最大整数,如
的最大整数,如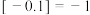 ,
,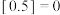 ,
, ,
, .已知函数
.已知函数 满足:对任意
满足:对任意 .
.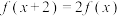 .当
.当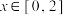 时,
时, ,则函数
,则函数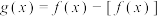 在
在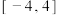 上的零点个数为( )
上的零点个数为( )| A.6 | B.8 | C.9 | D.10 |
您最近一年使用:0次
7日内更新
|
166次组卷
|
2卷引用:云南省部分校2023-2024学年高一下学期月考联考数学试题
名校
解题方法
7 . 设集合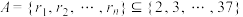 ,(
,( ,
, )且A中任意两数之和不能被5整除,则n的最大值为
)且A中任意两数之和不能被5整除,则n的最大值为____________ .
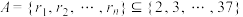 ,(
,( ,
, )且A中任意两数之和不能被5整除,则n的最大值为
)且A中任意两数之和不能被5整除,则n的最大值为
您最近一年使用:0次
名校
8 . 已知 为实数集的一个非空子集,称
为实数集的一个非空子集,称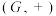 是一个加法群,如果
是一个加法群,如果 连同其上的加法运算满足如下四条性质:
连同其上的加法运算满足如下四条性质:
①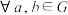 ,
, ;
;
② ,
, ;
;
③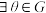 ,
,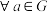 ,使得
,使得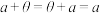 ;
;
④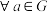 ,
, ,使得
,使得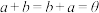 .
.
例如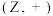 是一个无限元加法群,
是一个无限元加法群, 是一个单元素加法群.
是一个单元素加法群.
(1)令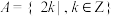 ,
,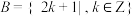 ,分别判断
,分别判断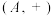 ,
,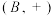 是否为加法群,并说明理由;
是否为加法群,并说明理由;
(2)已知非空集合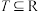 ,并且
,并且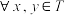 ,有
,有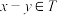 ,求证:
,求证: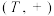 是一个加法群;
是一个加法群;
(3)已知非空集合 ,并且
,并且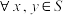 ,有
,有 ,求证:存在
,求证:存在 ,使得
,使得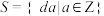 .
.
 为实数集的一个非空子集,称
为实数集的一个非空子集,称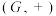 是一个加法群,如果
是一个加法群,如果 连同其上的加法运算满足如下四条性质:
连同其上的加法运算满足如下四条性质:①
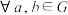 ,
, ;
;②
 ,
, ;
;③
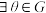 ,
,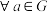 ,使得
,使得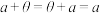 ;
;④
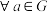 ,
, ,使得
,使得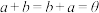 .
.例如
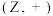 是一个无限元加法群,
是一个无限元加法群, 是一个单元素加法群.
是一个单元素加法群.(1)令
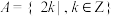 ,
,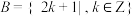 ,分别判断
,分别判断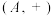 ,
,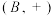 是否为加法群,并说明理由;
是否为加法群,并说明理由;(2)已知非空集合
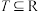 ,并且
,并且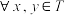 ,有
,有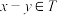 ,求证:
,求证: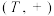 是一个加法群;
是一个加法群;(3)已知非空集合
 ,并且
,并且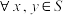 ,有
,有 ,求证:存在
,求证:存在 ,使得
,使得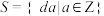 .
.
您最近一年使用:0次
名校
9 . 定义1:对于一个数集 ,定义一种运算
,定义一种运算 ,对任意
,对任意 都有
都有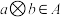 ,则称集合
,则称集合 关于运算
关于运算 是封闭的(例如:自然数集
是封闭的(例如:自然数集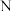 对于加法运算是封闭的).
对于加法运算是封闭的).
定义2:对于一个数集 ,若存在一个元素
,若存在一个元素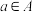 ,使得任意
,使得任意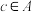 ,满足
,满足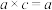 ,则称
,则称 为集合
为集合 中的零元,若存在一个元素
中的零元,若存在一个元素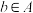 ,使得任意
,使得任意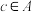 ,满足
,满足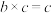 ,则称
,则称 为集合
为集合 中的单位元(例如:0和1分别为自然数集
中的单位元(例如:0和1分别为自然数集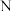 中的零元和单位元).
中的零元和单位元).
定义3:对于一个数集 ,如果满足下列关系:
,如果满足下列关系:
①有零元和单位元;
②关于加、减、乘、除(除数不为0)四种运算都是封闭的;
③对于乘法和加法都满足交换律和结合律,且满足乘法对加法的分配律,则称这个数集 是一个数域.
是一个数域.
(1)指出常用数集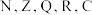 中,那些数集可以构成数域(不需要证明);
中,那些数集可以构成数域(不需要证明);
(2)已知集合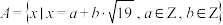 ,证明:集合
,证明:集合 关于乘法运算是封闭的;
关于乘法运算是封闭的;
(3)已知集合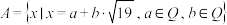 ,证明:集合
,证明:集合 是一个数域.
是一个数域.
 ,定义一种运算
,定义一种运算 ,对任意
,对任意 都有
都有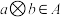 ,则称集合
,则称集合 关于运算
关于运算 是封闭的(例如:自然数集
是封闭的(例如:自然数集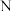 对于加法运算是封闭的).
对于加法运算是封闭的).定义2:对于一个数集
 ,若存在一个元素
,若存在一个元素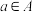 ,使得任意
,使得任意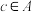 ,满足
,满足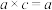 ,则称
,则称 为集合
为集合 中的零元,若存在一个元素
中的零元,若存在一个元素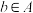 ,使得任意
,使得任意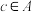 ,满足
,满足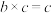 ,则称
,则称 为集合
为集合 中的单位元(例如:0和1分别为自然数集
中的单位元(例如:0和1分别为自然数集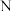 中的零元和单位元).
中的零元和单位元).定义3:对于一个数集
 ,如果满足下列关系:
,如果满足下列关系:①有零元和单位元;
②关于加、减、乘、除(除数不为0)四种运算都是封闭的;
③对于乘法和加法都满足交换律和结合律,且满足乘法对加法的分配律,则称这个数集
 是一个数域.
是一个数域. (1)指出常用数集
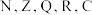 中,那些数集可以构成数域(不需要证明);
中,那些数集可以构成数域(不需要证明);(2)已知集合
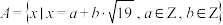 ,证明:集合
,证明:集合 关于乘法运算是封闭的;
关于乘法运算是封闭的;(3)已知集合
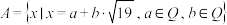 ,证明:集合
,证明:集合 是一个数域.
是一个数域.
您最近一年使用:0次
名校
解题方法
10 . 设 ,若非空集合
,若非空集合 同时满足以下4个条件,则称
同时满足以下4个条件,则称 是“
是“ 无和划分”:
无和划分”:
①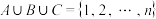 ;
;
②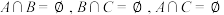 ;
;
③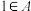 ,且
,且 中的最小元素大于
中的最小元素大于 中的最小元素;
中的最小元素;
④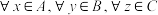 ,必有
,必有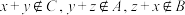 .
.
(1)若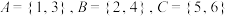 ,判断
,判断 是否是“
是否是“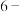 无和划分”,并说明理由.
无和划分”,并说明理由.
(2)已知 是“
是“ 无和划分”(
无和划分”( ).
).
①证明:对于任意 ,都有
,都有 ;
;
②若存在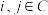 ,使得
,使得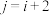 ,记
,记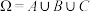 ,证明:
,证明: 中的所有奇数都属于
中的所有奇数都属于 .
.
 ,若非空集合
,若非空集合 同时满足以下4个条件,则称
同时满足以下4个条件,则称 是“
是“ 无和划分”:
无和划分”:①
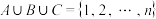 ;
;②
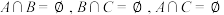 ;
;③
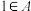 ,且
,且 中的最小元素大于
中的最小元素大于 中的最小元素;
中的最小元素;④
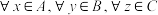 ,必有
,必有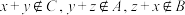 .
.(1)若
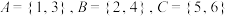 ,判断
,判断 是否是“
是否是“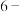 无和划分”,并说明理由.
无和划分”,并说明理由.(2)已知
 是“
是“ 无和划分”(
无和划分”( ).
).①证明:对于任意
 ,都有
,都有 ;
;②若存在
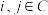 ,使得
,使得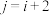 ,记
,记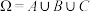 ,证明:
,证明: 中的所有奇数都属于
中的所有奇数都属于 .
.
您最近一年使用:0次
2024-06-10更新
|
131次组卷
|
2卷引用:北京市丰台区2023-2024学年高一上学期期末练习数学试卷



