1 . 已知 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
 ,则“
,则“ ”是“
”是“ ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
解题方法
2 . 已知 ,直线
,直线 :
: ,
, :
: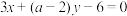 ,则“
,则“ ”是“
”是“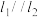 ”的( )
”的( )
 ,直线
,直线 :
: ,
, :
: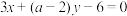 ,则“
,则“ ”是“
”是“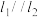 ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
3 .  是函数
是函数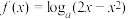 在
在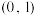 上单调递增的( )
上单调递增的( )
 是函数
是函数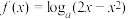 在
在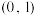 上单调递增的( )
上单调递增的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
名校
解题方法
4 . 已知全集 ,集合
,集合 ,则“
,则“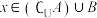 ”是“
”是“ ”的( )
”的( )
 ,集合
,集合 ,则“
,则“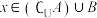 ”是“
”是“ ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
2024-02-03更新
|
828次组卷
|
3卷引用:安徽省合肥市第六中学2023-2024学年高一上学期12月月考数学试题
名校
解题方法
5 . 已知正实数a,b,设甲: ;乙:
;乙: ,则甲是乙的( )
,则甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
2024-01-31更新
|
197次组卷
|
4卷引用:安徽省阜阳市2023-2024学年高一上学期期末联考数学试卷
名校
解题方法
6 . 记 是数列
是数列 的前
的前 项和,设甲:
项和,设甲: 为等差数列;设乙:
为等差数列;设乙: ,则( )
,则( )
 是数列
是数列 的前
的前 项和,设甲:
项和,设甲: 为等差数列;设乙:
为等差数列;设乙: ,则( )
,则( )| A.甲是乙的充分条件但不是必要条件 |
| B.甲是乙的必要条件但不是充分条件 |
| C.甲是乙的充要条件 |
| D.甲既不是乙的充分条件也不是乙的必要条件 |
您最近半年使用:0次
2024-01-31更新
|
1238次组卷
|
5卷引用:浙江省湖州市2024届高三上学期期末数学试题
浙江省湖州市2024届高三上学期期末数学试题2024年普通高等学校招生全国统一考试数学模拟试题(一)(新高考九省联考题型)(已下线)最新模拟复盘卷1 模块一 各地期末考试精选汇编(已下线)考点4 条件的判断 --2024届高考数学考点总动员【练】黑龙江省牡丹江市第一高级中学2023-2024学年高二下学期开学考试数学试题
名校
解题方法
7 . “ 且
且 ”是“
”是“ 为第四象限角”的( )
为第四象限角”的( )
 且
且 ”是“
”是“ 为第四象限角”的( )
为第四象限角”的( )| A.充要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
2024-01-29更新
|
349次组卷
|
2卷引用:广东省深圳市龙岗区2023-2024学年高一上学期1月期末质量监测数学试题
名校
8 . 设函数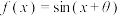 ,则“
,则“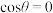 ”是“
”是“ 为偶函数”的( )
为偶函数”的( )
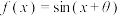 ,则“
,则“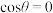 ”是“
”是“ 为偶函数”的( )
为偶函数”的( )| A.充分而不必要条件 | B.必要而不充分条件 | C.充分必要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
2024-01-29更新
|
284次组卷
|
2卷引用:浙江省杭州第二中学2023-2024学年高一上学期期末数学试题
解题方法
9 . 记 为数列
为数列 的前n项和,以下命题是真命题的是( )
的前n项和,以下命题是真命题的是( )
 为数列
为数列 的前n项和,以下命题是真命题的是( )
的前n项和,以下命题是真命题的是( )A. 是等差数列,则 是等差数列,则 的充要条件为 的充要条件为 |
B. 是等比数列,则 是等比数列,则 的充要条件为 的充要条件为 |
C. 是等差数列的充要条件为 是等差数列的充要条件为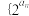 ﹜是等比数列 ﹜是等比数列 |
D. 是等差数列的充要条件为 是等差数列的充要条件为 为等差数列 为等差数列 |
您最近半年使用:0次
10 . “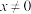 且
且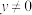 ”是“
”是“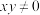 ”的( )
”的( )
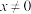 且
且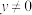 ”是“
”是“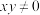 ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次



