名校
解题方法
1 . 微分中值定理是微积分学中的重要定理,它是研究区间上函数值变化规律的有效工具,其中拉格朗日中值定理是核心,它的内容如下:
如果函数 在闭区间
在闭区间 上连续,在开区间
上连续,在开区间 可导,导数为
可导,导数为 ,那么在开区间
,那么在开区间 内至少存在一点
内至少存在一点 ,使得
,使得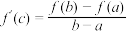 ,其中
,其中 叫做
叫做 在
在 上的“拉格朗日中值点”.已知函数
上的“拉格朗日中值点”.已知函数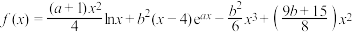 .
.
(1)若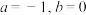 ,求函数
,求函数 在
在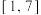 上的“拉格朗日中值点”
上的“拉格朗日中值点” ;
;
(2)若 ,求证:函数
,求证:函数 在区间
在区间 图象上任意两点
图象上任意两点 ,
, 连线的斜率不大于
连线的斜率不大于 ;
;
(3)若 ,且
,且 ,求证:
,求证: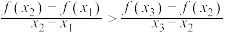 .
.
如果函数
 在闭区间
在闭区间 上连续,在开区间
上连续,在开区间 可导,导数为
可导,导数为 ,那么在开区间
,那么在开区间 内至少存在一点
内至少存在一点 ,使得
,使得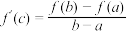 ,其中
,其中 叫做
叫做 在
在 上的“拉格朗日中值点”.已知函数
上的“拉格朗日中值点”.已知函数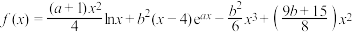 .
.(1)若
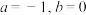 ,求函数
,求函数 在
在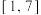 上的“拉格朗日中值点”
上的“拉格朗日中值点” ;
;(2)若
 ,求证:函数
,求证:函数 在区间
在区间 图象上任意两点
图象上任意两点 ,
, 连线的斜率不大于
连线的斜率不大于 ;
;(3)若
 ,且
,且 ,求证:
,求证: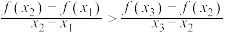 .
.
您最近一年使用:0次
2024-05-28更新
|
537次组卷
|
4卷引用:江西省上饶市横峰中学2023-2024学年高二下学期期末考试数学试卷
江西省上饶市横峰中学2023-2024学年高二下学期期末考试数学试卷湖南省常德市第一中学2023-2024学年高二下学期期末考试数学试卷2024届山西省高考三模数学试题(已下线)专题2 函数与导数新定义压轴大题(三)【讲】
名校
解题方法
2 . 拟合(Fittiong)和插值(Imorterpolation)都是利用已知的离散数据点来构造一个能够反映数据变化规律的近似函数,并以此预测或估计未知数据的方法.拟合方法在整体上寻求最好地逼近数据,适用于给定数据可能包含误差的情况,比如线性回归就是一种拟合方法;而插值方法要求近似函数经过所有的已知数据点.适用于需要高精度模型的场景,实际应用中常用多项式函数来逼近原函数,我们称之为移项式插值.例如,为了得到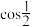 的近似值,我们对函数
的近似值,我们对函数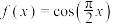 进行多项式插值.设一次函数
进行多项式插值.设一次函数 满足
满足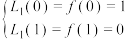 ,可得
,可得 在
在 上的一次插值多项式
上的一次插值多项式 ,由此可计算出
,由此可计算出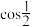 的“近似值”
的“近似值”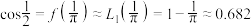 ,显然这个“近似值”与真实值的误差较大.为了减小插值估计的误差,除了要求插值函数与原函数在给定节点处的函数值相等,还可要求在部分节点处的导数值也相等,甚至要求高阶导数也相等.满足这种要求的插值多项式称为埃尔米特(Hermite)插值多项式.已知函数
,显然这个“近似值”与真实值的误差较大.为了减小插值估计的误差,除了要求插值函数与原函数在给定节点处的函数值相等,还可要求在部分节点处的导数值也相等,甚至要求高阶导数也相等.满足这种要求的插值多项式称为埃尔米特(Hermite)插值多项式.已知函数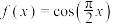 在
在 上的二次埃尔米特插值多项式
上的二次埃尔米特插值多项式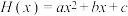 满足
满足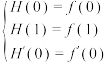
(1)求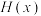 ,并证明当
,并证明当 时,
时, ;
;
(2)若当 时,
时,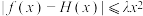 ,求实数
,求实数 的取值范围;
的取值范围;
(3)利用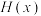 计算
计算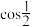 的近似值,并证明其误差不超过
的近似值,并证明其误差不超过 .
.
(参考数据: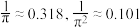 ;结果精确到0.001)
;结果精确到0.001)
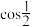 的近似值,我们对函数
的近似值,我们对函数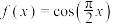 进行多项式插值.设一次函数
进行多项式插值.设一次函数 满足
满足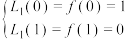 ,可得
,可得 在
在 上的一次插值多项式
上的一次插值多项式 ,由此可计算出
,由此可计算出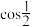 的“近似值”
的“近似值”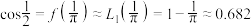 ,显然这个“近似值”与真实值的误差较大.为了减小插值估计的误差,除了要求插值函数与原函数在给定节点处的函数值相等,还可要求在部分节点处的导数值也相等,甚至要求高阶导数也相等.满足这种要求的插值多项式称为埃尔米特(Hermite)插值多项式.已知函数
,显然这个“近似值”与真实值的误差较大.为了减小插值估计的误差,除了要求插值函数与原函数在给定节点处的函数值相等,还可要求在部分节点处的导数值也相等,甚至要求高阶导数也相等.满足这种要求的插值多项式称为埃尔米特(Hermite)插值多项式.已知函数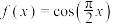 在
在 上的二次埃尔米特插值多项式
上的二次埃尔米特插值多项式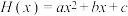 满足
满足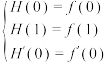
(1)求
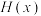 ,并证明当
,并证明当 时,
时, ;
;(2)若当
 时,
时,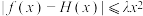 ,求实数
,求实数 的取值范围;
的取值范围;(3)利用
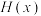 计算
计算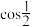 的近似值,并证明其误差不超过
的近似值,并证明其误差不超过 .
.(参考数据:
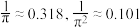 ;结果精确到0.001)
;结果精确到0.001)
您最近一年使用:0次
3 . 牛顿(1643-1727)给出了牛顿切线法求方程的近似解:如图设 是
是 的一个零点,任意选取
的一个零点,任意选取 作为
作为 的初始近似值,过点
的初始近似值,过点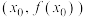 作曲线
作曲线 的切线
的切线 ,
, 与
与 轴的交点为横坐标为
轴的交点为横坐标为 ,称
,称 为
为 的1次近似值,过点
的1次近似值,过点 作曲线
作曲线 的切线
的切线 ,
, 与
与 轴的交点为横坐标为
轴的交点为横坐标为 ,称
,称 为
为 的2次近似值.一般地,过点
的2次近似值.一般地,过点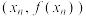 作曲线
作曲线 的切线
的切线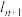 ,
,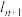 与
与 轴的交点为横坐标为
轴的交点为横坐标为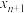 ,就称
,就称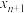 为
为 的
的 次近似值,称数列
次近似值,称数列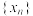 为牛顿数列.
为牛顿数列.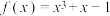 的零点为
的零点为 ,
,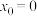 ,请用牛顿切线法求
,请用牛顿切线法求 的2次近似值;
的2次近似值;
(2)已知二次函数 有两个不相等的实数根
有两个不相等的实数根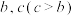 ,数列
,数列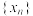 为
为 的牛顿数列,数列
的牛顿数列,数列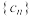 满足
满足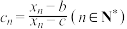 ,且
,且 .
.
(ⅰ)设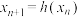 ,求
,求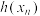 的解析式;
的解析式;
(ⅱ)证明: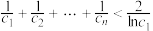
 是
是 的一个零点,任意选取
的一个零点,任意选取 作为
作为 的初始近似值,过点
的初始近似值,过点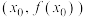 作曲线
作曲线 的切线
的切线 ,
, 与
与 轴的交点为横坐标为
轴的交点为横坐标为 ,称
,称 为
为 的1次近似值,过点
的1次近似值,过点 作曲线
作曲线 的切线
的切线 ,
, 与
与 轴的交点为横坐标为
轴的交点为横坐标为 ,称
,称 为
为 的2次近似值.一般地,过点
的2次近似值.一般地,过点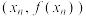 作曲线
作曲线 的切线
的切线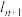 ,
,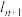 与
与 轴的交点为横坐标为
轴的交点为横坐标为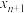 ,就称
,就称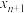 为
为 的
的 次近似值,称数列
次近似值,称数列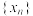 为牛顿数列.
为牛顿数列.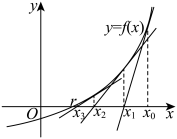
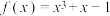 的零点为
的零点为 ,
,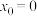 ,请用牛顿切线法求
,请用牛顿切线法求 的2次近似值;
的2次近似值;(2)已知二次函数
 有两个不相等的实数根
有两个不相等的实数根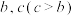 ,数列
,数列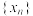 为
为 的牛顿数列,数列
的牛顿数列,数列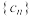 满足
满足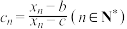 ,且
,且 .
.(ⅰ)设
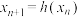 ,求
,求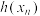 的解析式;
的解析式;(ⅱ)证明:
您最近一年使用:0次
2024-07-10更新
|
477次组卷
|
3卷引用:山东省青岛第三十九中学2023-2024学年高二下学期期末教学质量检测数学试题
解题方法
4 . 拉格朗日中值定理是微分学的基本定理之一,其内容为:如果函数 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且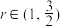 .
.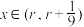 时,
时,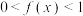 ;
;
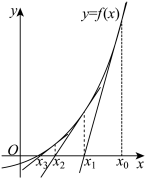
(2)从图形上看,函数 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得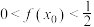 ,然后在点
,然后在点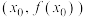 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列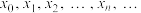 .
.
①当 时,证明:
时,证明: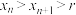 ;
;
②根据①的结论,运用数学归纳法可以证得: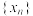 为递减数列,且
为递减数列,且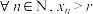 .请以此为前提条件,证明:
.请以此为前提条件,证明: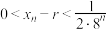 .
.
 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且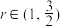 .
.
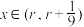 时,
时,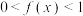 ;
;(2)从图形上看,函数
 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得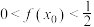 ,然后在点
,然后在点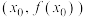 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列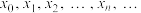 .
.①当
 时,证明:
时,证明: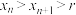 ;
;②根据①的结论,运用数学归纳法可以证得:
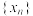 为递减数列,且
为递减数列,且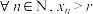 .请以此为前提条件,证明:
.请以此为前提条件,证明: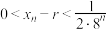 .
.
您最近一年使用:0次
名校
解题方法
5 . 泰勒公式是一个非常重要的数学定理,它可以将一个函数在某一点处展开成无限项的多项式.当 在
在 处的
处的 阶导数都存在时,它的公式表达式如下:
阶导数都存在时,它的公式表达式如下: .注:
.注: 表示函数
表示函数 在原点处的一阶导数,
在原点处的一阶导数, 表示在原点处的二阶导数,以此类推,和
表示在原点处的二阶导数,以此类推,和 表示在原点处的
表示在原点处的 阶导数.
阶导数.
(1)求 的泰勒公式(写到含
的泰勒公式(写到含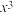 的项为止即可),并估算
的项为止即可),并估算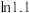 的值(精确到小数点后三位);
的值(精确到小数点后三位);
(2)当 时,比较
时,比较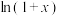 与
与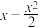 的大小,并证明;
的大小,并证明;
(3)设 ,证明:
,证明: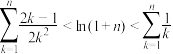 .
.
 在
在 处的
处的 阶导数都存在时,它的公式表达式如下:
阶导数都存在时,它的公式表达式如下: .注:
.注: 表示函数
表示函数 在原点处的一阶导数,
在原点处的一阶导数, 表示在原点处的二阶导数,以此类推,和
表示在原点处的二阶导数,以此类推,和 表示在原点处的
表示在原点处的 阶导数.
阶导数.(1)求
 的泰勒公式(写到含
的泰勒公式(写到含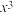 的项为止即可),并估算
的项为止即可),并估算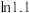 的值(精确到小数点后三位);
的值(精确到小数点后三位);(2)当
 时,比较
时,比较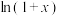 与
与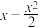 的大小,并证明;
的大小,并证明;(3)设
 ,证明:
,证明: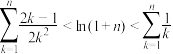 .
.
您最近一年使用:0次
2024-07-20更新
|
293次组卷
|
2卷引用:宁夏回族自治区石嘴山市第三中学2023-2024学年高二下学期7月期末考试数学试题
6 . 柯西不等式是数学家柯西在研究数学分析中的“流数”问题时得到的,其形式为: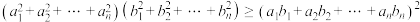 ,等号成立条件为
,等号成立条件为 或
或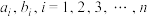 至少有一方全为0.柯西不等式用处很广,高中阶段常用来计算或证明表达式的最值问题.已知数列
至少有一方全为0.柯西不等式用处很广,高中阶段常用来计算或证明表达式的最值问题.已知数列 满足
满足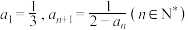 .
.
(1)证明:数列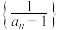 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(2)证明: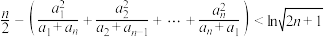 .
.
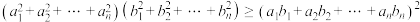 ,等号成立条件为
,等号成立条件为 或
或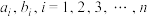 至少有一方全为0.柯西不等式用处很广,高中阶段常用来计算或证明表达式的最值问题.已知数列
至少有一方全为0.柯西不等式用处很广,高中阶段常用来计算或证明表达式的最值问题.已知数列 满足
满足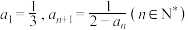 .
.(1)证明:数列
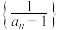 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;(2)证明:
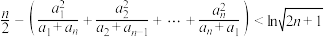 .
.
您最近一年使用:0次
7 . 帕德近似是法国数学家亨利・帕德发明的用有理多项式近似特定函数的方法.给定两个正整数 ,函数
,函数 在
在 处的
处的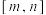 阶帕德近似定义为:
阶帕德近似定义为: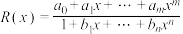 且满足:
且满足: .
.
注: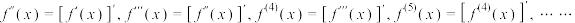 .
.
已知函数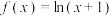 在
在 处的
处的 阶帕德近似
阶帕德近似 .
.
(1)求 的表达式;
的表达式;
(2)记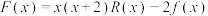 ,当
,当 时,证明不等式
时,证明不等式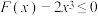 ;
;
(3)当 ,且
,且 时,证明不等式
时,证明不等式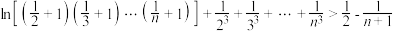 .
.
 ,函数
,函数 在
在 处的
处的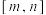 阶帕德近似定义为:
阶帕德近似定义为: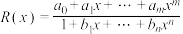 且满足:
且满足: .
.注:
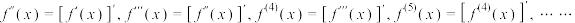 .
.已知函数
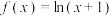 在
在 处的
处的 阶帕德近似
阶帕德近似 .
.(1)求
 的表达式;
的表达式;(2)记
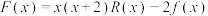 ,当
,当 时,证明不等式
时,证明不等式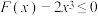 ;
;(3)当
 ,且
,且 时,证明不等式
时,证明不等式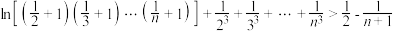 .
.
您最近一年使用:0次
名校
解题方法
8 . 罗尔定理是高等代数中微积分的三大定理之一,它与导数和函数的零点有关,是由法国数学家米歇尔·罗尔于1691年提出的.它的表达如下:如果函数 满足在闭区间
满足在闭区间 连续,在开区间
连续,在开区间 内可导,且
内可导,且 ,那么在区间
,那么在区间 内至少存在一点
内至少存在一点 ,使得
,使得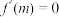 .
.
(1)运用罗尔定理证明:若函数 在区间
在区间 连续,在区间
连续,在区间 上可导,则存在
上可导,则存在 ,使得
,使得 .
.
(2)已知函数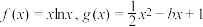 ,若对于区间
,若对于区间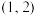 内任意两个不相等的实数
内任意两个不相等的实数 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(3)证明:当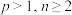 时,有
时,有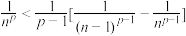 .
.
 满足在闭区间
满足在闭区间 连续,在开区间
连续,在开区间 内可导,且
内可导,且 ,那么在区间
,那么在区间 内至少存在一点
内至少存在一点 ,使得
,使得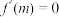 .
.(1)运用罗尔定理证明:若函数
 在区间
在区间 连续,在区间
连续,在区间 上可导,则存在
上可导,则存在 ,使得
,使得 .
.(2)已知函数
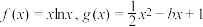 ,若对于区间
,若对于区间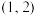 内任意两个不相等的实数
内任意两个不相等的实数 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.(3)证明:当
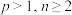 时,有
时,有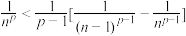 .
.
您最近一年使用:0次
2024-04-06更新
|
1713次组卷
|
3卷引用:湖北省咸宁市2023-2024学年高二下学期期末考试数学试卷



