1 . 已知数列 满足
满足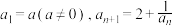 .
.
(1)若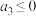 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若当 时,都有
时,都有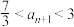 ,求实数
,求实数 的取值范围;
的取值范围;
(3)设数列 满足
满足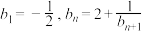 ,求证:
,求证: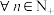 ,若
,若 ,则数列
,则数列 的项数必有限.
的项数必有限.
 满足
满足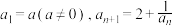 .
.(1)若
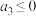 ,求实数
,求实数 的取值范围;
的取值范围;(2)若当
 时,都有
时,都有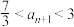 ,求实数
,求实数 的取值范围;
的取值范围;(3)设数列
 满足
满足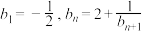 ,求证:
,求证: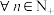 ,若
,若 ,则数列
,则数列 的项数必有限.
的项数必有限.
您最近一年使用:0次
名校
解题方法
2 . 已知函数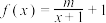 ,
,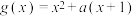 .
.
(1)当 ,
, 时,解关于
时,解关于 的不等式
的不等式 ;
;
(2)当 时,对任意
时,对任意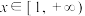 ,关于
,关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 ,
, 时,若点
时,若点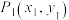 ,
,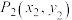 均为函数
均为函数 与函数
与函数 图象的公共点,且
图象的公共点,且 ,求证:
,求证: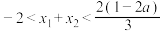 .
.
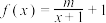 ,
,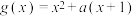 .
.(1)当
 ,
, 时,解关于
时,解关于 的不等式
的不等式 ;
;(2)当
 时,对任意
时,对任意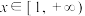 ,关于
,关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)当
 ,
, 时,若点
时,若点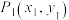 ,
,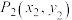 均为函数
均为函数 与函数
与函数 图象的公共点,且
图象的公共点,且 ,求证:
,求证: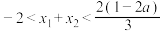 .
.
您最近一年使用:0次
2024-08-14更新
|
549次组卷
|
3卷引用:四川德阳市博雅明德高级中学2023-2024学年高三高考适应性考试数学试题
3 . 我们可以用“配方法”和“主元法”等方法证明“二元不等式”: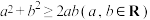 ,当且仅当
,当且仅当 时,
时, 等号成立.
等号成立.
(1)证明“三元不等式”: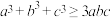
 .
.
(2)已知函数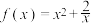 .
.
①解不等式 ;
;
②对任意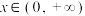 ,
,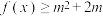 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
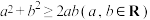 ,当且仅当
,当且仅当 时,
时, 等号成立.
等号成立.(1)证明“三元不等式”:
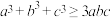
 .
.(2)已知函数
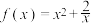 .
.①解不等式
 ;
;②对任意
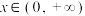 ,
,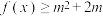 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-10-11更新
|
295次组卷
|
2卷引用:江苏省镇江市2024-2025学年高三上学期期初考试数学试卷
解题方法
4 . 已知 克糖水中含有
克糖水中含有 克糖
克糖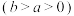 ,再添加
,再添加 克糖
克糖 (假设全部溶解),糖水变甜了,
(假设全部溶解),糖水变甜了,
(1)请将这一事实表示为一个不等式,并证明这个不等式成立;
(2)运用该不等式比较以下三个值的大小: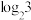 ,
, ,
,
 克糖水中含有
克糖水中含有 克糖
克糖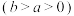 ,再添加
,再添加 克糖
克糖 (假设全部溶解),糖水变甜了,
(假设全部溶解),糖水变甜了,(1)请将这一事实表示为一个不等式,并证明这个不等式成立;
(2)运用该不等式比较以下三个值的大小:
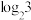 ,
, ,
,
您最近一年使用:0次
真题
5 . 已知实数p满足不等式 ,试判断方程
,试判断方程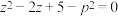 有无实根,并给出证明.
有无实根,并给出证明.
 ,试判断方程
,试判断方程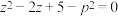 有无实根,并给出证明.
有无实根,并给出证明.
您最近一年使用:0次
6 . 对于项数为 ,
,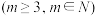 的有限数列
的有限数列 ,记该数列前i项
,记该数列前i项 、
、 、
、 、
、 中的最大项为
中的最大项为 ,
,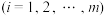 即
即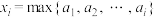 ;该数列后
;该数列后 项
项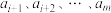 中的最小项为
中的最小项为 ,
,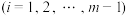 ,即
,即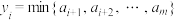 ,
,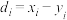 ,
,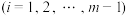 .例如数列:1、3、2,则
.例如数列:1、3、2,则 ,
,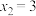 ,
, ;
; ,
, ;
; ,
, .
.
(1)若四项数列 满足
满足 ,
, ,
, ,
, ,求
,求 、
、 、
、 、
、 ;
;
(2)设c为常数,且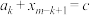 ,
,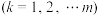 ,求证:
,求证: ,
,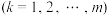 ;
;
(3)设实数 ,数列
,数列 满足
满足 ,
,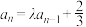 ,
,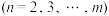 ,若数列
,若数列 对应的
对应的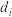 满足
满足 对任意的正整数
对任意的正整数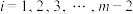 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 ,
,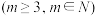 的有限数列
的有限数列 ,记该数列前i项
,记该数列前i项 、
、 、
、 、
、 中的最大项为
中的最大项为 ,
,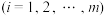 即
即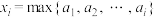 ;该数列后
;该数列后 项
项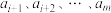 中的最小项为
中的最小项为 ,
,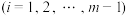 ,即
,即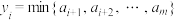 ,
,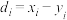 ,
,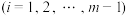 .例如数列:1、3、2,则
.例如数列:1、3、2,则 ,
,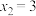 ,
, ;
; ,
, ;
; ,
, .
.(1)若四项数列
 满足
满足 ,
, ,
, ,
, ,求
,求 、
、 、
、 、
、 ;
;(2)设c为常数,且
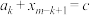 ,
,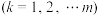 ,求证:
,求证: ,
,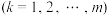 ;
;(3)设实数
 ,数列
,数列 满足
满足 ,
,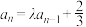 ,
,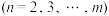 ,若数列
,若数列 对应的
对应的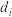 满足
满足 对任意的正整数
对任意的正整数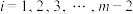 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
7 . 已知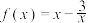 .
.
(1)求不等式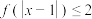 的解集;
的解集;
(2)若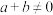 ,且
,且 ,求证:
,求证: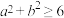 .
.
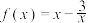 .
.(1)求不等式
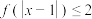 的解集;
的解集;(2)若
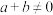 ,且
,且 ,求证:
,求证: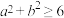 .
.
您最近一年使用:0次
2022-03-28更新
|
576次组卷
|
5卷引用:陕西省西安八校2022届高三下学期第二次联考文科数学试题
8 . 已知函数 对任意
对任意 都有
都有 ,且当
,且当 时,
时,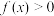 .
.
(1)证明: 为定义在
为定义在 上的单调递增奇函数;
上的单调递增奇函数;
(2)若 ,求
,求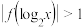 的解集.
的解集.
 对任意
对任意 都有
都有 ,且当
,且当 时,
时,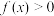 .
.(1)证明:
 为定义在
为定义在 上的单调递增奇函数;
上的单调递增奇函数;(2)若
 ,求
,求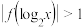 的解集.
的解集.
您最近一年使用:0次
名校
解题方法
9 . 已知数列 的前
的前 项和为
项和为 ,且对一切正整数
,且对一切正整数 都有
都有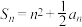 .
.
(1)求证: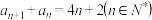 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)是否存在实数 ,使不等式
,使不等式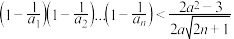 ,对一切正整数
,对一切正整数 都成立?若存在,求出
都成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
 的前
的前 项和为
项和为 ,且对一切正整数
,且对一切正整数 都有
都有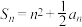 .
.(1)求证:
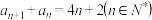 ;
;(2)求数列
 的通项公式;
的通项公式;(3)是否存在实数
 ,使不等式
,使不等式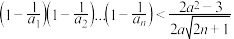 ,对一切正整数
,对一切正整数 都成立?若存在,求出
都成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
您最近一年使用:0次
2020-07-09更新
|
720次组卷
|
3卷引用:江苏省南通市海安高级中学2020届高三下学期5月第二次检测数学试题
江苏省南通市海安高级中学2020届高三下学期5月第二次检测数学试题江苏省盐城中学2022-2023学年高三上学期9月月考数学试题(已下线)专题1 数列的单调性 微点5 数列单调性的判断方法(五)——递推法
10 . 已知等差数列 的首项为p,公差为
的首项为p,公差为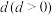 ,对于不同的自然数
,对于不同的自然数 ,直线
,直线 与
与 轴和指数函数
轴和指数函数 的图象分别交于点
的图象分别交于点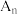 与
与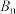 (如图所示),记
(如图所示),记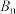 的坐标为
的坐标为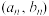 ,直角梯形
,直角梯形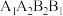 、
、 的面积分别为
的面积分别为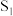 和
和 ,一般地记直角梯形
,一般地记直角梯形 的面积为
的面积为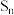 .
.

(1)求证:数列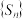 是公比绝对值小于1的等比数列;
是公比绝对值小于1的等比数列;
(2)设 的公差
的公差 ,是否存在这样的正整数
,是否存在这样的正整数 ,构成以
,构成以 ,
,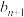 ,
, 为边长的三角形?并请说明理由;
为边长的三角形?并请说明理由;
(3)设 的公差
的公差 为已知常数,是否存在这样的实数p使得(1)中无穷等比数列
为已知常数,是否存在这样的实数p使得(1)中无穷等比数列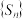 各项的和
各项的和 ?并请说明理由.
?并请说明理由.
 的首项为p,公差为
的首项为p,公差为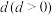 ,对于不同的自然数
,对于不同的自然数 ,直线
,直线 与
与 轴和指数函数
轴和指数函数 的图象分别交于点
的图象分别交于点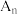 与
与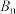 (如图所示),记
(如图所示),记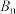 的坐标为
的坐标为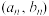 ,直角梯形
,直角梯形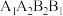 、
、 的面积分别为
的面积分别为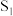 和
和 ,一般地记直角梯形
,一般地记直角梯形 的面积为
的面积为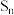 .
.
(1)求证:数列
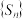 是公比绝对值小于1的等比数列;
是公比绝对值小于1的等比数列;(2)设
 的公差
的公差 ,是否存在这样的正整数
,是否存在这样的正整数 ,构成以
,构成以 ,
,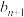 ,
, 为边长的三角形?并请说明理由;
为边长的三角形?并请说明理由;(3)设
 的公差
的公差 为已知常数,是否存在这样的实数p使得(1)中无穷等比数列
为已知常数,是否存在这样的实数p使得(1)中无穷等比数列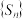 各项的和
各项的和 ?并请说明理由.
?并请说明理由.
您最近一年使用:0次



