名校
解题方法
1 . 一种锥底孵化桶常用于鱼虾类的孵化,其桶底采用上大下小的漏斗状设计,底部设计成锥形便于收集幼苗.铁匠老张准备用一个半径 为的扇形铁片作为圆锥的侧面,制作成一个圆锥形无盖漏斗(接缝处忽略不计).若该漏斗的容积为
为的扇形铁片作为圆锥的侧面,制作成一个圆锥形无盖漏斗(接缝处忽略不计).若该漏斗的容积为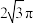 ,且漏斗的顶点及底面圆周都在球O的表面上,则当R最小时,球O的表面积为( )
,且漏斗的顶点及底面圆周都在球O的表面上,则当R最小时,球O的表面积为( )
 为的扇形铁片作为圆锥的侧面,制作成一个圆锥形无盖漏斗(接缝处忽略不计).若该漏斗的容积为
为的扇形铁片作为圆锥的侧面,制作成一个圆锥形无盖漏斗(接缝处忽略不计).若该漏斗的容积为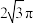 ,且漏斗的顶点及底面圆周都在球O的表面上,则当R最小时,球O的表面积为( )
,且漏斗的顶点及底面圆周都在球O的表面上,则当R最小时,球O的表面积为( )A. | B. | C.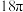 | D.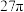 |
您最近一年使用:0次
2024-04-24更新
|
431次组卷
|
2卷引用:陕西省安康市高新中学、安康中学高新分校2023-2024学年高三阶段性测试(八)理科数学试题
2 . 所有的顶点都在两个平行平面内的多面体叫做拟柱体,其中平行的两个面叫底面,其它面叫侧面,两底面之间的距离叫高,经过高的中点且平行于两个底面的截面叫中截面.似柱体的体积公式为 ,这里
,这里 、
、 为两个底面面积,
为两个底面面积, 为中截面面积,
为中截面面积, 为高.如图,已知多面体
为高.如图,已知多面体 中,
中, 是边长
是边长 为的正方形,且
为的正方形,且 ,
,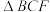 均为正三角形,
均为正三角形,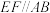 ,
,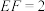 ,则该多面体的体积为( )
,则该多面体的体积为( )
 ,这里
,这里 、
、 为两个底面面积,
为两个底面面积, 为中截面面积,
为中截面面积, 为高.如图,已知多面体
为高.如图,已知多面体 中,
中, 是边长
是边长 为的正方形,且
为的正方形,且 ,
,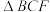 均为正三角形,
均为正三角形,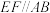 ,
,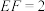 ,则该多面体的体积为( )
,则该多面体的体积为( )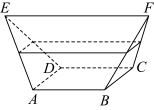
A. | B.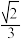 | C.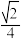 | D. |
您最近一年使用:0次
2024-03-06更新
|
548次组卷
|
4卷引用:浙江省杭十四中学2023-2024学年高二上学期期末数学试题
浙江省杭十四中学2023-2024学年高二上学期期末数学试题(已下线)第六章 突破立体几何创新问题 专题一 交汇中国古代文化 微点2 与中国古代文化遗产有关的立体几何问题(二)【基础版】(已下线)8.3简单几何体的表面积与体积【第三练】“上好三节课,做好三套题“高中数学素养晋级之路2024年新高考Ⅰ卷浙大优学靶向精准模拟数学试题(五)
名校
3 . 2022年卡塔尔足球世界杯吸引了全世界许多球迷的关注,足球最早起源于我国古代“蹴鞠”,被列为国家级非物质文化,蹴即踢,鞠即球,北宋《宋太祖蹴鞠图》描绘太祖、太宗和臣子们蹴鞠的场景.已知某“鞠”的表面上有四个点A,B,C,D,连接这四点构成三棱锥 如图所示,顶点A在底面的射影落在△BCD内,它的体积为
如图所示,顶点A在底面的射影落在△BCD内,它的体积为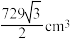 ,其中△BCD和△ABC都是边长为
,其中△BCD和△ABC都是边长为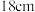 的正三角形,则该“鞠”的表面积为( )
的正三角形,则该“鞠”的表面积为( )
 如图所示,顶点A在底面的射影落在△BCD内,它的体积为
如图所示,顶点A在底面的射影落在△BCD内,它的体积为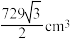 ,其中△BCD和△ABC都是边长为
,其中△BCD和△ABC都是边长为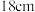 的正三角形,则该“鞠”的表面积为( )
的正三角形,则该“鞠”的表面积为( )
A.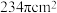 | B.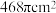 | C.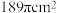 | D.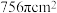 |
您最近一年使用:0次
2023-08-10更新
|
569次组卷
|
7卷引用:湖南省新高考教学教研联盟2022-2023学年高二下学期5月联考数学试题
湖南省新高考教学教研联盟2022-2023学年高二下学期5月联考数学试题江苏省江阴市第一中学2024届高三上学期12月阶段测试数学试题江苏省镇江市扬中市第二高级中学2024届高三上学期期末模拟数学试卷(二)(已下线)技巧03 数学文化与数学阅读解题技巧(4大核心考点)(讲义)(已下线)第六章 突破立体几何创新问题 专题一 交汇中国古代文化 微点4 与中国古代文化遗产有关的立体几何问题综合训练【基础版】(已下线)第六章 突破立体几何创新问题 专题二 融合科技、社会热点 微点3 融合科技、社会热点等现代文化的立体几何和问题综合训练【培优版】(已下线)专题06 空间直线﹑平面的垂直(一-《知识解读·题型专练》(人教A版2019必修第二册)
解题方法
4 . 魏晋时期著名数学家刘徽解释了《九章算术-商功》中记录的空间几何体“堑堵、阳马、鳖臑”的形状和产生过程,即:“邪解立方得两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也”,其意思是:把正方体或长方体斜向分解成两个堑堵,再把堑堵斜向分解得到一个阳马和一个鳖臑,两者的体积比为定值.如图,在长方体 被平面
被平面 截得两个“堑堵”,其中一个“堑堵”
截得两个“堑堵”,其中一个“堑堵” 又被平面
又被平面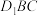 截为一个“阳马”
截为一个“阳马”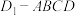 和一个“鳖臑”
和一个“鳖臑”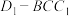 ,则下列说法正确的是( )
,则下列说法正确的是( )

 被平面
被平面 截得两个“堑堵”,其中一个“堑堵”
截得两个“堑堵”,其中一个“堑堵” 又被平面
又被平面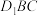 截为一个“阳马”
截为一个“阳马”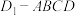 和一个“鳖臑”
和一个“鳖臑”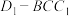 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.“阳马”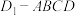 是一个底面为矩形,且有一条侧棱垂直于底面的四棱锥,“鳖臑” 是一个底面为矩形,且有一条侧棱垂直于底面的四棱锥,“鳖臑”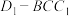 为四个面全是直角三角形的三棱锥 为四个面全是直角三角形的三棱锥 |
B.“阳马”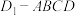 的体积是“鳖臑” 的体积是“鳖臑”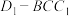 的体积的2倍 的体积的2倍 |
C.“阳马”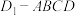 的最长棱和“鳖臑” 的最长棱和“鳖臑”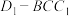 的最长棱不相等 的最长棱不相等 |
D.若 ,“鳖臑” ,“鳖臑”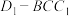 的所有顶点都在同一球面上,且该球的表面积为 的所有顶点都在同一球面上,且该球的表面积为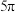 ,则长方体 ,则长方体 的体积的最大值为2 的体积的最大值为2 |
您最近一年使用:0次
5 . 《九章算术・商功》刘徽注:“邪解立方得二堑堵,邪解堑堵,其一为阳马,其一为鳖臑,”阳马,是底面为长方形或正方形,有一条侧棱垂直底面的四棱锥.在 底面
底面 ,且底面
,且底面 为正方形的阳马中,若
为正方形的阳马中,若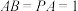 ,则( )
,则( )
 底面
底面 ,且底面
,且底面 为正方形的阳马中,若
为正方形的阳马中,若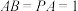 ,则( )
,则( )A.直线 与直线 与直线 所成角为 所成角为 |
B.异面直线 与直线 与直线 的距离为 的距离为 |
C.四棱锥 的体积为1 的体积为1 |
D.直线 与底面 与底面 所成角的余弦值为 所成角的余弦值为 |
您最近一年使用:0次
6 . 数学史上著名的波尔约-格维也纳定理:任意两个面积相等的多边形,它们可以通过相互拼接得到.它由法卡斯·波尔约(FarksBolyai)和保罗·格维也纳(PaulGerwien)两位数学家分别在1833年和1835年给出证明.现在我们来尝试用平面图形拼接空间图形,使它们的全面积都与原平面图形的面积相等:(1)给出两块相同的正三角形纸片(如图1、图2),其中图1,沿正三角形三边中点连线折起,可拼得一个正三棱锥;图2,正三角形三个角上剪出三个相同的四边形(阴影部分),其较长的一组邻边边长为三角形边长的 ,有一组对角为直角,余下部分按虚线折起,可成一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱锥的上底.
,有一组对角为直角,余下部分按虚线折起,可成一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱锥的上底.
(1)试比较图1与图2剪拼的正三棱锥与正三棱柱的体积的大小;
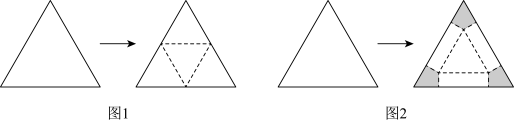
(2)如果给出的是一块任意三角形的纸片(如图3),要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等.请仿照图2设计剪拼方案,用虚线标示在图3中,并作简要说明.
 ,有一组对角为直角,余下部分按虚线折起,可成一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱锥的上底.
,有一组对角为直角,余下部分按虚线折起,可成一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱锥的上底.
(1)试比较图1与图2剪拼的正三棱锥与正三棱柱的体积的大小;
(2)如果给出的是一块任意三角形的纸片(如图3),要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等.请仿照图2设计剪拼方案,用虚线标示在图3中,并作简要说明.

您最近一年使用:0次
7 . 中国古代数学家很早就对空间几何体进行了系统的研究,中国传世数学著作《九章算术》卷五“商功”主要讲述了以立体问题为主的各种形体体积的计算公式.例如在推导正四棱台(古人称方台)体积公式时,将正四棱台切割成九部分进行求解.下图(1)为俯视图,图(2)为立体切面图. 对应的是正四棱台中间位置的长方体;
对应的是正四棱台中间位置的长方体;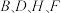 对应四个三棱柱,
对应四个三棱柱, 对应四个四棱锥.若这四个三棱柱的体积之和为12,四个四棱锥的体积之和为4,则该正四棱台的体积为( )
对应四个四棱锥.若这四个三棱柱的体积之和为12,四个四棱锥的体积之和为4,则该正四棱台的体积为( )
 对应的是正四棱台中间位置的长方体;
对应的是正四棱台中间位置的长方体; 对应四个三棱柱,
对应四个三棱柱, 对应四个四棱锥.若这四个三棱柱的体积之和为12,四个四棱锥的体积之和为4,则该正四棱台的体积为( )
对应四个四棱锥.若这四个三棱柱的体积之和为12,四个四棱锥的体积之和为4,则该正四棱台的体积为( )
| A.24 | B.28 | C.32 | D.36 |
您最近一年使用:0次
2023-05-03更新
|
1273次组卷
|
6卷引用:福建省宁德市普通高中2023届高三质量检测数学试题
名校
解题方法
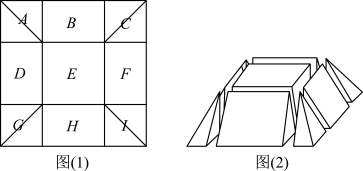
8 . “牟合方盖”是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法,当一个正方体用圆柱从纵横两侧面作内切圆柱体时,两圆柱体的公共部分即为“牟合方盖”,他提出“牟合方盖”的内切球的体积与“牟合方盖”的体积比为定值.南北朝时期祖暅提出理论:“缘幂势既同,则积不容异”,即“在等高处的截面面积总是相等的几何体,它们的体积也相等”,并算出了“牟合方盖”和球的体积.其大体思想可用如图表示,其中图1为棱长为 的正方体截得的“牟合方盖”的八分之一,图2为棱长为
的正方体截得的“牟合方盖”的八分之一,图2为棱长为 的正方体的八分之一,图3是以底面边长为
的正方体的八分之一,图3是以底面边长为 的正方体的一个底面和底面以外的一个顶点作的四棱锥,则根据祖暅原理,下列结论正确的是:( )
的正方体的一个底面和底面以外的一个顶点作的四棱锥,则根据祖暅原理,下列结论正确的是:( )
 的正方体截得的“牟合方盖”的八分之一,图2为棱长为
的正方体截得的“牟合方盖”的八分之一,图2为棱长为 的正方体的八分之一,图3是以底面边长为
的正方体的八分之一,图3是以底面边长为 的正方体的一个底面和底面以外的一个顶点作的四棱锥,则根据祖暅原理,下列结论正确的是:( )
的正方体的一个底面和底面以外的一个顶点作的四棱锥,则根据祖暅原理,下列结论正确的是:( )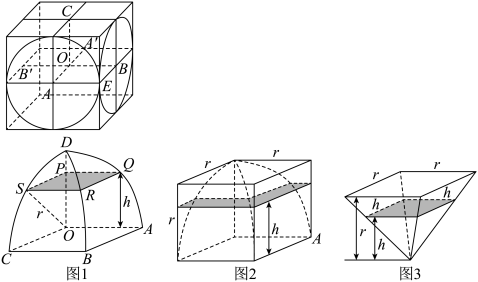
| A.若以一个平行于正方体上下底面的平面,截“牟合方盖”,截面是一个圆形 |
B.图2中阴影部分的面积为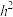 |
C.“牟合方盖”的内切球的体积与“牟合方盖”的体积比为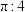 |
D.由棱长为 的正方体截得的“牟合方盖”体积为 的正方体截得的“牟合方盖”体积为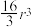 |
您最近一年使用:0次
2023-05-01更新
|
2655次组卷
|
8卷引用:云南省昆明市第一中学2023届高三第九次考前适应性训练数学试题
云南省昆明市第一中学2023届高三第九次考前适应性训练数学试题(已下线)模块六 专题12 易错题目重组卷(云南卷)湖南省衡阳市第八中学2023届高三高考适应性考试数学试题浙江省温州市第五十一中学2024届高三上学期期末数学试题(已下线)最新模拟重组精华卷2 -模块一 各地期末考试精选汇编(已下线)新题型01 新高考新结构二十一大考点汇总-2(已下线)第二章 立体几何中的计算 专题三 空间体积的计算 微点2 祖暅原理及球体积辅助体综合训练【培优版】(已下线)专题1 立体几何中的截面问题【讲】(压轴小题)
9 . 南北朝时期的伟大科学家祖暅,于五世纪末提出了体积计算原理,即祖暅原理:“夫叠棋成立积,缘幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么,这两个几何体的体积相等.其最著名之处是解决了“牟合方盖”的体积问题.如图所示,正方体 ,棱长为
,棱长为 .
.
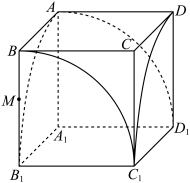
(1)求图中四分之一圆柱体 的体积;
的体积;
(2)在图中画出四分之一圆柱体 与四分之一圆柱体
与四分之一圆柱体 的一条交线(不要求说明理由);
的一条交线(不要求说明理由);
(3)四分之一圆柱体 与四分之一圆柱体
与四分之一圆柱体 公共部分是八分之一个“牟合方盖”.点
公共部分是八分之一个“牟合方盖”.点 在棱
在棱 上,设
上,设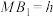 .过点
.过点 作一个与正方体底面
作一个与正方体底面 平行的平面,求该截面位于八分之一“牟合方盖”内部分的面积;
平行的平面,求该截面位于八分之一“牟合方盖”内部分的面积;
(4)如果令 ,求出八分之一“牟合方盖”的体积.
,求出八分之一“牟合方盖”的体积.
 ,棱长为
,棱长为 .
.
(1)求图中四分之一圆柱体
 的体积;
的体积;(2)在图中画出四分之一圆柱体
 与四分之一圆柱体
与四分之一圆柱体 的一条交线(不要求说明理由);
的一条交线(不要求说明理由);(3)四分之一圆柱体
 与四分之一圆柱体
与四分之一圆柱体 公共部分是八分之一个“牟合方盖”.点
公共部分是八分之一个“牟合方盖”.点 在棱
在棱 上,设
上,设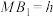 .过点
.过点 作一个与正方体底面
作一个与正方体底面 平行的平面,求该截面位于八分之一“牟合方盖”内部分的面积;
平行的平面,求该截面位于八分之一“牟合方盖”内部分的面积;(4)如果令
 ,求出八分之一“牟合方盖”的体积.
,求出八分之一“牟合方盖”的体积.
您最近一年使用:0次
2023-04-21更新
|
850次组卷
|
7卷引用:山西省阳泉市第十一中学校2022-2023学年高一下学期期中数学试题
山西省阳泉市第十一中学校2022-2023学年高一下学期期中数学试题(已下线)重难点专题02 空间点直线平面之间的位置关系-【同步题型讲义】山西省晋中市2022-2023学年高一下学期期中数学试题山西省长治市2022-2023学年高一下学期期中数学试题(已下线)压轴题立体几何新定义题(九省联考第19题模式)练(已下线)第二章 立体几何中的计算 专题三 空间体积的计算 微点2 祖暅原理及球体积辅助体综合训练【培优版】(已下线)模块四 专题2 高考新题型专练(新定义专练)(人教A)
名校
10 . 《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马.如图正方体 的棱长为2,点
的棱长为2,点 是该正方体的侧面
是该正方体的侧面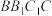 上的一个动点(含边界),且
上的一个动点(含边界),且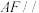 平面
平面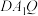 ,
, ,
, 分别是棱
分别是棱 ,
, 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )
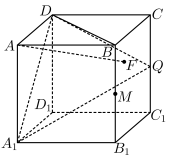
 的棱长为2,点
的棱长为2,点 是该正方体的侧面
是该正方体的侧面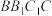 上的一个动点(含边界),且
上的一个动点(含边界),且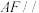 平面
平面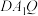 ,
, ,
, 分别是棱
分别是棱 ,
, 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )
A.直线 与直线 与直线 不可能垂直 不可能垂直 |
B.三棱锥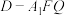 的体积为定值 的体积为定值 |
C.直线 与平面 与平面 所成角的正弦值的最大值为 所成角的正弦值的最大值为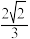 |
D.阳马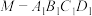 的外接球 的外接球 与内切球 与内切球 的半径之比为 的半径之比为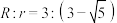 |
您最近一年使用:0次
2023-04-15更新
|
632次组卷
|
5卷引用:浙江省衢温5+1联盟2022-2023学年高二下学期期中联考数学试题
浙江省衢温5+1联盟2022-2023学年高二下学期期中联考数学试题海南省琼海市嘉积中学2023届高三高考模拟预测数学试题(已下线)模块四 专题8 高考新题型(复杂情景题专训)拔高能力练(人教A)(已下线)模块一 专题1 《立体几何》单元检测篇 B提升卷(已下线)模块三 专题1 题型突破篇 小题入门夯实练(1)期末终极研习室(2023-2024学年第一学期)高三



