名校
解题方法
1 . 已知椭圆C: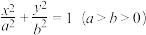 的离心率为
的离心率为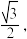 长轴的右端点为
长轴的右端点为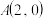 .
.
(1)求C的方程;
(2)不经过点A的直线 与椭圆C分别相交于
与椭圆C分别相交于 两点,且以MN为直径的圆过点
两点,且以MN为直径的圆过点 ,
,
①试证明直线 过一定点,并求出此定点;
过一定点,并求出此定点;
②从点 作
作 垂足为
垂足为 ,点
,点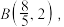 写出
写出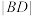 的最小值(结论不要求证明).
的最小值(结论不要求证明).
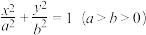 的离心率为
的离心率为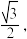 长轴的右端点为
长轴的右端点为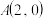 .
.(1)求C的方程;
(2)不经过点A的直线
 与椭圆C分别相交于
与椭圆C分别相交于 两点,且以MN为直径的圆过点
两点,且以MN为直径的圆过点 ,
,①试证明直线
 过一定点,并求出此定点;
过一定点,并求出此定点;②从点
 作
作 垂足为
垂足为 ,点
,点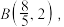 写出
写出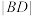 的最小值(结论不要求证明).
的最小值(结论不要求证明).
您最近一年使用:0次
名校
2 . 在平面直角坐标系 中,已知圆C:
中,已知圆C: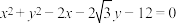 ,
, ,
,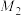 是圆
是圆 上的动点,且
上的动点,且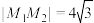 ,
,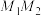 的中点为
的中点为 .
.
(1)求点 的轨迹方程;
的轨迹方程;
(2)设点A是直线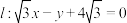 上的动点,
上的动点, ,
, 是
是 的轨迹的两条切线,
的轨迹的两条切线, ,
, 为切点,求四边形
为切点,求四边形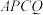 面积的最小值;
面积的最小值;
(3)若垂直于 轴的直线
轴的直线 过点
过点 且与
且与 的轨迹交于点
的轨迹交于点 ,
, ,点
,点 为直线
为直线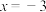 上的动点,直线
上的动点,直线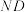 ,
,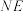 与
与 的轨迹的另一个交点分别为
的轨迹的另一个交点分别为 ,
,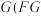 与
与 不重合),求证:直线
不重合),求证:直线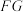 过定点.
过定点.
 中,已知圆C:
中,已知圆C: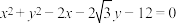 ,
, ,
,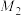 是圆
是圆 上的动点,且
上的动点,且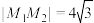 ,
,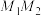 的中点为
的中点为 .
.(1)求点
 的轨迹方程;
的轨迹方程;(2)设点A是直线
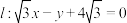 上的动点,
上的动点, ,
, 是
是 的轨迹的两条切线,
的轨迹的两条切线, ,
, 为切点,求四边形
为切点,求四边形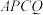 面积的最小值;
面积的最小值;(3)若垂直于
 轴的直线
轴的直线 过点
过点 且与
且与 的轨迹交于点
的轨迹交于点 ,
, ,点
,点 为直线
为直线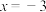 上的动点,直线
上的动点,直线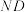 ,
,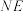 与
与 的轨迹的另一个交点分别为
的轨迹的另一个交点分别为 ,
,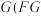 与
与 不重合),求证:直线
不重合),求证:直线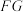 过定点.
过定点.
您最近一年使用:0次
3 . 已知以点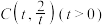 为圆心的圆经过原点O,且与x轴交于另一点A,与y轴交于另一点B.
为圆心的圆经过原点O,且与x轴交于另一点A,与y轴交于另一点B.
(1)求证: 为定值
为定值
(2)设直线 与圆C交于点M,N,若
与圆C交于点M,N,若 ,求圆C的方程.
,求圆C的方程.
(3)在(2)的条件下,设P,Q分别是直线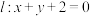 和圆C上的动点,求
和圆C上的动点,求 的最小值及此时点P的坐标.
的最小值及此时点P的坐标.
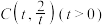 为圆心的圆经过原点O,且与x轴交于另一点A,与y轴交于另一点B.
为圆心的圆经过原点O,且与x轴交于另一点A,与y轴交于另一点B.(1)求证:
 为定值
为定值(2)设直线
 与圆C交于点M,N,若
与圆C交于点M,N,若 ,求圆C的方程.
,求圆C的方程.(3)在(2)的条件下,设P,Q分别是直线
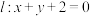 和圆C上的动点,求
和圆C上的动点,求 的最小值及此时点P的坐标.
的最小值及此时点P的坐标.
您最近一年使用:0次
4 . 如图,在平面直角坐标系 中,已知抛物线
中,已知抛物线 :
: .
. 在
在 :
: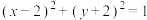 上,记G的几何中心为点
上,记G的几何中心为点 ,则当
,则当 取得最大值时,求点
取得最大值时,求点 的坐标.
的坐标.
(2)已知动点 、
、 在C上,分别过
在C上,分别过 、
、 作抛物线的切线
作抛物线的切线 、
、 ,设
,设 和
和 相交于点T,若点T恒在直线
相交于点T,若点T恒在直线 :
: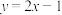 上,求证:直线
上,求证:直线 经过定点.
经过定点.
(3)将 绕原点顺时针旋转90°得到
绕原点顺时针旋转90°得到 ,给定点
,给定点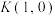 ,
, 上有四点
上有四点 、
、 、
、 、
、 ,满足
,满足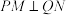 ,
,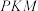 、
、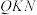 均三点共线,且
均三点共线,且 、
、 都在x轴上方,设线段
都在x轴上方,设线段 和
和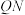 的中点分别为T、S,试判断:直线
的中点分别为T、S,试判断:直线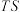 是否会经过一个定点?若会,请求出这个定点的坐标,若不会,请说明理由.
是否会经过一个定点?若会,请求出这个定点的坐标,若不会,请说明理由.
 中,已知抛物线
中,已知抛物线 :
: .
.
 在
在 :
: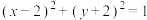 上,记G的几何中心为点
上,记G的几何中心为点 ,则当
,则当 取得最大值时,求点
取得最大值时,求点 的坐标.
的坐标.(2)已知动点
 、
、 在C上,分别过
在C上,分别过 、
、 作抛物线的切线
作抛物线的切线 、
、 ,设
,设 和
和 相交于点T,若点T恒在直线
相交于点T,若点T恒在直线 :
: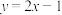 上,求证:直线
上,求证:直线 经过定点.
经过定点.(3)将
 绕原点顺时针旋转90°得到
绕原点顺时针旋转90°得到 ,给定点
,给定点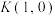 ,
, 上有四点
上有四点 、
、 、
、 、
、 ,满足
,满足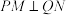 ,
,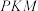 、
、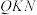 均三点共线,且
均三点共线,且 、
、 都在x轴上方,设线段
都在x轴上方,设线段 和
和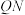 的中点分别为T、S,试判断:直线
的中点分别为T、S,试判断:直线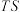 是否会经过一个定点?若会,请求出这个定点的坐标,若不会,请说明理由.
是否会经过一个定点?若会,请求出这个定点的坐标,若不会,请说明理由.
您最近一年使用:0次
5 . 已知圆 ,直线
,直线 .
.
(1)求证:直线 恒过定点.
恒过定点.
(2)直线 被圆
被圆 截得的弦长最短时
截得的弦长最短时 的值以及最短弦长.
的值以及最短弦长.
 ,直线
,直线 .
.(1)求证:直线
 恒过定点.
恒过定点.(2)直线
 被圆
被圆 截得的弦长最短时
截得的弦长最短时 的值以及最短弦长.
的值以及最短弦长.
您最近一年使用:0次
2024-01-26更新
|
411次组卷
|
2卷引用:湖南省岳阳市华容县2023-2024学年高二上学期期末监测数学试题
6 . 已知动点M与两个定点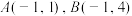 的距离的比为
的距离的比为 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程,并说明其形状;
的方程,并说明其形状;
(2)已知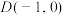 ,过直线
,过直线 上的动点
上的动点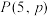 分别作曲线
分别作曲线 的两条切线PQ,
的两条切线PQ, 为切点),连接PD交QR于点
为切点),连接PD交QR于点 ,
,
(ⅰ)证明:直线QR过定点,并求该定点坐标;
(ⅱ)是否存在点P,使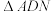 的面积最大?若存在,求出点
的面积最大?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
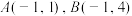 的距离的比为
的距离的比为 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程,并说明其形状;
的方程,并说明其形状;(2)已知
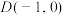 ,过直线
,过直线 上的动点
上的动点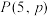 分别作曲线
分别作曲线 的两条切线PQ,
的两条切线PQ, 为切点),连接PD交QR于点
为切点),连接PD交QR于点 ,
,(ⅰ)证明:直线QR过定点,并求该定点坐标;
(ⅱ)是否存在点P,使
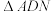 的面积最大?若存在,求出点
的面积最大?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
7 . 设点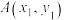
 分别为函数
分别为函数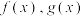 图象上一点,定义
图象上一点,定义 为
为 两点间欧几里得距离,
两点间欧几里得距离,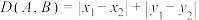 为
为 两点间曼哈顿距离.
两点间曼哈顿距离.
(1)证明 ;
;
(2)设函数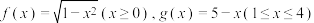 ,求
,求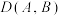 的最小值;
的最小值;
(3)设 为正实数,函数
为正实数,函数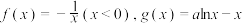 ,对于函数图象上的点
,对于函数图象上的点 有
有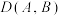 的最小值为4,求
的最小值为4,求 的取值.
的取值.
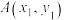
 分别为函数
分别为函数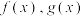 图象上一点,定义
图象上一点,定义 为
为 两点间欧几里得距离,
两点间欧几里得距离,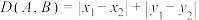 为
为 两点间曼哈顿距离.
两点间曼哈顿距离.(1)证明
 ;
;(2)设函数
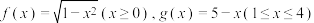 ,求
,求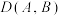 的最小值;
的最小值;(3)设
 为正实数,函数
为正实数,函数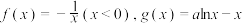 ,对于函数图象上的点
,对于函数图象上的点 有
有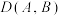 的最小值为4,求
的最小值为4,求 的取值.
的取值.
您最近一年使用:0次
8 . 已知圆 和直线
和直线 .
.
(1)求证:不论 取什么值,直线
取什么值,直线 和圆
和圆 总相交;
总相交;
(2)求直线 被圆
被圆 截得的最短弦长及此时的直线方程.
截得的最短弦长及此时的直线方程.
 和直线
和直线 .
.(1)求证:不论
 取什么值,直线
取什么值,直线 和圆
和圆 总相交;
总相交;(2)求直线
 被圆
被圆 截得的最短弦长及此时的直线方程.
截得的最短弦长及此时的直线方程.
您最近一年使用:0次
2023-05-11更新
|
598次组卷
|
5卷引用:专题2.2 直线与圆的位置关系(2个考点十二大题型)(1)
(已下线)专题2.2 直线与圆的位置关系(2个考点十二大题型)(1)贵州省遵义市第二教育集团2021-2022学年高二上学期期末联考数学(理)试题(已下线)2.5.1 直线与圆的位置关系(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)贵州省遵义市第二教育集团2021-2022学年高二上学期期末联考数学(文)试题(已下线)通关练11 圆的方程大题10考点精练(47题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)
9 . 已知圆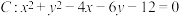 ,直线
,直线 .
.
(1)证明:直线 恒过定点;
恒过定点;
(2)直线 与圆
与圆 交于
交于 两点,当
两点,当 最小时,求直线
最小时,求直线 的方程.
的方程.
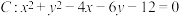 ,直线
,直线 .
.(1)证明:直线
 恒过定点;
恒过定点;(2)直线
 与圆
与圆 交于
交于 两点,当
两点,当 最小时,求直线
最小时,求直线 的方程.
的方程.
您最近一年使用:0次
2024-01-29更新
|
345次组卷
|
2卷引用:河北省张家口市2023-2024学年高二上学期1月期末考试数学试题
解题方法
10 . 已知圆C: 及直线l:
及直线l: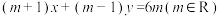 .
.
(1)求证:不论m取什么实数,直线l与圆C总相交;
(2)求直线l被圆C截得的弦长最短长度及此时的直线方程.
 及直线l:
及直线l: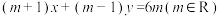 .
.(1)求证:不论m取什么实数,直线l与圆C总相交;
(2)求直线l被圆C截得的弦长最短长度及此时的直线方程.
您最近一年使用:0次



