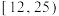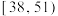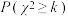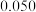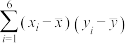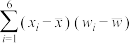名校
1 . 轻食是餐饮的一种形态、轻的不仅仅是食材分量,更是食材烹饪方式简约,保留食材本来的营养和味道,近年来随着消费者健康意识的提升及美颜经济的火热,轻食行业迎来快速发展.某传媒公司为了获得轻食行业消费者行为数据,对中国轻食消费者进行抽样调查.统计其中400名中国轻食消费者(表中4个年龄段的人数各100人)食用轻食的频数与年龄得到如下的频数分布表.
(1)若把年龄在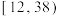 的消费者称为青少年,年龄在
的消费者称为青少年,年龄在 的消费者称为中老年,每周食用轻食的频数不超过3次的称为食用轻食频率低,不低于4次的称为食用轻食频率高,根据所给数据,完成
的消费者称为中老年,每周食用轻食的频数不超过3次的称为食用轻食频率低,不低于4次的称为食用轻食频率高,根据所给数据,完成 列联表,并根据列联表判断是否有99%的把握认为食用轻食频率的高低与年龄有关;
列联表,并根据列联表判断是否有99%的把握认为食用轻食频率的高低与年龄有关;
(2)从每天食用轻食1次及以上的样本消费者中按照表中年龄段采用分层抽样,从中抽取8人,再从这8人中随机抽取3人,记这3人中年龄在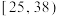 与
与 的人数分别为
的人数分别为 ,
, ,
,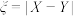 .求
.求 的分布列与期望;
的分布列与期望;
(3)已知小李每天早餐、晚餐都食用轻食,且早餐与晚餐在低卡甜品、全麦夹心吐司、果蔬汁3种轻食中选择一种,已知小李在某天早餐随机选择一种轻食,如果早餐选择低卡甜品、全麦夹心吐司、果蔬汁,则晚餐选择低卡甜品的概率分别为 ,
, ,
, ,求小李晚餐选择低卡甜品的概率.
,求小李晚餐选择低卡甜品的概率.
参考公式: ,
, .
.
附:
使用频数 |
|
|
|
|
偶尔1次 | 30 | 15 | 5 | 10 |
每周1~3次 | 40 | 40 | 30 | 50 |
每周4~6次 | 25 | 40 | 45 | 30 |
每天1次及以上 | 5 | 5 | 20 | 10 |
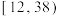 的消费者称为青少年,年龄在
的消费者称为青少年,年龄在 的消费者称为中老年,每周食用轻食的频数不超过3次的称为食用轻食频率低,不低于4次的称为食用轻食频率高,根据所给数据,完成
的消费者称为中老年,每周食用轻食的频数不超过3次的称为食用轻食频率低,不低于4次的称为食用轻食频率高,根据所给数据,完成 列联表,并根据列联表判断是否有99%的把握认为食用轻食频率的高低与年龄有关;
列联表,并根据列联表判断是否有99%的把握认为食用轻食频率的高低与年龄有关;(2)从每天食用轻食1次及以上的样本消费者中按照表中年龄段采用分层抽样,从中抽取8人,再从这8人中随机抽取3人,记这3人中年龄在
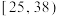 与
与 的人数分别为
的人数分别为 ,
, ,
,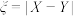 .求
.求 的分布列与期望;
的分布列与期望;(3)已知小李每天早餐、晚餐都食用轻食,且早餐与晚餐在低卡甜品、全麦夹心吐司、果蔬汁3种轻食中选择一种,已知小李在某天早餐随机选择一种轻食,如果早餐选择低卡甜品、全麦夹心吐司、果蔬汁,则晚餐选择低卡甜品的概率分别为
 ,
, ,
, ,求小李晚餐选择低卡甜品的概率.
,求小李晚餐选择低卡甜品的概率.参考公式:
 ,
, .
.附:
| 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-02-29更新
|
735次组卷
|
12卷引用:山东省泰安市泰山外国语学校2024届高三上学期期末数学试题
山东省泰安市泰山外国语学校2024届高三上学期期末数学试题山东省德州市第一中学2024届高三上学期期末数学试题河南省名校学术联盟2024届高三高考模拟信息卷&押题卷数学试题(二)广东省汕头市潮阳实验学校2024届高三上学期第四次阶段测试数学试题四川省德阳市2024届高三下学期质量监测考试(二)数学(理科)试卷(已下线)专题21 概率与统计的综合运用(13大核心考点)(讲义)(已下线)【一题多变】 分类变量 独立检验(已下线)专题05 成对数据的统计分析压轴题(2)(已下线)8.3 列联表与独立性检验(分层练习,6大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)8.3.2 独立性检验——课后作业(巩固版)(已下线)专题8.6 成对数据的统计分析全章八大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
名校
2 . 为了开展“成功源自习惯,习惯来自日常”主题班会活动,引导学生养成良好的行为习惯,提高学习积极性和主动性,在全校学生中随机调查了 名学生的某年度综合评价学习成绩,研究学习成绩是否与行为习惯有关.已知在全部
名学生的某年度综合评价学习成绩,研究学习成绩是否与行为习惯有关.已知在全部 人中随机抽取一人,抽到行为习惯良好的概率为
人中随机抽取一人,抽到行为习惯良好的概率为 ,现按“行为习惯良好”和“行为习惯不够良好”分为两组,再将两组学生的学习成绩分成五组:
,现按“行为习惯良好”和“行为习惯不够良好”分为两组,再将两组学生的学习成绩分成五组: 、
、 、
、 、
、 、
、 ,绘制得到如图所示的频率分布直方图.
,绘制得到如图所示的频率分布直方图. 分为“学习标兵”,请你根据已知条件填写下列
分为“学习标兵”,请你根据已知条件填写下列 列联表,并判断是否有
列联表,并判断是否有 的把握认为“学习标兵与行为习惯是否良好有关”;
的把握认为“学习标兵与行为习惯是否良好有关”;
(2)现从样本中学习成绩低于 分的学生中随机抽取
分的学生中随机抽取 人,记抽到的学生中“行为习惯不够良好”的人数为
人,记抽到的学生中“行为习惯不够良好”的人数为 ,求
,求 的分布列和期望.
的分布列和期望.
参考公式与数据: ,其中
,其中 .
.
 名学生的某年度综合评价学习成绩,研究学习成绩是否与行为习惯有关.已知在全部
名学生的某年度综合评价学习成绩,研究学习成绩是否与行为习惯有关.已知在全部 人中随机抽取一人,抽到行为习惯良好的概率为
人中随机抽取一人,抽到行为习惯良好的概率为 ,现按“行为习惯良好”和“行为习惯不够良好”分为两组,再将两组学生的学习成绩分成五组:
,现按“行为习惯良好”和“行为习惯不够良好”分为两组,再将两组学生的学习成绩分成五组: 、
、 、
、 、
、 、
、 ,绘制得到如图所示的频率分布直方图.
,绘制得到如图所示的频率分布直方图.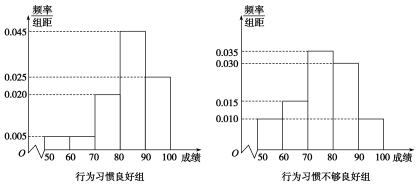
 分为“学习标兵”,请你根据已知条件填写下列
分为“学习标兵”,请你根据已知条件填写下列 列联表,并判断是否有
列联表,并判断是否有 的把握认为“学习标兵与行为习惯是否良好有关”;
的把握认为“学习标兵与行为习惯是否良好有关”;行为习惯良好 | 行为习惯不够良好 | 总计 | |
学习标兵 | |||
非学习标兵 | |||
总计 |
 分的学生中随机抽取
分的学生中随机抽取 人,记抽到的学生中“行为习惯不够良好”的人数为
人,记抽到的学生中“行为习惯不够良好”的人数为 ,求
,求 的分布列和期望.
的分布列和期望.参考公式与数据:
 ,其中
,其中 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
您最近一年使用:0次
2024-02-28更新
|
586次组卷
|
6卷引用:山东省德州市2024届高三下学期开学考试数学试题
山东省德州市2024届高三下学期开学考试数学试题湖南师范大学附属中学(思沁校区)2023-2024学年高三下学期3月月考数学试题(已下线)8.3 列联表与独立性检验(分层练习,6大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)辽宁省沈阳市辽宁实验中学北校2023-2024学年高二下学期4月阶段测试数学试题(已下线)8.3.2 独立性检验——课后作业(提升版)(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
名校
3 . 某市为繁荣地方经济,大力实行人才引进政策,为了解政策的效果,统计了2018-2023年人才引进的数量 (单位:万人),并根据统计数据绘制了如图所示的散点图(
(单位:万人),并根据统计数据绘制了如图所示的散点图( 表示年份代码,年份代码1-6分别代表2018-2023年).
表示年份代码,年份代码1-6分别代表2018-2023年).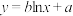 与
与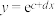 (
(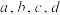 均为常数)哪一个适合作为
均为常数)哪一个适合作为 关于
关于 的回归方程类型;(给出结论即可,不必说明理由)
的回归方程类型;(给出结论即可,不必说明理由)
(2)根据(1)的结果及表中的数据,求出 关于
关于 的回归方程,并预测该市2025年引进人才的数量;
的回归方程,并预测该市2025年引进人才的数量;
(3)从这6年中随机抽取4年,记引进人才数量超过4万人的年数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
参考数据:
其中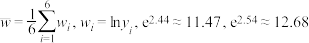 .
.
参考公式:对于一组数据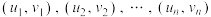 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: .
.
 (单位:万人),并根据统计数据绘制了如图所示的散点图(
(单位:万人),并根据统计数据绘制了如图所示的散点图( 表示年份代码,年份代码1-6分别代表2018-2023年).
表示年份代码,年份代码1-6分别代表2018-2023年).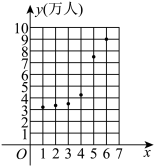
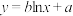 与
与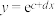 (
(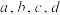 均为常数)哪一个适合作为
均为常数)哪一个适合作为 关于
关于 的回归方程类型;(给出结论即可,不必说明理由)
的回归方程类型;(给出结论即可,不必说明理由)(2)根据(1)的结果及表中的数据,求出
 关于
关于 的回归方程,并预测该市2025年引进人才的数量;
的回归方程,并预测该市2025年引进人才的数量;(3)从这6年中随机抽取4年,记引进人才数量超过4万人的年数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.参考数据:
|
|
|
|
|
5.15 | 1.55 | 17.5 | 20.95 | 3.85 |
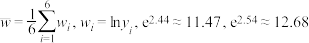 .
.参考公式:对于一组数据
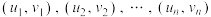 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: .
.
您最近一年使用:0次
2024-02-23更新
|
896次组卷
|
6卷引用:山东省齐鲁名校联盟2024届高三下学期开学质量检测数学试题
山东省齐鲁名校联盟2024届高三下学期开学质量检测数学试题山东省菏泽市第三中学2024届高三下学期3月月考数学试题(已下线)专题8.2 一元线性回归模型及其应用【七大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第八章:成对数据的统计分析章末重点题型复习(5题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题8.6 成对数据的统计分析全章八大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
23-24高三上·山东德州·期末
名校
4 . 某市号召市民尽量减少开车出行,以绿色低碳的出行方式支持节能减排.原来天天开车上班的王先生积极响应政府号召,准备每天在骑自行车和开车两种出行方式中随机选择一种方式出行.从即日起出行方式选择规则如下:第一天选择骑自行车方式上班,随后每天用“一次性抛掷4枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于3,则该天出行方式与前一天相同,否则选择另一种出行方式.
(1)设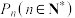 表示事件“在第
表示事件“在第 天,王先生上班选择的是骑自行车出行方式”的概率.
天,王先生上班选择的是骑自行车出行方式”的概率.
①求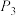 ;
;
②用 表示
表示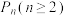 ;
;
(2)依据 值,阐述说明王先生的这种随机选择出行方式是否积极响应市政府的号召.
值,阐述说明王先生的这种随机选择出行方式是否积极响应市政府的号召.
(1)设
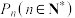 表示事件“在第
表示事件“在第 天,王先生上班选择的是骑自行车出行方式”的概率.
天,王先生上班选择的是骑自行车出行方式”的概率.①求
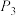 ;
;②用
 表示
表示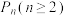 ;
;(2)依据
 值,阐述说明王先生的这种随机选择出行方式是否积极响应市政府的号召.
值,阐述说明王先生的这种随机选择出行方式是否积极响应市政府的号召.
您最近一年使用:0次
名校
5 . 为检验预防某种疾病的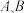 两种疫苗的免疫效果,随机抽取接种
两种疫苗的免疫效果,随机抽取接种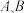 疫苗的志愿者各100名,化验其血液中某项医学指标(该医学指标范围为
疫苗的志愿者各100名,化验其血液中某项医学指标(该医学指标范围为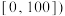 ,统计如下:
,统计如下:
个别数据模糊不清,用含字母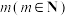 的代数式表示.
的代数式表示.
(1)为检验该项医学指标在 内的是否需要接种加强针,先从医学指标在
内的是否需要接种加强针,先从医学指标在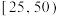 的志愿者中,按接种
的志愿者中,按接种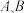 疫苗分层抽取8人,再次抽血化验进行判断.从这8人中随机抽取4人调研医学指标低的原因,记这4人中接种
疫苗分层抽取8人,再次抽血化验进行判断.从这8人中随机抽取4人调研医学指标低的原因,记这4人中接种 疫苗的人数为
疫苗的人数为 ,求
,求 的分布列与数学期望;
的分布列与数学期望;
(2)根据(1)化验研判结果,医学认为该项医学指标低于50,产生抗体较弱,需接种加强针,该项医学指标不低于50,产生抗体较强,不需接种加强针.请先完成下面的 列联表,若根据小概率
列联表,若根据小概率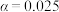 的独立性检验,认为接种
的独立性检验,认为接种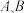 疫苗与志愿者产生抗体的强弱有关联,求
疫苗与志愿者产生抗体的强弱有关联,求 的最大值.
的最大值.
附: ,其中
,其中 .
.
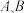 两种疫苗的免疫效果,随机抽取接种
两种疫苗的免疫效果,随机抽取接种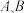 疫苗的志愿者各100名,化验其血液中某项医学指标(该医学指标范围为
疫苗的志愿者各100名,化验其血液中某项医学指标(该医学指标范围为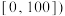 ,统计如下:
,统计如下:| 该项医学指标 | 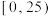 | 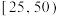 | 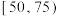 | 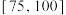 |
接种 疫苗人数 疫苗人数 |  | 10 | 50 |  |
接种 疫苗人数 疫苗人数 |  | 30 | 40 | 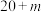 |
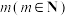 的代数式表示.
的代数式表示.(1)为检验该项医学指标在
 内的是否需要接种加强针,先从医学指标在
内的是否需要接种加强针,先从医学指标在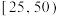 的志愿者中,按接种
的志愿者中,按接种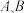 疫苗分层抽取8人,再次抽血化验进行判断.从这8人中随机抽取4人调研医学指标低的原因,记这4人中接种
疫苗分层抽取8人,再次抽血化验进行判断.从这8人中随机抽取4人调研医学指标低的原因,记这4人中接种 疫苗的人数为
疫苗的人数为 ,求
,求 的分布列与数学期望;
的分布列与数学期望;(2)根据(1)化验研判结果,医学认为该项医学指标低于50,产生抗体较弱,需接种加强针,该项医学指标不低于50,产生抗体较强,不需接种加强针.请先完成下面的
 列联表,若根据小概率
列联表,若根据小概率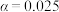 的独立性检验,认为接种
的独立性检验,认为接种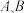 疫苗与志愿者产生抗体的强弱有关联,求
疫苗与志愿者产生抗体的强弱有关联,求 的最大值.
的最大值.| 疫苗 | 抗体 | 合计 | |
| 抗体弱 | 抗体强 | ||
 疫苗 疫苗 | |||
 疫苗 疫苗 | |||
| 合计 | |||
 ,其中
,其中 .
. | 0.25 | 0.025 | 0.005 |
 | 1.323 | 5.024 | 7.879 |
您最近一年使用:0次
2024-01-15更新
|
818次组卷
|
4卷引用:山东省青岛市第二中学2024届高三上学期期末数学试题
山东省青岛市第二中学2024届高三上学期期末数学试题湖南省长沙市湖南师大附中2024届高三上学期月考数学试题(五)(已下线)第03讲 8.3 列联表与独立性检验(知识清单+5类热点题型精讲+强化分层精练)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)8.3.2 独立性检验——课后作业(巩固版)
解题方法
6 . 某中学的风筝兴趣小组决定举行一次盲盒风筝比赛,比赛采取得分制度评选优胜者,可选择的风筝为硬翅风筝、软翅风筝、串式风筝、板式风筝、立体风筝,共有5种风筝,将风筝装入盲盒中摸取风筝,每位参赛选手摸取硬翅风筝或软翅风筝均得1分并放飞风筝,摸取串式风筝、板式风筝、立体风筝均得2分并放飞风筝,每次摸取风筝的结果相互独立,且每次只能摸取1只风筝,每位选手每次摸取硬翅风筝或软翅风筝的概率为 ,摸取其余3种风筝的概率为
,摸取其余3种风筝的概率为 .
.
(1)若选手甲连续摸了2次盲盒,其总得分为 分,求
分,求 的分布列与期望;
的分布列与期望;
(2)假设选手乙可持续摸取盲盒,即摸取盲盒的次数可以为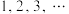 中的任意一个数,记乙累计得
中的任意一个数,记乙累计得 分的概率为
分的概率为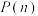 ,当
,当 时,求
时,求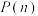 .
.
 ,摸取其余3种风筝的概率为
,摸取其余3种风筝的概率为 .
.(1)若选手甲连续摸了2次盲盒,其总得分为
 分,求
分,求 的分布列与期望;
的分布列与期望;(2)假设选手乙可持续摸取盲盒,即摸取盲盒的次数可以为
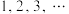 中的任意一个数,记乙累计得
中的任意一个数,记乙累计得 分的概率为
分的概率为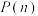 ,当
,当 时,求
时,求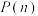 .
.
您最近一年使用:0次
2023-12-22更新
|
1362次组卷
|
6卷引用:山东省潍坊市安丘市青云学府2024届高三上学期期末适应性考试数学试题
山东省潍坊市安丘市青云学府2024届高三上学期期末适应性考试数学试题广东省部分名校2024届高三上学期联合质量检测数学试题(已下线)考点11 由实际问题探究递推关系 2024届高考数学考点总动员【练】(已下线)第4讲:概率与数列的结合问题【练】(已下线)2024年高考数学全真模拟卷06(新题型地区专用)(已下线)2024届新高考数学信息卷2
名校
7 . 某中学有A,B两个餐厅为老师与学生们提供午餐与晚餐服务,王同学、张老师两人每天午餐和晚餐都在学校就餐,近一个月(30天)选择餐厅就餐情况统计如下:
假设王同学、张老师选择餐厅相互独立,用频率估计概率.
(1)估计一天中王同学午餐和晚餐选择不同餐厅就餐的概率;
(2)记X为王同学、张老师在一天中就餐餐厅的个数,求X的分布列和数学期望 ;
;
(3)假设M表示事件“A餐厅推出优惠套餐”,N表示事件“某学生去A餐厅就餐”,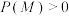 ,已知推出优惠套餐的情况下学生去该餐厅就餐的概率会比不推出优惠套餐的情况下去该餐厅就餐的概率要大,证明.
,已知推出优惠套餐的情况下学生去该餐厅就餐的概率会比不推出优惠套餐的情况下去该餐厅就餐的概率要大,证明. .
.
| 选择餐厅情况(午餐,晚餐) | 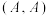 | 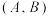 | 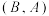 | 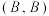 |
| 王同学 | 9天 | 6天 | 12天 | 3天 |
| 张老师 | 6天 | 6天 | 6天 | 12天 |
(1)估计一天中王同学午餐和晚餐选择不同餐厅就餐的概率;
(2)记X为王同学、张老师在一天中就餐餐厅的个数,求X的分布列和数学期望
 ;
;(3)假设M表示事件“A餐厅推出优惠套餐”,N表示事件“某学生去A餐厅就餐”,
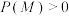 ,已知推出优惠套餐的情况下学生去该餐厅就餐的概率会比不推出优惠套餐的情况下去该餐厅就餐的概率要大,证明.
,已知推出优惠套餐的情况下学生去该餐厅就餐的概率会比不推出优惠套餐的情况下去该餐厅就餐的概率要大,证明. .
.
您最近一年使用:0次
2023-12-14更新
|
1656次组卷
|
8卷引用:山东省济南市山东省实验中学2024届高三上学期第三次诊断考试数学试题
山东省济南市山东省实验中学2024届高三上学期第三次诊断考试数学试题(已下线)模块六 全真模拟篇 拔高2 期末终极研习室(2023-2024学年第一学期)高三江苏省扬州市广陵区红桥高级中学 2024届高三上学期12月月考数学试题山西省运城市盐湖区第五高级中学2024届高三上学期一轮复习成果检测数学试题广东省珠海市第一中学2024届高三上学期期末模拟数学试题(三)(已下线)第01讲 7.1.1条件概率-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)7.1.1 条件概率——课后作业(提升版)(已下线)专题07 概率与统计综合问题(6类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)
2023高三上·全国·专题练习
名校
8 . 数独是源自18世纪瑞士的一种数学游戏,玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(3×3)内的数字均含1~9,且不重复.数独爱好者小明打算报名参加“丝路杯”全国数独大赛初级组的比赛.
参考数据 :
:
参考公式:对于一组数据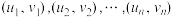 ,其经验回归方程
,其经验回归方程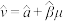 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为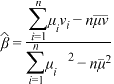 ,
,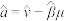 .
.
(1)赛前小明进行了一段时间的训练,每天解题的平均速度y(秒/题)与训练天数x(天)有关,经统计得到如下数据:
现用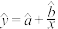 作为回归方程模型,请利用表中数据,求出该回归方程;(
作为回归方程模型,请利用表中数据,求出该回归方程;( ,
,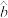 用分数表示)
用分数表示)
(2)小明和小红玩“对战赛”,每局两人同时开始解一道数独题,先解出题的人获胜,不存在平局,两人约定先胜3局者赢得比赛.若小明每局获胜的概率为 ,且各局之间相互独立,设比赛X局后结束,求随机变量X的分布列及均值.
,且各局之间相互独立,设比赛X局后结束,求随机变量X的分布列及均值.
参考数据
 :
: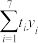 | 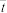 | 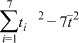 |
| 1 750 | 0.37 | 0.55 |
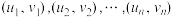 ,其经验回归方程
,其经验回归方程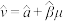 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为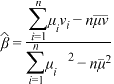 ,
,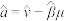 .
.(1)赛前小明进行了一段时间的训练,每天解题的平均速度y(秒/题)与训练天数x(天)有关,经统计得到如下数据:
| x(天) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y(秒/题) | 910 | 800 | 600 | 440 | 300 | 240 | 210 |
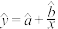 作为回归方程模型,请利用表中数据,求出该回归方程;(
作为回归方程模型,请利用表中数据,求出该回归方程;( ,
,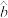 用分数表示)
用分数表示)(2)小明和小红玩“对战赛”,每局两人同时开始解一道数独题,先解出题的人获胜,不存在平局,两人约定先胜3局者赢得比赛.若小明每局获胜的概率为
 ,且各局之间相互独立,设比赛X局后结束,求随机变量X的分布列及均值.
,且各局之间相互独立,设比赛X局后结束,求随机变量X的分布列及均值.
您最近一年使用:0次
2023-12-08更新
|
1276次组卷
|
8卷引用:山东省潍坊市昌乐第一中学2024届高三上学期12月月考数学试题
山东省潍坊市昌乐第一中学2024届高三上学期12月月考数学试题(已下线)第九章 重难专攻(十二)概率中的综合题 核心考点集训 一轮点点通(已下线)专题21 概率与统计的综合运用(13大题型)(练习)(已下线)4.3.1 一元线性回归模型线(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第二册)(已下线)第04讲 拓展一:数学建模 建立统计模型进行预测(非线性回归模型)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)9.1 线性回归分析(2)内蒙古呼和浩特市回民区2023-2024学年高二下学期期中考试数学试题
名校
解题方法
9 . 法国数学家庞加莱是个喜欢吃面包的人,他每天都会到同一家面包店购买一个面包.该面包店的面包师声称自己所出售的面包的平均质量是1 000 g,上下浮动不超过50 g.这句话用数学语言来表达就是:每个面包的质量服从期望为1 000 g,标准差为50 g的正态分布.
(1)已知如下结论:若X~N(μ,σ2),从X的取值中随机抽取k(k∈N*,k≥2)个数据,记这k个数据的平均值为Y,则随机变量Y~N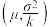 .利用该结论解决下面问题.
.利用该结论解决下面问题.
①假设面包师的说法是真实的,随机购买25个面包,记随机购买25个面包的平均值为Y,求P(Y≤980);
②庞加莱每天都会将买来的面包称重并记录,25天后,得到的数据都落在区间(950,1 050)内,并得出计算25个面包的平均质量为978.72 g.庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有6个面包,其中黑色面包2个;第二箱中共装有8个面包,其中黑色面包3个.现随机挑选一箱,然后从该箱中随机取出2个面包,求取出黑色面包个数的分布列及数学期望.
附:①若随机变量η服从正态分布N(μ,σ2),则P(μ-σ≤η≤μ+σ)≈0.682 7,P(μ-2σ≤η≤μ+2σ)≈0.954 5,P(μ-3σ≤η≤μ+3σ)≈0.997 3;②通常把发生概率小于0.05的事件称为小概率事件,小概率事件基本不会发生.
(1)已知如下结论:若X~N(μ,σ2),从X的取值中随机抽取k(k∈N*,k≥2)个数据,记这k个数据的平均值为Y,则随机变量Y~N
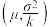 .利用该结论解决下面问题.
.利用该结论解决下面问题.①假设面包师的说法是真实的,随机购买25个面包,记随机购买25个面包的平均值为Y,求P(Y≤980);
②庞加莱每天都会将买来的面包称重并记录,25天后,得到的数据都落在区间(950,1 050)内,并得出计算25个面包的平均质量为978.72 g.庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有6个面包,其中黑色面包2个;第二箱中共装有8个面包,其中黑色面包3个.现随机挑选一箱,然后从该箱中随机取出2个面包,求取出黑色面包个数的分布列及数学期望.
附:①若随机变量η服从正态分布N(μ,σ2),则P(μ-σ≤η≤μ+σ)≈0.682 7,P(μ-2σ≤η≤μ+2σ)≈0.954 5,P(μ-3σ≤η≤μ+3σ)≈0.997 3;②通常把发生概率小于0.05的事件称为小概率事件,小概率事件基本不会发生.
您最近一年使用:0次
2024-03-21更新
|
398次组卷
|
21卷引用:山东省青岛市四区2021-2022学年高三上学期期末考试数学试题
山东省青岛市四区2021-2022学年高三上学期期末考试数学试题山东省青岛市4区县2021-2022学年高三上学期期末考试数学试题湖南省长沙市雅礼中学2022-2023学年高三上学期月考(五)数学试题浙江省杭州第二中学2023届高三下学期3月月考数学试题江苏省扬州中学2023届高三下学期阶段测试数学试题江苏省盐城市伍佑中学2023届高三高考热身考试数学试题辽宁省大连市第八中学2023届高考适应性测试数学试题福建省厦门第一中学2023届高三二模数学试题辽宁省锦州市某校2023-2024学年高三上学期第二次考试数学试题(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-3福建省尤溪第一中学2021~2022学年高二下学期数学期末模拟卷(三)试题江苏省常州市溧阳中学2022-2023学年高二下学期4月阶段性调研测试数学试题河北省保定市六校联盟2022-2023学年高二下学期4月联考数学试题(已下线)8.3 正态分布-【题型分类归纳】2022-2023学年高二数学同步讲与练(苏教版2019选择性必修第二册)(已下线)专题04 超几何分布+二项分布+正态分布压轴题(3)(已下线)第八章 概率(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第8章 概率单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第七章:随机变量及其分布章末重点题型复习-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)黑龙江省牡丹江市第一高级中学2023-2024学年高二下学期5月期中考试数学试题(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)
名校
10 . 某中学高三年级为丰富学生课余生活,减轻学习压力,组建了篮球社团.为了了解学生喜欢篮球是否与性别有关,随机抽取了该年级男、女同学各50名进行调查,部分数据如表所示:
附:
(1)根据所给数据完成上表,依据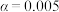 的独立性检验,能否有
的独立性检验,能否有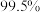 的把握认为该校高三年级学生喜欢篮球与性别有关?
的把握认为该校高三年级学生喜欢篮球与性别有关?
(2)社团指导老师从喜欢篮球的学生中抽取了2名男生和1名女生示范罚分线处定点投篮.已知这两名男生进球的概率均为 ,这名女生进球的概率为
,这名女生进球的概率为 ,每人投篮一次,假设各人进球相互独立,求3人进球总次数
,每人投篮一次,假设各人进球相互独立,求3人进球总次数 的分布列和数学期望.
的分布列和数学期望.
喜欢篮球 | 不喜欢篮球 | 合计 | |
男生 | 20 | ||
女生 | 15 | ||
合计 |

| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
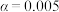 的独立性检验,能否有
的独立性检验,能否有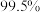 的把握认为该校高三年级学生喜欢篮球与性别有关?
的把握认为该校高三年级学生喜欢篮球与性别有关?(2)社团指导老师从喜欢篮球的学生中抽取了2名男生和1名女生示范罚分线处定点投篮.已知这两名男生进球的概率均为
 ,这名女生进球的概率为
,这名女生进球的概率为 ,每人投篮一次,假设各人进球相互独立,求3人进球总次数
,每人投篮一次,假设各人进球相互独立,求3人进球总次数 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
2023-10-13更新
|
412次组卷
|
2卷引用:山东省临沂市费县2024届高三下学期开学考试数学试题