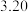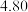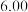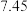名校
解题方法
1 . 某自然保护区经过几十年的发展,某种濒临灭绝动物数量有大幅度的增加.已知这种动物 拥有两个亚种(分别记为
拥有两个亚种(分别记为 种和
种和 种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物
种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物 ,统计其中
,统计其中 种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第
种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第 次试验中
次试验中 种的数目为随机变量
种的数目为随机变量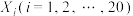 .设该区域中
.设该区域中 种的数目为
种的数目为 ,
, 种的数目为
种的数目为 (
( ,
, 均大于100),每一次试验均相互独立.
均大于100),每一次试验均相互独立.
(1)求 的分布列;
的分布列;
(2)记随机变量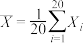 .已知
.已知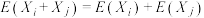 ,
,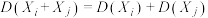
(i)证明: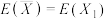 ,
,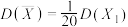 ;
;
(ii)该小组完成所有试验后,得到 的实际取值分别为
的实际取值分别为 .数据
.数据 的平均值
的平均值 ,方差
,方差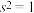 .采用
.采用 和
和 分别代替
分别代替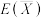 和
和 ,给出
,给出 ,
, 的估计值.
的估计值.
(已知随机变量 服从超几何分布记为:
服从超几何分布记为: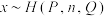 (其中
(其中 为总数,
为总数, 为某类元素的个数,
为某类元素的个数, 为抽取的个数),则
为抽取的个数),则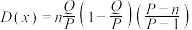 )
)
 拥有两个亚种(分别记为
拥有两个亚种(分别记为 种和
种和 种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物
种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物 ,统计其中
,统计其中 种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第
种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第 次试验中
次试验中 种的数目为随机变量
种的数目为随机变量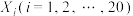 .设该区域中
.设该区域中 种的数目为
种的数目为 ,
, 种的数目为
种的数目为 (
( ,
, 均大于100),每一次试验均相互独立.
均大于100),每一次试验均相互独立.(1)求
 的分布列;
的分布列;(2)记随机变量
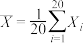 .已知
.已知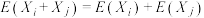 ,
,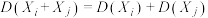
(i)证明:
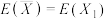 ,
,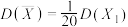 ;
;(ii)该小组完成所有试验后,得到
 的实际取值分别为
的实际取值分别为 .数据
.数据 的平均值
的平均值 ,方差
,方差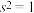 .采用
.采用 和
和 分别代替
分别代替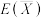 和
和 ,给出
,给出 ,
, 的估计值.
的估计值.(已知随机变量
 服从超几何分布记为:
服从超几何分布记为: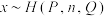 (其中
(其中 为总数,
为总数, 为某类元素的个数,
为某类元素的个数, 为抽取的个数),则
为抽取的个数),则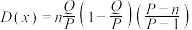 )
)
您最近一年使用:0次
名校
解题方法
2 . 小明从4双鞋中,随机一次取出2只,
(1)求取出的2只鞋都不来自同一双的概率;
(2)若这4双鞋中,恰有一双是小明的,记取出的2只鞋中含有小明的鞋的个数为X,求X的分布列及数学期望 ,
,
(1)求取出的2只鞋都不来自同一双的概率;
(2)若这4双鞋中,恰有一双是小明的,记取出的2只鞋中含有小明的鞋的个数为X,求X的分布列及数学期望
 ,
,
您最近一年使用:0次
2024-05-02更新
|
1662次组卷
|
2卷引用:辽宁省部分学校2024届高三第二次联考(二模)数学试题
名校
3 . 盒中有10个灯泡,其中有三个是坏的,现从盒中随机抽取4个,那么概率是 的事件为( )
的事件为( )
 的事件为( )
的事件为( )| A.恰有1个是坏的 | B.4个全是好的 | C.恰有2个是坏的 | D.至多有2个是坏的 |
您最近一年使用:0次
4 . 甲进行摸球跳格游戏.图上标有第1格,第2格, ,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第
,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第 格的概率为
格的概率为 .
.
(1)甲在一次摸球中摸出红球的个数记为 ,求
,求 的分布列和期望;
的分布列和期望;
(2)证明:数列 为等比数列,并求
为等比数列,并求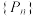 的通项公式.
的通项公式.
 ,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第
,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第 格的概率为
格的概率为 .
.(1)甲在一次摸球中摸出红球的个数记为
 ,求
,求 的分布列和期望;
的分布列和期望;(2)证明:数列
 为等比数列,并求
为等比数列,并求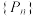 的通项公式.
的通项公式.
您最近一年使用:0次
名校
解题方法
5 . 袋中装有10个大小相同的黑球和白球.已知从袋中任意摸出2个球,至少得到1个白球的概率是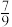 .从袋中任意摸出3个球,记得到白球的个数为
.从袋中任意摸出3个球,记得到白球的个数为 ,求随机变量
,求随机变量 的数学期望
的数学期望______ .
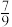 .从袋中任意摸出3个球,记得到白球的个数为
.从袋中任意摸出3个球,记得到白球的个数为 ,求随机变量
,求随机变量 的数学期望
的数学期望
您最近一年使用:0次
2024-04-12更新
|
1151次组卷
|
8卷引用:辽宁省大连市第八中学2023-2024学年高二下学期4月月考数学试题
辽宁省大连市第八中学2023-2024学年高二下学期4月月考数学试题沪教版(2020) 一轮复习 堂堂清 第九单元 9.7 常用分布云南省元谋县第一中学2022-2023学年高二下学期5月月考数学试题(已下线)模块一 专题7 区分超几何分布与二项分布问题(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-1(已下线)专题02 分布列与其数字特征的应用-2上海市位育中学2023-2024学年高二下学期3月月考数学试卷(已下线)8.2 离散型随机变量及其分布列(4)
名校
6 . 某企业响应国家“强芯固基”号召,为汇聚科研力量,准备科学合理增加研发资金.为
了解研发资金的投入额x(单位:千万元)对年收入的附加额y(单位:千万元)的影响,对2017年至2023年研发资金的投入额 和年收入的附加额
和年收入的附加额 进行研究,得到相关数据如下:
进行研究,得到相关数据如下:
(1)求y关于x的线性回归方程;
(2)若年收入的附加额与投入额的比值大于 ,则称对应的年份为“优”,从上面的7个年份中任意取3个,记X表示这三个年份为“优”的个数,求X的分布列及数学期望.
,则称对应的年份为“优”,从上面的7个年份中任意取3个,记X表示这三个年份为“优”的个数,求X的分布列及数学期望.
参考数据: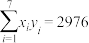 ,
, ,
,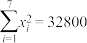 .
.
附:回归方程的斜率和截距的最小二乘估计公式分别为:
 ,
, .
.
了解研发资金的投入额x(单位:千万元)对年收入的附加额y(单位:千万元)的影响,对2017年至2023年研发资金的投入额
 和年收入的附加额
和年收入的附加额 进行研究,得到相关数据如下:
进行研究,得到相关数据如下:年份 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
投入额 | 10 | 30 | 40 | 60 | 80 | 90 | 110 |
年收入的附加额 |
|
|
|
| 7.30 |
|
|
(1)求y关于x的线性回归方程;
(2)若年收入的附加额与投入额的比值大于
 ,则称对应的年份为“优”,从上面的7个年份中任意取3个,记X表示这三个年份为“优”的个数,求X的分布列及数学期望.
,则称对应的年份为“优”,从上面的7个年份中任意取3个,记X表示这三个年份为“优”的个数,求X的分布列及数学期望.参考数据:
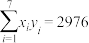 ,
, ,
,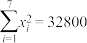 .
.附:回归方程的斜率和截距的最小二乘估计公式分别为:
 ,
, .
.
您最近一年使用:0次
2024-04-08更新
|
1139次组卷
|
2卷引用:辽宁省辽宁省七校协作体2023-2024学年高二下学期5月期中数学试题
名校
7 . 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的20件产品作为样本称出它们的质量(单位:克),质量的分组区间为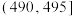 ,
,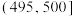 ,…,
,…, .由此得到样本的频率分布直方图(如下图).
.由此得到样本的频率分布直方图(如下图).
(2)在上述抽取的20件产品中任取3件,设 为质量超过505克的产品数量,求
为质量超过505克的产品数量,求 的分布列;
的分布列;
(3)从该流水线上任取5件产品,设 为质量超过505克的产品数量,求
为质量超过505克的产品数量,求 的数学期望和方差.
的数学期望和方差.
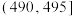 ,
,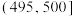 ,…,
,…, .由此得到样本的频率分布直方图(如下图).
.由此得到样本的频率分布直方图(如下图).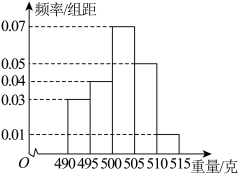
(2)在上述抽取的20件产品中任取3件,设
 为质量超过505克的产品数量,求
为质量超过505克的产品数量,求 的分布列;
的分布列;(3)从该流水线上任取5件产品,设
 为质量超过505克的产品数量,求
为质量超过505克的产品数量,求 的数学期望和方差.
的数学期望和方差.
您最近一年使用:0次
2024-03-21更新
|
1500次组卷
|
5卷引用:辽宁省新高考联盟(点石联考)2023-22024学年高二下学期3月阶段测试数学试题
辽宁省新高考联盟(点石联考)2023-22024学年高二下学期3月阶段测试数学试题(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第七章 随机变量及其分布总结 第二课 提炼本章思想(已下线)专题3.3二项分布与超几何分布(六个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)(已下线)第七章:随机变量及其分布章末重点题型复习(7题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)
名校
8 . 为了开展“成功源自习惯,习惯来自日常”主题班会活动,引导学生养成良好的行为习惯,提高学习积极性和主动性,在全校学生中随机调查了 名学生的某年度综合评价学习成绩,研究学习成绩是否与行为习惯有关.已知在全部
名学生的某年度综合评价学习成绩,研究学习成绩是否与行为习惯有关.已知在全部 人中随机抽取一人,抽到行为习惯良好的概率为
人中随机抽取一人,抽到行为习惯良好的概率为 ,现按“行为习惯良好”和“行为习惯不够良好”分为两组,再将两组学生的学习成绩分成五组:
,现按“行为习惯良好”和“行为习惯不够良好”分为两组,再将两组学生的学习成绩分成五组: 、
、 、
、 、
、 、
、 ,绘制得到如图所示的频率分布直方图.
,绘制得到如图所示的频率分布直方图. 分为“学习标兵”,请你根据已知条件填写下列
分为“学习标兵”,请你根据已知条件填写下列 列联表,并判断是否有
列联表,并判断是否有 的把握认为“学习标兵与行为习惯是否良好有关”;
的把握认为“学习标兵与行为习惯是否良好有关”;
(2)现从样本中学习成绩低于 分的学生中随机抽取
分的学生中随机抽取 人,记抽到的学生中“行为习惯不够良好”的人数为
人,记抽到的学生中“行为习惯不够良好”的人数为 ,求
,求 的分布列和期望.
的分布列和期望.
参考公式与数据: ,其中
,其中 .
.
 名学生的某年度综合评价学习成绩,研究学习成绩是否与行为习惯有关.已知在全部
名学生的某年度综合评价学习成绩,研究学习成绩是否与行为习惯有关.已知在全部 人中随机抽取一人,抽到行为习惯良好的概率为
人中随机抽取一人,抽到行为习惯良好的概率为 ,现按“行为习惯良好”和“行为习惯不够良好”分为两组,再将两组学生的学习成绩分成五组:
,现按“行为习惯良好”和“行为习惯不够良好”分为两组,再将两组学生的学习成绩分成五组: 、
、 、
、 、
、 、
、 ,绘制得到如图所示的频率分布直方图.
,绘制得到如图所示的频率分布直方图.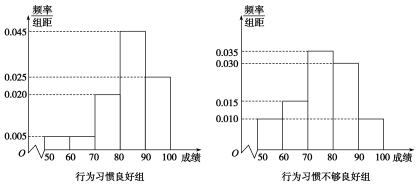
 分为“学习标兵”,请你根据已知条件填写下列
分为“学习标兵”,请你根据已知条件填写下列 列联表,并判断是否有
列联表,并判断是否有 的把握认为“学习标兵与行为习惯是否良好有关”;
的把握认为“学习标兵与行为习惯是否良好有关”;行为习惯良好 | 行为习惯不够良好 | 总计 | |
学习标兵 | |||
非学习标兵 | |||
总计 |
 分的学生中随机抽取
分的学生中随机抽取 人,记抽到的学生中“行为习惯不够良好”的人数为
人,记抽到的学生中“行为习惯不够良好”的人数为 ,求
,求 的分布列和期望.
的分布列和期望.参考公式与数据:
 ,其中
,其中 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
您最近一年使用:0次
2024-02-28更新
|
556次组卷
|
6卷引用:辽宁省沈阳市辽宁实验中学北校2023-2024学年高二下学期4月阶段测试数学试题
辽宁省沈阳市辽宁实验中学北校2023-2024学年高二下学期4月阶段测试数学试题山东省德州市2024届高三下学期开学考试数学试题(已下线)8.3 列联表与独立性检验(分层练习,6大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)湖南师范大学附属中学(思沁校区)2023-2024学年高三下学期3月月考数学试题(已下线)8.3.2 独立性检验——课后作业(提升版)(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
名校
9 . 某班要从3名男同学和5名女同学中随机选出4人去参加某项比赛,设抽取的4人中女同学的人数为 ,则
,则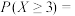
__________ .
 ,则
,则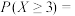
您最近一年使用:0次
2024-01-17更新
|
1114次组卷
|
6卷引用:辽宁省县级重点高中协作体2023-2024学年高二上学期期末数学试题
辽宁省县级重点高中协作体2023-2024学年高二上学期期末数学试题(已下线)专题19 离散型随机变量及其分布列11种常见考法归类(4)(已下线)第07讲 7.4.2超几何分布-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)8.2 离散型随机变量及其分布列(3)(已下线)7.4.2 超几何分布——课后作业(基础版)重庆市第一中学校2023-2024学年高二下学期期中考试数学试题
名校
解题方法
10 . 某企业打算处理一批产品,这些产品每箱10件,以箱为单位销售,已知这批产品中每箱都有废品.每箱的废品率只有 或者
或者 两种可能,且两种可能的产品市场占有率分别为
两种可能,且两种可能的产品市场占有率分别为 .假设该产品正品每件市场价格为100元,废品不值钱,现处理价格为每箱840元,遇到废品不予更换,以一箱产品中正品的价格期望值作为决策依据.(运算结果保留分数)
.假设该产品正品每件市场价格为100元,废品不值钱,现处理价格为每箱840元,遇到废品不予更换,以一箱产品中正品的价格期望值作为决策依据.(运算结果保留分数)
(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,不放回地随机从一箱中抽取2件产品进行检验,已发现在抽取检验的2件产品中,其中恰有一件是废品
①求此箱是废品率为 的概率;
的概率;
②判断此箱是否可以购买,并说明理由.
 或者
或者 两种可能,且两种可能的产品市场占有率分别为
两种可能,且两种可能的产品市场占有率分别为 .假设该产品正品每件市场价格为100元,废品不值钱,现处理价格为每箱840元,遇到废品不予更换,以一箱产品中正品的价格期望值作为决策依据.(运算结果保留分数)
.假设该产品正品每件市场价格为100元,废品不值钱,现处理价格为每箱840元,遇到废品不予更换,以一箱产品中正品的价格期望值作为决策依据.(运算结果保留分数)(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,不放回地随机从一箱中抽取2件产品进行检验,已发现在抽取检验的2件产品中,其中恰有一件是废品
①求此箱是废品率为
 的概率;
的概率;②判断此箱是否可以购买,并说明理由.
您最近一年使用:0次
2024-01-16更新
|
997次组卷
|
4卷引用:辽宁省部分学校2024届高三上学期期末数学试题
辽宁省部分学校2024届高三上学期期末数学试题广东省东莞市东华高级中学2024届高三上学期第二次调研数学试题广东省云浮市云安区云安中学2024届高三下学期开学考试数学试卷(已下线)热点8-2 概率与统计综合(10题型+满分技巧+限时检测)