名校
解题方法
1 . 已知函数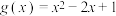 .
.
(1)若存在 ,
,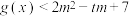 对任意的
对任意的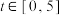 都成立;求m的取值范围;
都成立;求m的取值范围;
(2)设 ,若不等式
,若不等式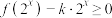 在
在 上有解,求实数k的取值范围.
上有解,求实数k的取值范围.
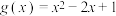 .
.(1)若存在
 ,
,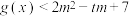 对任意的
对任意的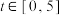 都成立;求m的取值范围;
都成立;求m的取值范围;(2)设
 ,若不等式
,若不等式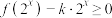 在
在 上有解,求实数k的取值范围.
上有解,求实数k的取值范围.
您最近一年使用:0次
2024-08-31更新
|
778次组卷
|
4卷引用:吉林省长春市第五中学2023-2024学年高二下学期期末考试数学试题
名校
2 . 若定义在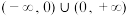 上的函数
上的函数 同时满足;①
同时满足;① 为奇函数;②对任意的
为奇函数;②对任意的 ,
,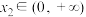 ,且
,且 ,都有
,都有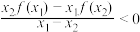 .则称函数
.则称函数 具有性质P.已知函数
具有性质P.已知函数 具有性质P,则不等式
具有性质P,则不等式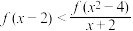 的解集为
的解集为______ .
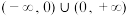 上的函数
上的函数 同时满足;①
同时满足;① 为奇函数;②对任意的
为奇函数;②对任意的 ,
,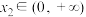 ,且
,且 ,都有
,都有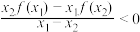 .则称函数
.则称函数 具有性质P.已知函数
具有性质P.已知函数 具有性质P,则不等式
具有性质P,则不等式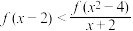 的解集为
的解集为
您最近一年使用:0次
2024-08-29更新
|
669次组卷
|
2卷引用:吉林省长春市十一高中2023-2024学年高一上学期1月期末数学试题
名校
解题方法
3 . 已知函数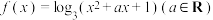 .
.
(1)若 的定义域为
的定义域为 ,求
,求 的取值范围;
的取值范围;
(2)设 ,若对任意
,若对任意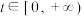 ,函数
,函数 在区间
在区间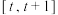 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求 的取值范围.
的取值范围.
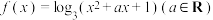 .
.(1)若
 的定义域为
的定义域为 ,求
,求 的取值范围;
的取值范围;(2)设
 ,若对任意
,若对任意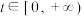 ,函数
,函数 在区间
在区间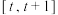 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
4 . 已知函数 的定义域为
的定义域为 ,对任意正实数
,对任意正实数 ,
, 都有
都有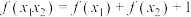 ,且当
,且当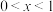 时,
时, .
.
(1)求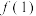 的值;
的值;
(2)试判断 的单调性,并证明;
的单调性,并证明;
(3)若 ,求
,求 的取值范围.
的取值范围.
 的定义域为
的定义域为 ,对任意正实数
,对任意正实数 ,
, 都有
都有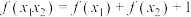 ,且当
,且当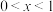 时,
时, .
.(1)求
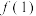 的值;
的值;(2)试判断
 的单调性,并证明;
的单调性,并证明;(3)若
 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-25更新
|
1348次组卷
|
2卷引用:吉林省延边朝鲜族自治州珲春市第一高级中学2023-2024学年高二下学期期末考试数学试题
名校
解题方法
5 . 已知函数 是定义域为
是定义域为 的奇函数,当
的奇函数,当 时,
时,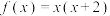 .若
.若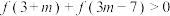 ,则
,则 的取值范围为
的取值范围为_______ .
 是定义域为
是定义域为 的奇函数,当
的奇函数,当 时,
时,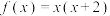 .若
.若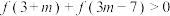 ,则
,则 的取值范围为
的取值范围为
您最近一年使用:0次
2024-07-25更新
|
1330次组卷
|
2卷引用:吉林省延边朝鲜族自治州珲春市第一高级中学2023-2024学年高二下学期期末考试数学试题
名校
6 . 下列说法正确的是( )
A.已知 是奇函数,则有 是奇函数,则有 |
B.函数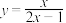 的单调减区间是 的单调减区间是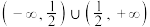 |
C.定义在 上的函数 上的函数 ,若 ,若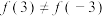 ,则 ,则 不是偶函数 不是偶函数 |
D.已知 在 在 上是增函数,若 上是增函数,若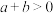 ,则有 ,则有 |
您最近一年使用:0次
2024-07-25更新
|
730次组卷
|
2卷引用:吉林省延边朝鲜族自治州珲春市第一高级中学2023-2024学年高二下学期期末考试数学试题
名校
7 . 已知函数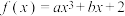 在
在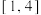 上的值域为
上的值域为 ,则
,则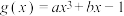 在
在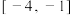 上的值域为( )
上的值域为( )
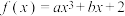 在
在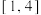 上的值域为
上的值域为 ,则
,则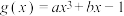 在
在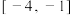 上的值域为( )
上的值域为( )A.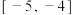 | B.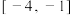 | C. | D.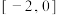 |
您最近一年使用:0次
2024-07-25更新
|
606次组卷
|
2卷引用:吉林省延边朝鲜族自治州珲春市第一高级中学2023-2024学年高二下学期期末考试数学试题
解题方法
8 . 已知函数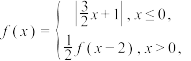 则方程
则方程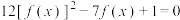 的实数个数为( )
的实数个数为( )
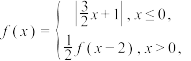 则方程
则方程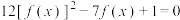 的实数个数为( )
的实数个数为( )| A.9 | B.10 | C.11 | D.12 |
您最近一年使用:0次
2024-07-24更新
|
694次组卷
|
2卷引用:吉林省白山市浑江区盟校2023-2024学年高二下学期7月期末考试数学试题
解题方法
9 . 已知幂函数 (
(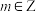 )为偶函数,且在区间
)为偶函数,且在区间 上单调递增,函数
上单调递增,函数 满足
满足 .
.
(1)求函数 和
和 的解析式;
的解析式;
(2)对任意实数 ,
,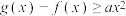 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 (
(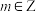 )为偶函数,且在区间
)为偶函数,且在区间 上单调递增,函数
上单调递增,函数 满足
满足 .
.(1)求函数
 和
和 的解析式;
的解析式;(2)对任意实数
 ,
,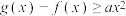 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-24更新
|
475次组卷
|
2卷引用:吉林省白山市浑江区盟校2023-2024学年高二下学期7月期末考试数学试题
名校
10 . 已知函数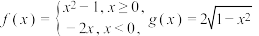 .
.
(1)若 ,求
,求 的取值范围.
的取值范围.
(2)记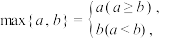 已知函数
已知函数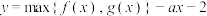 有
有 个不同的零点.
个不同的零点.
①若 ,求
,求 的取值范围;
的取值范围;
②若 ,且
,且 是其中两个非零的零点,求
是其中两个非零的零点,求 的取值范围.
的取值范围.
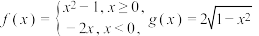 .
.(1)若
 ,求
,求 的取值范围.
的取值范围.(2)记
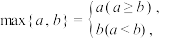 已知函数
已知函数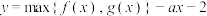 有
有 个不同的零点.
个不同的零点.①若
 ,求
,求 的取值范围;
的取值范围;②若
 ,且
,且 是其中两个非零的零点,求
是其中两个非零的零点,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-24更新
|
378次组卷
|
3卷引用:吉林省吉林市田家炳高级中学2023-2024学年高二下学期7月期末考试数学试题
吉林省吉林市田家炳高级中学2023-2024学年高二下学期7月期末考试数学试题浙江省强基(培优)联盟2023-2024学年高二下学期7月学考联考(期末)数学试题(已下线)周测5 函数图象、函数与方程一轮周测卷(提升卷)



