名校
解题方法
1 . 已知P为棱长为 的正四面体
的正四面体 各面所围成的区域内部(不在表面上)一动点,记P到面
各面所围成的区域内部(不在表面上)一动点,记P到面 ,面
,面 ,面
,面 ,面
,面 的距离分别为
的距离分别为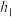 ,
,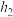 ,
,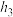 ,
,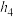 ,若
,若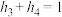 ,则
,则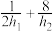 的最小值为( )
的最小值为( )
 的正四面体
的正四面体 各面所围成的区域内部(不在表面上)一动点,记P到面
各面所围成的区域内部(不在表面上)一动点,记P到面 ,面
,面 ,面
,面 ,面
,面 的距离分别为
的距离分别为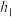 ,
,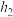 ,
,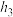 ,
,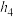 ,若
,若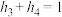 ,则
,则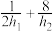 的最小值为( )
的最小值为( )| A.2 | B.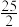 | C.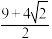 | D.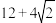 |
您最近一年使用:0次
2024-03-22更新
|
564次组卷
|
5卷引用:河南省五市2024届高三第一次联考数学试题
河南省五市2024届高三第一次联考数学试题(已下线)8.6.2 直线与平面垂直【第三练】“上好三节课,做好三套题“高中数学素养晋级之路广东省广州市第六中学2023-2024学年高二下学期期中考试数学试题(已下线)专题21 空间图形的表面积和体积-《重难点题型·高分突破》(苏教版2019必修第二册)河南省周口市太康县第一高级中学2023-2024学年高一下学期6月月考数学试题
名校
解题方法
2 . 随着北京中轴线申遗工作的进行,古建筑备受关注.故宫不仅是世界上现存规模最大、保存最为完整的木质结构古建筑之一,更是北京中轴线的“中心”.图1是古建筑之首的太和殿,它的重檐庑(wŭ)殿顶可近似看作图2所示的几何体,其中底面 题矩形,
题矩形,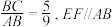 ,四边形
,四边形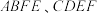 是两个全等的等腰梯形,
是两个全等的等腰梯形, 是两个全等的等腰三角形.若
是两个全等的等腰三角形.若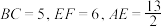 ,则该几何体的体积为( )
,则该几何体的体积为( )
 题矩形,
题矩形,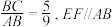 ,四边形
,四边形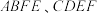 是两个全等的等腰梯形,
是两个全等的等腰梯形, 是两个全等的等腰三角形.若
是两个全等的等腰三角形.若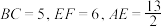 ,则该几何体的体积为( )
,则该几何体的体积为( )
| A.90 | B. | C. | D.135 |
您最近一年使用:0次
2023-11-15更新
|
750次组卷
|
4卷引用:北京市第十三中学2024届高三上学期期中测试数学试题
北京市第十三中学2024届高三上学期期中测试数学试题北京市第二中学2023-2024学年高三下学期开学考试数学试卷(已下线)第1套 重组模拟卷(模块二 2月开学)(已下线)第一节 基本立体图形与几何体【同步课时】北京专项
名校
3 . 在正方体 中,直线
中,直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 平面
平面 ,则直线
,则直线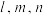 的位置关系可能是( )
的位置关系可能是( )
 中,直线
中,直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 平面
平面 ,则直线
,则直线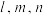 的位置关系可能是( )
的位置关系可能是( )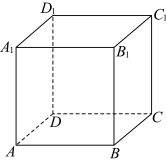
A.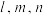 两两垂直 两两垂直 | B.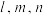 两两平行 两两平行 |
C.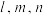 两两相交 两两相交 | D.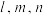 两两异面 两两异面 |
您最近一年使用:0次
2023-11-14更新
|
595次组卷
|
5卷引用:山东省潍坊市2024届高三上学期期中考试数学试题
名校
解题方法
4 . 以下命题中,所有真命题的序号为______
①如果一个角的两边和另一个角的两边分别平行,那么这两个角相等;
②垂直于三角形两边的直线必垂直第三边;
③有两个面互相平行,其余的面都是平行四边形的多面体是棱柱;
④用经过旋转轴的平面截圆锥,所得的截面都是全等的等腰三角形;
①如果一个角的两边和另一个角的两边分别平行,那么这两个角相等;
②垂直于三角形两边的直线必垂直第三边;
③有两个面互相平行,其余的面都是平行四边形的多面体是棱柱;
④用经过旋转轴的平面截圆锥,所得的截面都是全等的等腰三角形;
您最近一年使用:0次
名校
5 . 已知平面 和两直线
和两直线 ,且
,且 . 则添加下列条件中的( ),可以得到结论
. 则添加下列条件中的( ),可以得到结论 .
.
 和两直线
和两直线 ,且
,且 . 则添加下列条件中的( ),可以得到结论
. 则添加下列条件中的( ),可以得到结论 .
.A. | B. | C. | D.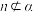 |
您最近一年使用:0次
2023-10-10更新
|
409次组卷
|
4卷引用:北京市海淀区清华志清中学2023-2024学年高二上学期第一次月考练习数学试题
北京市海淀区清华志清中学2023-2024学年高二上学期第一次月考练习数学试题江西省鹰潭市贵溪市第一中学2024届高三上学期期中考试数学试题(已下线)考点9 垂直的判定与性质 2024届高考数学考点总动员(已下线)第一章 点线面位置关系 专题一 空间平行关系的判定与证明 微点1 空间直线平行的判定与证明【基础版】
名校
解题方法
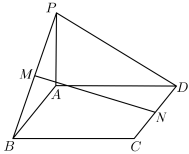
6 . 如图,已知四边形 是矩形,
是矩形, 平面
平面 ,且
,且 ,M、N是线段
,M、N是线段 、
、 上的点,满足
上的点,满足 .
. ,求证:直线
,求证:直线
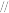 平面
平面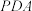 ;
;
(2)是否存在实数 ,使直线
,使直线 同时垂直于直线
同时垂直于直线 ,直线
,直线 ?如果有请求出
?如果有请求出 的值,否则请说明理由;
的值,否则请说明理由;
(3)若 ,求直线
,求直线 与直线
与直线 所成角的最大值.
所成角的最大值.
 是矩形,
是矩形, 平面
平面 ,且
,且 ,M、N是线段
,M、N是线段 、
、 上的点,满足
上的点,满足 .
.
 ,求证:直线
,求证:直线
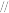 平面
平面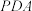 ;
;(2)是否存在实数
 ,使直线
,使直线 同时垂直于直线
同时垂直于直线 ,直线
,直线 ?如果有请求出
?如果有请求出 的值,否则请说明理由;
的值,否则请说明理由;(3)若
 ,求直线
,求直线 与直线
与直线 所成角的最大值.
所成角的最大值.
您最近一年使用:0次
2022-05-07更新
|
453次组卷
|
4卷引用:上海市控江中学2021-2022学年高二下学期期中数学试题
上海市控江中学2021-2022学年高二下学期期中数学试题第10章 空间直线与平面(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(沪教版2020必修第三册)(已下线)10.3 直线与平面所成的角 (第4课时)(作业)(夯实基础+能力提升)-【教材配套课件+作业】2022-2023学年高二数学精品教学课件(沪教版2020必修第三册)【温故练】第10章 空间直线与平面 单元测试-沪教版(2020)必修第三册
名校
7 . 已知平面 满足
满足 ,且
,且 不垂直,直线
不垂直,直线 ,那么下列命题中错误的是( )
,那么下列命题中错误的是( )
 满足
满足 ,且
,且 不垂直,直线
不垂直,直线 ,那么下列命题中错误的是( )
,那么下列命题中错误的是( )A.对任意直线 ,都有 ,都有 | B.存在直线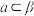 ,使得 ,使得 |
C.存在直线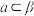 ,使得 ,使得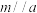 | D.m与平面 一定不垂直 一定不垂直 |
您最近一年使用:0次
2021-11-13更新
|
285次组卷
|
3卷引用:江西省九江市六校2021-2022学年上学期高二期中考试数学(理)试题



