名校
1 . 已知函数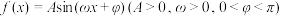 ,其部分图象如图所示,且直线
,其部分图象如图所示,且直线 与曲线
与曲线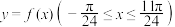 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,下列叙述正确的是( )
,下列叙述正确的是( )
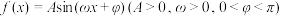 ,其部分图象如图所示,且直线
,其部分图象如图所示,且直线 与曲线
与曲线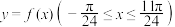 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,下列叙述正确的是( )
,下列叙述正确的是( )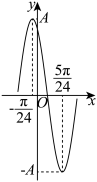
A. |
B.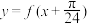 为奇函数 为奇函数 |
C.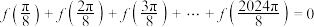 |
D.若 在区间 在区间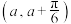 (其中 (其中 )上单调递增,则 )上单调递增,则 的取值范围是 的取值范围是 |
您最近一年使用:0次
名校
解题方法
2 . 下列函数中均满足下面三个条件的是( )
① 为偶函数;②
为偶函数;②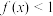 ;③
;③ 有最大值
有最大值
①
 为偶函数;②
为偶函数;②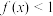 ;③
;③ 有最大值
有最大值A. | B. |
C.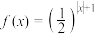 | D. |
您最近一年使用:0次
2024-03-31更新
|
400次组卷
|
2卷引用:安徽省池州市2024届高三上学期期末数学试题
3 . 若 ,则
,则 的可能取值是( )
的可能取值是( )
 ,则
,则 的可能取值是( )
的可能取值是( )A. | B.0 | C.1 | D.2 |
您最近一年使用:0次
解题方法
4 . 把一条线段分割为两部分,使较长部分的长度与全长的比值等于较短与较长部分的长度的比值,这个比值称为黄金分割比(简称黄金比).黄金比在建筑、艺术和科学等领域中都有广泛应用.我们把顶角为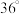 的等腰三角形称为黄金三角形,它满足较短边与较长边的长度之比等于黄金比.由上述信息可求得
的等腰三角形称为黄金三角形,它满足较短边与较长边的长度之比等于黄金比.由上述信息可求得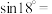
___________ .
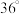 的等腰三角形称为黄金三角形,它满足较短边与较长边的长度之比等于黄金比.由上述信息可求得
的等腰三角形称为黄金三角形,它满足较短边与较长边的长度之比等于黄金比.由上述信息可求得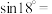
您最近一年使用:0次
名校
5 . 如图所示,已知角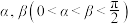 的始边为
的始边为 轴的非负半轴,终边与单位圆的交点分别为
轴的非负半轴,终边与单位圆的交点分别为 ,
, 为线段
为线段 的中点,射线
的中点,射线 与单位圆交于点
与单位圆交于点 ,则( )
,则( )
 的始边为
的始边为 轴的非负半轴,终边与单位圆的交点分别为
轴的非负半轴,终边与单位圆的交点分别为 ,
, 为线段
为线段 的中点,射线
的中点,射线 与单位圆交于点
与单位圆交于点 ,则( )
,则( )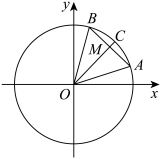
A.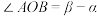 |
B. |
C.点 的坐标为 的坐标为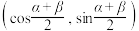 |
D.点 的坐标为 的坐标为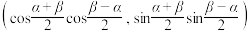 |
您最近一年使用:0次
2024-02-15更新
|
1984次组卷
|
6卷引用:安徽省合肥一六八中学2024届高三“九省联考”考后适应性测试数学试题(三)
安徽省合肥一六八中学2024届高三“九省联考”考后适应性测试数学试题(三)江西省鹰潭市2024届高三第一次模拟考试数学试题山东省济南市2023-2024学年高一上学期1月期末数学试题(已下线)8.2.2两家和与差的正弦、正切-同步精品课堂(人教B版2019必修第三册)(已下线)信息必刷卷05广东省广州市真光中学2023-2024学年高一下学期期中考试数学试卷
名校
解题方法
6 . 已知点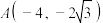 ,
, ,
, ,O为坐标原点,若
,O为坐标原点,若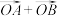 与
与 共线,则
共线,则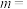 ( )
( )
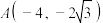 ,
, ,
, ,O为坐标原点,若
,O为坐标原点,若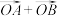 与
与 共线,则
共线,则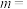 ( )
( )| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
2024-02-14更新
|
592次组卷
|
6卷引用:安徽省部分学校2024届高三上学期期末质量检测数学试题
名校
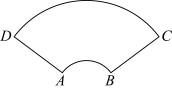
7 . 如图是杭州第19届亚运会的会徽“潮涌”,将其视为一扇面 ,若
,若 的长为
的长为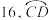 的长为
的长为 ,则扇面
,则扇面 的面积为( )
的面积为( )

 ,若
,若 的长为
的长为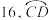 的长为
的长为 ,则扇面
,则扇面 的面积为( )
的面积为( )

| A.190 | B.192 | C.380 | D.384 |
您最近一年使用:0次
2024-01-31更新
|
484次组卷
|
5卷引用:安徽省阜阳市2023-2024学年高一上学期期末联考数学试卷
安徽省阜阳市2023-2024学年高一上学期期末联考数学试卷河南省名校联盟2023-2024学年高一上学期期末数学试题湖北省咸宁市崇阳县第二高级中学2023-2024学年高一下学期寒假检测数学试题(已下线)1.8 三角函数的简单应用4种常见考法归类-【帮课堂】(北师大版2019必修第二册)广东省茂名市高州市第一中学2023-2024学年高一下学期开学考试数学试题
8 . 勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”. 中国是发现和研究勾股定理最古老的国家之一. 据记载,在公元前1120年,商高答周公曰“故折矩,以为勾广三,股修四,径隅五,既方之,外半其一矩,环而共盘,得成三四五,两矩共长二十有五,是谓积矩. ”因此,勾股定理在中国又称“商高定理”. 数百年后,希腊数学家毕达哥拉斯发现并证明了这个定理,因此“勾股定理”在西方被称为“毕达哥拉斯定理”. 三国时期,吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明. 如图所示的勾股圆方图中,四个全等的直角三角形与中间的小正方形拼成一个大正方形. 若中间小正方形面积(阴影部分)是大正方形面积一半,则直角三角形中较小的锐角 的大小为
的大小为_________ .
 的大小为
的大小为
您最近一年使用:0次
名校
解题方法
9 . 如图所示,某小区中心有一块圆心角为 ,半径为
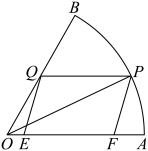
,半径为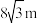 的扇形空地,现计划将该区域设计成亲子室外游乐区域,根据设计要求,需要铺设一块平行四边形的塑胶地面EFPQ(其中点E,F在边OA上,点
的扇形空地,现计划将该区域设计成亲子室外游乐区域,根据设计要求,需要铺设一块平行四边形的塑胶地面EFPQ(其中点E,F在边OA上,点 在边OB上,点
在边OB上,点 在AB上),其他区域地面铺设绿地,设
在AB上),其他区域地面铺设绿地,设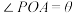 .
. 表示绿地的面积
表示绿地的面积 ;
;
(2)若铺设绿地每平方米100元,要使得铺设绿地的出用 最低,
最低, 应取何值,并求出此时
应取何值,并求出此时 的值.
的值.
 ,半径为
,半径为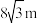 的扇形空地,现计划将该区域设计成亲子室外游乐区域,根据设计要求,需要铺设一块平行四边形的塑胶地面EFPQ(其中点E,F在边OA上,点
的扇形空地,现计划将该区域设计成亲子室外游乐区域,根据设计要求,需要铺设一块平行四边形的塑胶地面EFPQ(其中点E,F在边OA上,点 在边OB上,点
在边OB上,点 在AB上),其他区域地面铺设绿地,设
在AB上),其他区域地面铺设绿地,设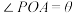 .
.
 表示绿地的面积
表示绿地的面积 ;
;(2)若铺设绿地每平方米100元,要使得铺设绿地的出用
 最低,
最低, 应取何值,并求出此时
应取何值,并求出此时 的值.
的值.
您最近一年使用:0次
2024-01-11更新
|
452次组卷
|
6卷引用:安徽省淮北市树人高级中学2023-2024学年高一上学期期末数学试题
安徽省淮北市树人高级中学2023-2024学年高一上学期期末数学试题河北省沧州市泊头市第一中学2023-2024学年高一上学期1月月考数学试题河南省南阳市方城县第一高级中学2023-2024学年高一上学期期末模拟预测数学试题(已下线)第10章 三角恒等变换章末题型归纳总结-【帮课堂】(苏教版2019必修第二册)(已下线)10.2 二倍角的三角函数 (1)-【帮课堂】(苏教版2019必修第二册)(已下线)1.8 三角函数的简单应用-同步精品课堂(北师大版2019必修第二册)
名校
解题方法
10 . 摩天轮是一种大型转轮状的机械建筑设施,上面挂在轮边缘的是供乘客搭乘的座舱.某地一摩天轮与地面的垂直高度(最高处与地面的距离)为208米,直径193米,入口在最底部.摩天轮逆时针方向匀速转动,30分钟转一圈,假设该摩天轮共有36个座舱,且每两个座舱间隔相等,则下列说法正确的是( )
| A.若摩天轮的转速减半,则其旋转一圈的时间是原来的一半 |
B.乘客从入口进入座舱,摩天轮开始转动后,乘客距离水平地面的高度 米)与时间 米)与时间 (分钟)的函数解析式为 (分钟)的函数解析式为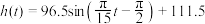 |
| C.乘客从入口进入座舱,摩天轮开始转动后,经过10分钟,乘客距离地面的高度为63.25米 |
| D.游客乙在游客甲后进入座舱,且中间间隔5个座舱,在摩天轮转动一周的过程中,两人距离地面的高度差的最大值为96.5米 |
您最近一年使用:0次
2024-01-11更新
|
486次组卷
|
6卷引用:安徽省淮北市树人高级中学2023-2024学年高一上学期期末数学试题
安徽省淮北市树人高级中学2023-2024学年高一上学期期末数学试题河北省沧州市泊头市第一中学2023-2024学年高一上学期1月月考数学试题(已下线)专题05 三角函数3-2024年高一数学寒假作业单元合订本(已下线)【第三练】5.7三角函数的应用(已下线)考点8 三角函数的实际应用问题 --2024届高考数学考点总动员【练】(已下线)黄金卷05(2024新题型)



