解题方法
1 . 如图,已知 ,
,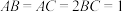 ,且点
,且点 是
是 的重心.过点
的重心.过点 的直线
的直线 与线段
与线段 、
、 分别交于点
分别交于点 、
、 .设
.设 ,
,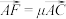 (
(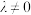 ,
,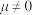 ).
).
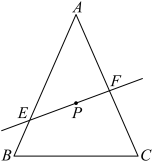
(1)求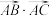 的值,并判断
的值,并判断 是否为定值,若是则求出定值,若不是请说明理由;
是否为定值,若是则求出定值,若不是请说明理由;
(2)若 的周长为
的周长为 ,
, 的周长为
的周长为 .设
.设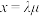 ,记
,记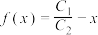 ,求
,求 的取值范围.
的取值范围.
 ,
,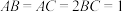 ,且点
,且点 是
是 的重心.过点
的重心.过点 的直线
的直线 与线段
与线段 、
、 分别交于点
分别交于点 、
、 .设
.设 ,
,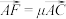 (
(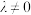 ,
,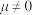 ).
).
(1)求
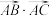 的值,并判断
的值,并判断 是否为定值,若是则求出定值,若不是请说明理由;
是否为定值,若是则求出定值,若不是请说明理由;(2)若
 的周长为
的周长为 ,
, 的周长为
的周长为 .设
.设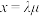 ,记
,记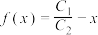 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
2 . 在直角梯形 中,
中,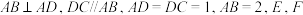 分别为
分别为  的中点,点
的中点,点 在以
在以 为圆心,
为圆心, 为半径的圆弧
为半径的圆弧 上运动(如图所示).若
上运动(如图所示).若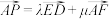 ,其中
,其中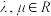 ,则
,则 的取值范围是( )
的取值范围是( )
 中,
中,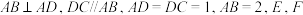 分别为
分别为  的中点,点
的中点,点 在以
在以 为圆心,
为圆心, 为半径的圆弧
为半径的圆弧 上运动(如图所示).若
上运动(如图所示).若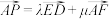 ,其中
,其中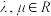 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. |
C.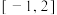 | D.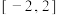 |
您最近一年使用:0次
2024-07-10更新
|
796次组卷
|
3卷引用:四川省成都市石室中学2023-2024学年高一下学期期末考试数学试卷
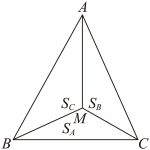
3 . “奔驰定理”因其几何表示酷似奔驰的标志得来,是平面向量中一个非常优美的结论.它的具体内容是:已知 是
是 内一点,
内一点,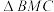 ,
,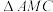 ,
,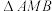 的面积分别为
的面积分别为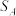 ,
,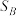 ,
,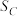 ,且
,且 .若
.若 为
为 的垂心,
的垂心,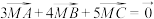 ,则
,则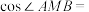 ( )
( )
 是
是 内一点,
内一点,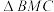 ,
,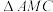 ,
,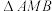 的面积分别为
的面积分别为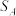 ,
,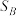 ,
,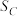 ,且
,且 .若
.若 为
为 的垂心,
的垂心,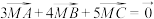 ,则
,则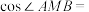 ( )
( )
A.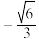 | B.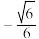 | C.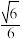 | D. |
您最近一年使用:0次
2024-07-09更新
|
1615次组卷
|
5卷引用:甘肃省2023-2024学年高一下学期期末学业水平质量测试数学试卷
甘肃省2023-2024学年高一下学期期末学业水平质量测试数学试卷(已下线)周测11 平面向量与复数(提升卷)(一轮好卷)辽宁省名校联盟2025届高三上学期10月联考数学试卷(已下线)8.2 平面向量的数量积及应用(讲义)黑龙江省齐齐哈尔市2025届高三10月份考试数学试题
解题方法
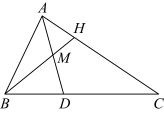
4 . 如图,已知在 中,
中, 是
是 的角平分线,与
的角平分线,与 交于点
交于点 ,
, 是
是 的中点,延长
的中点,延长 交
交 于点
于点 ,
, ,则
,则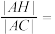
______ .
 中,
中, 是
是 的角平分线,与
的角平分线,与 交于点
交于点 ,
, 是
是 的中点,延长
的中点,延长 交
交 于点
于点 ,
, ,则
,则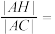
您最近一年使用:0次
2024-07-03更新
|
343次组卷
|
2卷引用:黑龙江省绥化市绥棱县第一中学2023-2024学年高一下学期5月期中考试数学试题
5 . 已知向量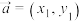 ,
,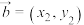 ,定义运算
,定义运算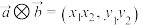 ,同时定义
,同时定义 .
.
(1)若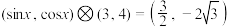 ,求实数
,求实数 的取值集合;
的取值集合;
(2)已知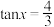 ,求
,求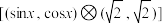 ;
;
(3)已知定义域为 的函数
的函数 满足
满足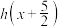 为奇函数,
为奇函数,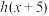 为偶函数,且
为偶函数,且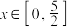 时,
时,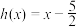 ,是否存在实数
,是否存在实数 ,使
,使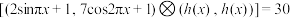 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
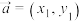 ,
,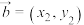 ,定义运算
,定义运算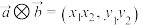 ,同时定义
,同时定义 .
.(1)若
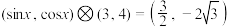 ,求实数
,求实数 的取值集合;
的取值集合;(2)已知
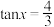 ,求
,求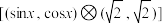 ;
;(3)已知定义域为
 的函数
的函数 满足
满足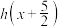 为奇函数,
为奇函数,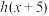 为偶函数,且
为偶函数,且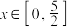 时,
时, ,是否存在实数
,是否存在实数 ,使
,使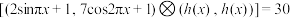 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
名校
6 . 如图,直角梯形 中,
中, ,
,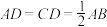 ,若
,若 为
为 三条边上的一个动点,且
三条边上的一个动点,且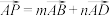 ,则下列结论中正确的是
,则下列结论中正确的是______ .(把正确结论的序号都填上)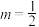 的点
的点 有且只有1个;
有且只有1个;
②满足 的点
的点 有且只有2个;
有且只有2个;
③能使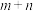 取最大值的点
取最大值的点 有且只有2个;
有且只有2个;
④能使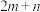 取最大值的点
取最大值的点 有无数个.
有无数个.
 中,
中, ,
,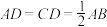 ,若
,若 为
为 三条边上的一个动点,且
三条边上的一个动点,且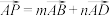 ,则下列结论中正确的是
,则下列结论中正确的是
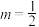 的点
的点 有且只有1个;
有且只有1个;②满足
 的点
的点 有且只有2个;
有且只有2个;③能使
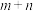 取最大值的点
取最大值的点 有且只有2个;
有且只有2个;④能使
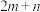 取最大值的点
取最大值的点 有无数个.
有无数个.
您最近一年使用:0次
名校
7 . 在 中,
中, ,若点
,若点 为
为 的垂心,且满足
的垂心,且满足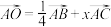 ,则
,则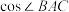 的值为( )
的值为( )
 中,
中, ,若点
,若点 为
为 的垂心,且满足
的垂心,且满足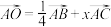 ,则
,则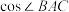 的值为( )
的值为( )A. | B. | C. | D. |
您最近一年使用:0次
2024-04-30更新
|
770次组卷
|
4卷引用:福建省福州第一中学2023-2024学年高一下学期4月第三学段模块考试数学试题
福建省福州第一中学2023-2024学年高一下学期4月第三学段模块考试数学试题(已下线)【练】专题五 平面向量的综合问题(压轴大全)山东省潍坊市部分学校2023-2024学年高一下学期第二次月考数学试题(已下线)暑假作业06 平面向量基本定理及爪子定理、等和线(系数和)的应用-【暑假分层作业】(人教A版2019必修第二册)
解题方法
8 . 如图,在 的边上作匀速运动的三个点P,S,R,当
的边上作匀速运动的三个点P,S,R,当 时,分别从A,B,C出发,当
时,分别从A,B,C出发,当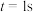 时,恰好同时到达
时,恰好同时到达 .那么这个运动过程中的定点是
.那么这个运动过程中的定点是 的( )
的( )
 的边上作匀速运动的三个点P,S,R,当
的边上作匀速运动的三个点P,S,R,当 时,分别从A,B,C出发,当
时,分别从A,B,C出发,当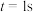 时,恰好同时到达
时,恰好同时到达 .那么这个运动过程中的定点是
.那么这个运动过程中的定点是 的( )
的( )
| A.内心 | B.外心 | C.垂心 | D.重心 |
您最近一年使用:0次
名校
解题方法
9 . 如图,在直角梯形 中,
中,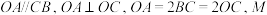 为
为 上靠近
上靠近 的三等分点,
的三等分点, 交
交 于
于 为线段
为线段 上的一个动点.
上的一个动点. 和
和 表示
表示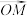 ;
;
(2)求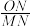 ;
;
(3)设 ,求
,求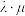 的取值范围.
的取值范围.
 中,
中,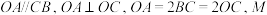 为
为 上靠近
上靠近 的三等分点,
的三等分点, 交
交 于
于 为线段
为线段 上的一个动点.
上的一个动点.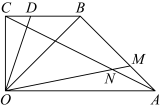
 和
和 表示
表示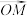 ;
;(2)求
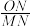 ;
;(3)设
 ,求
,求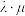 的取值范围.
的取值范围.
您最近一年使用:0次
2024-03-24更新
|
1034次组卷
|
3卷引用:云南省昆明市第一中学西山学校2023-2024学年高一下学期3月月考数学试卷
云南省昆明市第一中学西山学校2023-2024学年高一下学期3月月考数学试卷(已下线)期中考试押题卷-【帮课堂】(苏教版2019必修第二册)海南省海口市琼山华侨中学2023-2024学年高一下学期期中考试数学试卷
10 . 将所有平面向量组成的集合记作 ,f是从
,f是从 到
到 的映射,记作
的映射,记作 或
或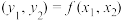 ,其中
,其中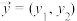 ,
,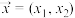 ,
, ,
, ,
, ,
, 都是实数.定义映射
都是实数.定义映射 的模为:在
的模为:在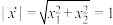 的条件下
的条件下 的最大值,记作
的最大值,记作 .若存在非零向量
.若存在非零向量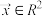 ,及实数
,及实数 使得
使得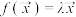 ,则称
,则称 为
为 的一个特征值.
的一个特征值.
(1)若 ,求
,求 ;
;
(2)若 ,计算
,计算 的特征值并求出相应的
的特征值并求出相应的 ;(若符合条件的向量
;(若符合条件的向量 有多个,写出其中一个即可)
有多个,写出其中一个即可)
(3)若 ,要使
,要使 有唯一的特征值,实数
有唯一的特征值,实数 ,
, ,
, ,
, 应满足什么条件?试找出一个映射
应满足什么条件?试找出一个映射 ,满足以下两个条件:①有唯一的特征值
,满足以下两个条件:①有唯一的特征值 ;②
;② ,并验证
,并验证 满足这两个条件.
满足这两个条件.
 ,f是从
,f是从 到
到 的映射,记作
的映射,记作 或
或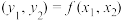 ,其中
,其中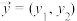 ,
,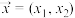 ,
, ,
, ,
, ,
, 都是实数.定义映射
都是实数.定义映射 的模为:在
的模为:在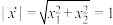 的条件下
的条件下 的最大值,记作
的最大值,记作 .若存在非零向量
.若存在非零向量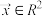 ,及实数
,及实数 使得
使得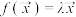 ,则称
,则称 为
为 的一个特征值.
的一个特征值.(1)若
 ,求
,求 ;
;(2)若
 ,计算
,计算 的特征值并求出相应的
的特征值并求出相应的 ;(若符合条件的向量
;(若符合条件的向量 有多个,写出其中一个即可)
有多个,写出其中一个即可)(3)若
 ,要使
,要使 有唯一的特征值,实数
有唯一的特征值,实数 ,
, ,
, ,
, 应满足什么条件?试找出一个映射
应满足什么条件?试找出一个映射 ,满足以下两个条件:①有唯一的特征值
,满足以下两个条件:①有唯一的特征值 ;②
;② ,并验证
,并验证 满足这两个条件.
满足这两个条件.
您最近一年使用:0次
2024-03-24更新
|
529次组卷
|
4卷引用:重庆市西南大学附属中学校2023-2024学年高一下学期定时检测(一)(3月月考)数学试题
重庆市西南大学附属中学校2023-2024学年高一下学期定时检测(一)(3月月考)数学试题(已下线)模块五 专题三 全真能力模拟1(高一期中模拟)(已下线)模块五 专题6 全真拔高模拟2(北师版高一期中)福建省部分学校(高中)2023-2024学年高一下学期期中联考数学试题



