11-12高二上·辽宁锦州·期末
1 . P为双曲线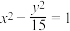 右支上一点,M,N分别是圆
右支上一点,M,N分别是圆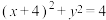 和
和 上的点,则
上的点,则 的最大值为
的最大值为__________ .
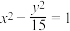 右支上一点,M,N分别是圆
右支上一点,M,N分别是圆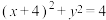 和
和 上的点,则
上的点,则 的最大值为
的最大值为
您最近一年使用:0次
2023-08-18更新
|
636次组卷
|
16卷引用:2015年全国高中数学联赛黑龙江赛区预赛试题
2015年全国高中数学联赛黑龙江赛区预赛试题黑龙江省绥化市第九中学2021-2022学年高二下学期4月月考数学试题(已下线)2010-2011年辽宁省北镇高中高二上学期期末考试数学理卷2015-2016学年江西玉山一中高二下第一次月考文科数学卷广东省佛山市2017-2018学年高二上学期期末教学质量检测数学(理)试题2(已下线)活页作业18 双曲线及其标准方程-2018年数学同步优化指导(北师大版选修2-1)2019届江苏省徐州市第一中学高三下学期开学考试数学试题北京名校2023届高三一轮总复习 第7章 解析几何 7.9 双曲线及其几何性质3.2 双曲线(已下线)人教A版2019选择性必修第一册综合测试(提升)-2023-2024学年高二数学《一隅三反》系列(人教A版2019选择性必修第一册)(已下线)3.2.1 双曲线及其标准方程(6大题型)精讲-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)(已下线)第3章 圆锥曲线与方程章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)(已下线)专题06 双曲线及其性质(4大考点11种题型)(考点清单)-2023-2024学年高二数学上学期期中考点大串讲(苏教版2019选择性必修第一册)(已下线)第02讲 3.2双曲线(1)(已下线)3.2.1 双曲线及其标准方程【第三课】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)专题11 双曲线的标准方程6种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(苏教版2019选择性必修第一册)
13-14高三上·湖北黄冈·期末
名校
2 . 若 :所有实数的平方都是正数,则
:所有实数的平方都是正数,则 为( )
为( )
 :所有实数的平方都是正数,则
:所有实数的平方都是正数,则 为( )
为( )| A.所有实数的平方都不是正数 | B.至少有一个实数的平方不是正数 |
| C.至少有一个实数的平方是正数 | D.有的实数的平方是正数 |
您最近一年使用:0次
2021-11-29更新
|
691次组卷
|
19卷引用:2013年全国高中数学联赛黑龙江赛区预赛试题
(已下线)2013年全国高中数学联赛黑龙江赛区预赛试题(已下线)2013届湖北省黄冈市高三上学期期末考试理科数学试卷(已下线)2013-2014学年河南许昌市五高二上期期末联考文科数学试卷山西省孝义市2018届高三上学期入学摸底考试数学(文)试题广东省深圳市南山区2018届高三上学期入学摸底考试(文)数学试题湖北省宜昌市葛洲坝中学2018届高三9月月考数学(文)试题(已下线)解密02 常用逻辑用语-备战2018年高考文科数学之高频考点解密(教师版)(已下线)《高频考点解密》—解密02 常用逻辑用语(已下线)第1章 3.1 全称量词与全称命题、3.2 存在量词与特称命题、3.3 全称命题与特称命题的否定(反馈达标训练)-2018年数学同步优化指导(北师大版选修2-1)(已下线)专题08集合单元复习--2020年初升高数学无忧衔接(沪教版)(已下线)考点03 全称量词与存在量词(考点专练)-备战2021年新高考数学一轮复习考点微专题(已下线)2.3全称量词与存在量词(备作业)-【上好课】2021-2022学年高一数学同步备课系列(苏教版2019必修第一册)辽宁省沈阳二中2021-2022学年高一10月份月考数学试题辽宁省沈阳市第二中学2021-2022学年高一上学期第一次月考数学试题重庆市育才中学2021-2022学年高一上学期第二次定时练习数学试题陕西省西安中学2022届高三下学期第一次仿真考试理科数学试题(已下线)2.3 全称量词命题与存在量词命题江苏省连云港市锦屏高级中学2022-2023学年高一上学期第一次月考数学试题北京名校2023届高三一轮总复习 第1章 集合与简易逻辑 1.3 常用逻辑用语
2014高三·全国·专题练习
名校
3 . 设 、
、 分别是双曲线
分别是双曲线 :
: (
( ,
, )的左、右焦点,若双曲线的右支上存在一点
)的左、右焦点,若双曲线的右支上存在一点 ,使得
,使得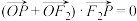 ,
, 为坐标原点,且
为坐标原点,且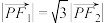 ,则双曲线
,则双曲线 的离心率为( ).
的离心率为( ).
 、
、 分别是双曲线
分别是双曲线 :
: (
( ,
, )的左、右焦点,若双曲线的右支上存在一点
)的左、右焦点,若双曲线的右支上存在一点 ,使得
,使得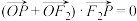 ,
, 为坐标原点,且
为坐标原点,且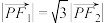 ,则双曲线
,则双曲线 的离心率为( ).
的离心率为( ).A.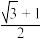 |
B.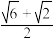 |
C.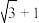 |
D.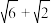 |
您最近一年使用:0次
2021-01-02更新
|
1158次组卷
|
10卷引用:2013年全国高中数学联赛黑龙江赛区预赛试题
(已下线)2013年全国高中数学联赛黑龙江赛区预赛试题黑龙江省实验中学2020-2021学年高三下学期2月月考试题(线上) 数学(理)试题(已下线)2014年高考数学(理)二轮复习体系通关训练1-9练习卷山东省寿光市第一中学2017-2018学年高二12月月考数学(文)试题江西省奉新县第一中学2017-2018学年高二上学期期末考试数学(文)试题(已下线)专题05+双曲线小题专项练习-2020-2021学年【补习教材·寒假作业】高二数学(人教A版2019)(已下线)专题13+双曲线小题专项练习-2020-2021学年【补习教材·寒假作业】高二数学(文)(人教A版)(已下线)专题13+双曲线小题专项练习-2020-2021学年【补习教材·寒假作业】高二数学(理)(人教A版)(已下线)专题13 双曲线专项练习(已下线)专题13 双曲线专项练习
名校
解题方法
4 . 已知双曲线 的左右焦点分别为
的左右焦点分别为 ,
, ,过
,过 的直线交双曲线于P,Q两点,且
的直线交双曲线于P,Q两点,且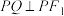 ,
, ,则双曲线的离心率为
,则双曲线的离心率为________ .
 的左右焦点分别为
的左右焦点分别为 ,
, ,过
,过 的直线交双曲线于P,Q两点,且
的直线交双曲线于P,Q两点,且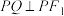 ,
, ,则双曲线的离心率为
,则双曲线的离心率为
您最近一年使用:0次
2020-08-06更新
|
3657次组卷
|
11卷引用:2018年全国高中数学联赛黑龙江省预赛
(已下线)2018年全国高中数学联赛黑龙江省预赛天津市和平区2017-2018学年高二上学期期末考试数学(文)试题天津市和平区2017-2018学年高二上学期期末考试数学(理)试题安徽省淮北市第一中学2020届高三下学期最后一卷数学(文)试题安徽省淮北市第一中学2020届高三下学期最后一卷数学(理)试题(已下线)考点43 双曲线(讲解)-2021年高考数学复习一轮复习笔记四川省绵阳市江油中学2020-2021学年高三8月第二次考试文科数学试题(已下线)第39练 双曲线-2021年高考数学(理)一轮复习小题必刷(已下线)专题3.2 双曲线-2020-2021学年高二数学同步课堂帮帮帮(人教A版2019选择性必修第一册)(已下线)考点47 双曲线-备战2021年高考数学经典小题考前必刷(新高考地区专用)(已下线)湖南省长沙市长郡中学2024届高三上学期月考(二)数学试题变式题15-18
5 . 过抛物线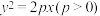 的对称轴上的定点
的对称轴上的定点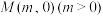 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 、
、 两点.
两点.
(1)证明: 、
、 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(2)若点 是定直线
是定直线 上的任一点,设三条直线
上的任一点,设三条直线 ,
, ,
, 的斜率分别为
的斜率分别为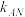 ,
,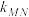 ,
,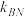 ,证明
,证明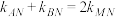
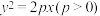 的对称轴上的定点
的对称轴上的定点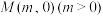 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 、
、 两点.
两点.(1)证明:
 、
、 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;(2)若点
 是定直线
是定直线 上的任一点,设三条直线
上的任一点,设三条直线 ,
, ,
, 的斜率分别为
的斜率分别为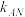 ,
,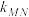 ,
,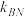 ,证明
,证明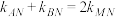
您最近一年使用:0次
2020-07-01更新
|
269次组卷
|
2卷引用:黑龙江省鸡西实验中学2020-2021学年高中教师命题大赛数学试题
11-12高二·河南安阳·阶段练习
名校
6 . 已知函数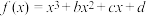 在区间
在区间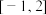 上是减函数,那么
上是减函数,那么
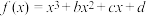 在区间
在区间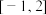 上是减函数,那么
上是减函数,那么
A.有最小值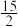 | B.有最大值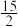 |
C.有最小值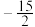 | D.有最大值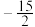 |
您最近一年使用:0次
2019-01-30更新
|
953次组卷
|
11卷引用:黑龙江省鸡西实验中学2020-2021学年高中教师命题大赛数学试题
黑龙江省鸡西实验中学2020-2021学年高中教师命题大赛数学试题(已下线)2012-2013学年河南安阳一中高二第二次阶段考试文科数学试卷2015-2016学年福建省上杭一中高二下半期理科数学试卷2016-2017学年河北省邢台市第一中学高二下学期第二次月考数学(理)试卷【校级联考】湖南省醴陵二中、醴陵四中2018-2019学年高二下学期期中联考数学(文)试题湖南省株洲市2019-2020学年高二上学期期中数学(理)试题安徽省安庆市怀宁县第二中学2019-2020学年高二下学期期中线上检测数学(理)试题安徽省安庆市怀宁县第二中学2020-2021学年高三上学期第一次月考数学试题河南新乡市省辉县市第一高级中学2020-2021学年高二下学期第一次阶段性考试数学(理)试题河南省温县第一高级中学2021-2022学年高三上学期开学考试文科数学试题广东省潮州市饶平县第二中学2020-2021学年高二下学期第一次月考数学试题
名校
7 . 已知函数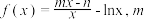 ,
,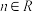 .
.
(1)若函数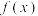 在
在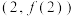 处的切线与直线
处的切线与直线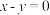 平行,求实数
平行,求实数 的值;
的值;
(2)试讨论函数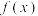 在区间
在区间 上的最大值;
上的最大值;
(3)若 时,函数
时,函数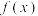 恰有两个零点
恰有两个零点 ,求证:
,求证: .
.
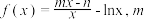 ,
,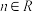 .
.(1)若函数
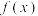 在
在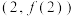 处的切线与直线
处的切线与直线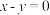 平行,求实数
平行,求实数 的值;
的值;(2)试讨论函数
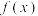 在区间
在区间 上的最大值;
上的最大值;(3)若
 时,函数
时,函数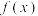 恰有两个零点
恰有两个零点 ,求证:
,求证: .
.
您最近一年使用:0次
2018-12-08更新
|
1067次组卷
|
8卷引用:2018年全国高中数学联赛黑龙江省预赛
(已下线)2018年全国高中数学联赛黑龙江省预赛2016届湖北七市教研协作体高三4月联考数学(文)试卷(已下线)《2018-2019学年同步单元双基双测AB卷》【文科数学B】第二章第二练函数图像的应用及函数与方程【校级联考】新余四中、上高二中2019届高三第一次联考数学(文)试题【市级联考】河南省洛阳市2019届高三上学期尖子生第二次联考数学文科试题辽宁省六校协作体2019-2020学年高三上学期开学考试数学(理)试题辽宁省六校协作体2019-2020学年高三上学期开学考试数学(文)试卷2019届湖南省永州市祁阳县高三下学期第二次模拟考试理科数学试题
名校
8 . 若正方形ABCD的一条边在直线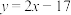 上,另外两个顶点在抛物线
上,另外两个顶点在抛物线 上.则该正方形面积的最小值为
上.则该正方形面积的最小值为________________ .
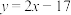 上,另外两个顶点在抛物线
上,另外两个顶点在抛物线 上.则该正方形面积的最小值为
上.则该正方形面积的最小值为
您最近一年使用:0次
2018-11-23更新
|
416次组卷
|
4卷引用:2013年全国高中数学联赛黑龙江赛区预赛试题
2013·四川成都·一模
解题方法
9 . 一个口袋中有 个白球和
个白球和 个红球(
个红球( ,且
,且 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率 ;
;
(2)若 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为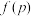 ,当
,当 为何值时,
为何值时,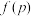 取最大值.
取最大值.
 个白球和
个白球和 个红球(
个红球( ,且
,且 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.(1)试用含
 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率 ;
;(2)若
 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;(3)记三次摸球恰有一次中奖的概率为
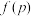 ,当
,当 为何值时,
为何值时,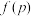 取最大值.
取最大值.
您最近一年使用:0次
2017-07-12更新
|
593次组卷
|
6卷引用:2013年全国高中数学联赛黑龙江赛区预赛试题
(已下线)2013年全国高中数学联赛黑龙江赛区预赛试题第十二届高二试题(B卷) -“枫叶新希望杯”全国数学大赛真题解析(高中版)(已下线)2013届四川省成都高新区高三4月统一检测理科数学试卷(已下线)2014届陕西省长安一中等五校高三第三次模拟理科数学试卷北京昌平临川育人学校2016-2017学年高二下学期期末考试数学(理)试题安徽省定远重点中学2017-2018学年高二下学期教学段考数学(理)试题
2014·吉林长春·一模
解题方法
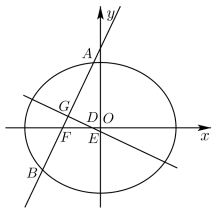
10 . 如图,椭圆
 的左焦点为
的左焦点为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点.
两点.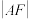 的最大值是
的最大值是 ,
,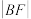 的最小值是
的最小值是 ,满足
,满足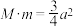 .
.
(1) 求该椭圆的离心率;
(2) 设线段 的中点为
的中点为 ,
, 的垂直平分线与
的垂直平分线与 轴和
轴和 轴分别交于
轴分别交于 两点,
两点, 是坐标原点.记
是坐标原点.记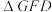 的面积为
的面积为 ,
,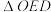 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围.

 的左焦点为
的左焦点为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点.
两点.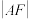 的最大值是
的最大值是 ,
,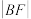 的最小值是
的最小值是 ,满足
,满足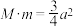 .
.(1) 求该椭圆的离心率;
(2) 设线段
 的中点为
的中点为 ,
, 的垂直平分线与
的垂直平分线与 轴和
轴和 轴分别交于
轴分别交于 两点,
两点, 是坐标原点.记
是坐标原点.记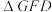 的面积为
的面积为 ,
,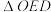 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2017-02-16更新
|
1105次组卷
|
7卷引用:2015年全国高中数学联赛黑龙江赛区预赛试题
2015年全国高中数学联赛黑龙江赛区预赛试题(已下线)2015届吉林省长春市新高三起点调研考试理科数学试卷2017届湖南长沙一中高三文月考五数学试卷(已下线)黄金30题系列 高三年级数学(文) 大题好拿分【基础版】湖南省怀化市2023届高三二模数学试题专题20平面解析几何(解答题)(已下线)专题15 圆锥曲线综合



