1 . 在平面直角坐标系 中,已知点
中,已知点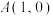 ,
,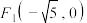 ,
,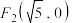 ,
, 为动点,满足
为动点,满足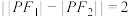 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)已知过点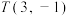 的直线
的直线 与曲线
与曲线 交于两点
交于两点 ,
, ,连接
,连接 ,
, .
.
(ⅰ)记直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,求证:
,求证: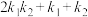 为定值;
为定值;
(ⅱ)直线 ,
, 与直线
与直线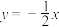 分别交于
分别交于 ,
, 两点,求
两点,求 的最小值.
的最小值.
 中,已知点
中,已知点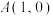 ,
,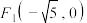 ,
,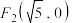 ,
, 为动点,满足
为动点,满足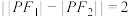 .
.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)已知过点
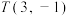 的直线
的直线 与曲线
与曲线 交于两点
交于两点 ,
, ,连接
,连接 ,
, .
.(ⅰ)记直线
 ,
, 的斜率分别为
的斜率分别为 ,
, ,求证:
,求证: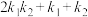 为定值;
为定值;(ⅱ)直线
 ,
, 与直线
与直线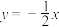 分别交于
分别交于 ,
, 两点,求
两点,求 的最小值.
的最小值.
您最近一年使用:0次
名校
2 . 已知函数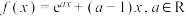 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若关于 的方程
的方程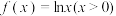 有两根
有两根 (其中
(其中 ),
),
①求 的取值范围;
的取值范围;
②当 时,求
时,求 的取值范围.
的取值范围.
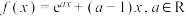 .
.(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)若关于
 的方程
的方程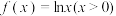 有两根
有两根 (其中
(其中 ),
),①求
 的取值范围;
的取值范围;②当
 时,求
时,求 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
3 . 已知抛物线: ,焦点为F,
,焦点为F,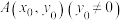 为
为 上的一个动点,
上的一个动点, 是
是 在点A处的切线,点P在
在点A处的切线,点P在 上且与点A不重合.直线PF与Γ交于B、C两点,且
上且与点A不重合.直线PF与Γ交于B、C两点,且 平分直线AB和直线AC的夹角.
平分直线AB和直线AC的夹角.
(1)求 的方程(用
的方程(用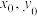 表示);
表示);
(2)若从点F发出的光线经过点A反射,证明:反射光线平行于x轴;
(3)若点A坐标为 ,求点P坐标.
,求点P坐标.
 ,焦点为F,
,焦点为F,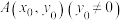 为
为 上的一个动点,
上的一个动点, 是
是 在点A处的切线,点P在
在点A处的切线,点P在 上且与点A不重合.直线PF与Γ交于B、C两点,且
上且与点A不重合.直线PF与Γ交于B、C两点,且 平分直线AB和直线AC的夹角.
平分直线AB和直线AC的夹角.(1)求
 的方程(用
的方程(用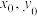 表示);
表示);(2)若从点F发出的光线经过点A反射,证明:反射光线平行于x轴;
(3)若点A坐标为
 ,求点P坐标.
,求点P坐标.
您最近一年使用:0次
名校
解题方法
4 . 已知函数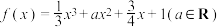 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)求 ;
;
(2)求 的极值.
的极值.
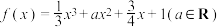 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.(1)求
 ;
;(2)求
 的极值.
的极值.
您最近一年使用:0次
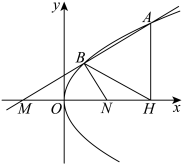
5 . 如图,在平面直角坐标系中, 和
和 是
是 轴上关于原点对称的两个点,过点
轴上关于原点对称的两个点,过点 倾斜角为
倾斜角为 的直线
的直线 与抛物线
与抛物线 交于
交于 两点,且
两点,且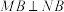 .
. 为
为 的焦点,求证:
的焦点,求证: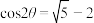 ;
;
(2)过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,若
,若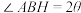 ,求直线
,求直线 的方程.
的方程.
 和
和 是
是 轴上关于原点对称的两个点,过点
轴上关于原点对称的两个点,过点 倾斜角为
倾斜角为 的直线
的直线 与抛物线
与抛物线 交于
交于 两点,且
两点,且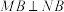 .
.
 为
为 的焦点,求证:
的焦点,求证: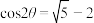 ;
;(2)过点
 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,若
,若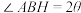 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
7日内更新
|
461次组卷
|
3卷引用:浙江省绍兴市第一中学2024届高三下学期5月模拟数学试题
名校
解题方法
6 . 帕德近似是法国数学家亨利•帕德发明的用有理多项式近似特定函数的方法.给定两个正整数 ,函数
,函数 在
在 处的
处的 阶帕德近似定义为:
阶帕德近似定义为: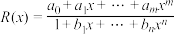 ,且满足:
,且满足: ,
,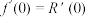 ,
, ,…,
,…,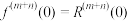 . 已知
. 已知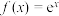 在
在 处的
处的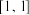 阶帕德近似为
阶帕德近似为 .注:
.注: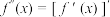 ,
,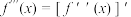 ,
,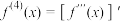 ,
,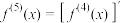 ,…
,…
(1)求实数 的值;
的值;
(2)当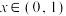 时,试比较
时,试比较 与
与 的大小,并证明;
的大小,并证明;
(3)定义数列 :
: ,
, ,求证:
,求证: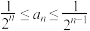 .
.
 ,函数
,函数 在
在 处的
处的 阶帕德近似定义为:
阶帕德近似定义为: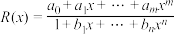 ,且满足:
,且满足: ,
,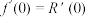 ,
, ,…,
,…,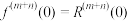 . 已知
. 已知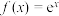 在
在 处的
处的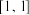 阶帕德近似为
阶帕德近似为 .注:
.注: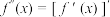 ,
,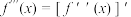 ,
,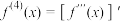 ,
,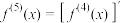 ,…
,…(1)求实数
 的值;
的值;(2)当
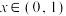 时,试比较
时,试比较 与
与 的大小,并证明;
的大小,并证明;(3)定义数列
 :
: ,
, ,求证:
,求证: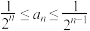 .
.
您最近一年使用:0次
2024-05-31更新
|
643次组卷
|
3卷引用:浙江省绍兴市上虞区2023-2024学年高三下学期适应性教学质量调测数学试卷
7 . 已知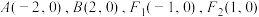 ,动点
,动点 满足
满足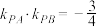 ,动点
,动点 的轨迹为曲线
的轨迹为曲线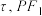 交
交 于另外一点
于另外一点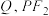 交
交 于另外一点
于另外一点 .
.
(1)求曲线 的标准方程;
的标准方程;
(2)已知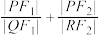 是定值,求该定值;
是定值,求该定值;
(3)求 面积的范围.
面积的范围.
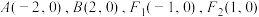 ,动点
,动点 满足
满足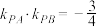 ,动点
,动点 的轨迹为曲线
的轨迹为曲线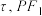 交
交 于另外一点
于另外一点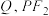 交
交 于另外一点
于另外一点 .
.(1)求曲线
 的标准方程;
的标准方程;(2)已知
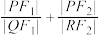 是定值,求该定值;
是定值,求该定值;(3)求
 面积的范围.
面积的范围.
您最近一年使用:0次
名校
8 . 已知函数 .
.
(1)讨论 的单调性;
的单调性;
(2)若对任意的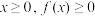 恒成立,求
恒成立,求 的范围.
的范围.
 .
.(1)讨论
 的单调性;
的单调性;(2)若对任意的
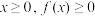 恒成立,求
恒成立,求 的范围.
的范围.
您最近一年使用:0次
名校
9 . 在平面直角坐标系中,如果将函数 的图象绕坐标原点逆时针旋转
的图象绕坐标原点逆时针旋转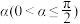 后,所得曲线仍然是某个函数的图象,则称
后,所得曲线仍然是某个函数的图象,则称 为“
为“ 旋转函数”.
旋转函数”.
(1)判断函数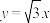 是否为“
是否为“ 旋转函数”,并说明理由;
旋转函数”,并说明理由;
(2)已知函数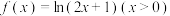 是“
是“ 旋转函数”,求
旋转函数”,求 的最大值;
的最大值;
(3)若函数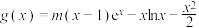 是“
是“ 旋转函数”,求
旋转函数”,求 的取值范围.
的取值范围.
 的图象绕坐标原点逆时针旋转
的图象绕坐标原点逆时针旋转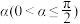 后,所得曲线仍然是某个函数的图象,则称
后,所得曲线仍然是某个函数的图象,则称 为“
为“ 旋转函数”.
旋转函数”.(1)判断函数
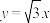 是否为“
是否为“ 旋转函数”,并说明理由;
旋转函数”,并说明理由;(2)已知函数
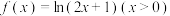 是“
是“ 旋转函数”,求
旋转函数”,求 的最大值;
的最大值;(3)若函数
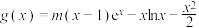 是“
是“ 旋转函数”,求
旋转函数”,求 的取值范围.
的取值范围.
您最近一年使用:0次
10 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 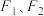 ,焦距为
,焦距为  ,离心率为
,离心率为 , 直线
, 直线 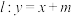 与椭圆交于
与椭圆交于  两点 (其中点
两点 (其中点  在
在  轴上方,点
轴上方,点  在
在  轴下方).
轴下方).
(1)求椭圆 的标准方程;
的标准方程;
(2)如图,将平面 沿
沿  轴折叠,使
轴折叠,使  轴正半轴和
轴正半轴和  轴所确定的半平面(平面
轴所确定的半平面(平面  )与
)与  轴 负半轴和
轴 负半轴和  轴所确定的半平面 (平面
轴所确定的半平面 (平面 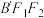 ) 垂直.
) 垂直. ,求
,求  的值;
的值;
②是否存在 ,使折叠后
,使折叠后 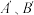 两点间的距离与折叠前
两点间的距离与折叠前  两点间的距离之比为
两点间的距离之比为 ?
?
 的左、右焦点分别为
的左、右焦点分别为 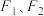 ,焦距为
,焦距为  ,离心率为
,离心率为 , 直线
, 直线 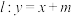 与椭圆交于
与椭圆交于  两点 (其中点
两点 (其中点  在
在  轴上方,点
轴上方,点  在
在  轴下方).
轴下方).(1)求椭圆
 的标准方程;
的标准方程;(2)如图,将平面
 沿
沿  轴折叠,使
轴折叠,使  轴正半轴和
轴正半轴和  轴所确定的半平面(平面
轴所确定的半平面(平面  )与
)与  轴 负半轴和
轴 负半轴和  轴所确定的半平面 (平面
轴所确定的半平面 (平面 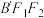 ) 垂直.
) 垂直.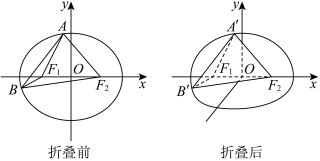
 ,求
,求  的值;
的值;②是否存在
 ,使折叠后
,使折叠后  两点间的距离与折叠前
两点间的距离与折叠前  两点间的距离之比为
两点间的距离之比为 ?
?
您最近一年使用:0次



