1 . 如图,四边形 为矩形,
为矩形,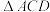 ≌
≌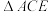 ,且二面角
,且二面角 为直二面角.
为直二面角.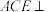 平面
平面 ;
;
(2)设 是
是 的中点,
的中点, ,二面角
,二面角 的平面角的大小为
的平面角的大小为 ,当
,当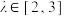 时,求
时,求 的取值范围.
的取值范围.
 为矩形,
为矩形,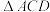 ≌
≌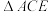 ,且二面角
,且二面角 为直二面角.
为直二面角.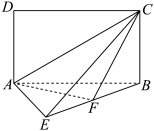
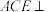 平面
平面 ;
;(2)设
 是
是 的中点,
的中点, ,二面角
,二面角 的平面角的大小为
的平面角的大小为 ,当
,当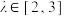 时,求
时,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-02-01更新
|
1313次组卷
|
4卷引用:湖南省株洲市第二中学2021-2022学年高二上学期第三次月考数学试卷
湖南省株洲市第二中学2021-2022学年高二上学期第三次月考数学试卷湖北省襄阳市、黄石市、宜昌市、黄冈市部分学校2023-2024学年高二上学期期末联考数学试题重庆市缙云教育联盟2024届高三下学期第二次诊断性检测数学试题(已下线)专题5 空间向量求值及范围问题【讲】(高二期中压轴专项)
名校
解题方法
2 . 已知椭圆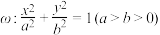 过点
过点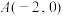 ,且
,且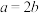 .
.
(1)求椭圆ω的方程;
(2)设O为原点,过点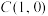 的直线l与椭圆ω交于P,Q两点,且直线l与x轴不重合,直线AP,AQ分别与y轴交于M,N两点.求证
的直线l与椭圆ω交于P,Q两点,且直线l与x轴不重合,直线AP,AQ分别与y轴交于M,N两点.求证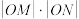 为定值.
为定值.
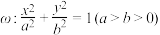 过点
过点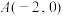 ,且
,且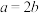 .
.(1)求椭圆ω的方程;
(2)设O为原点,过点
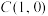 的直线l与椭圆ω交于P,Q两点,且直线l与x轴不重合,直线AP,AQ分别与y轴交于M,N两点.求证
的直线l与椭圆ω交于P,Q两点,且直线l与x轴不重合,直线AP,AQ分别与y轴交于M,N两点.求证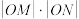 为定值.
为定值.
您最近一年使用:0次
2024-08-14更新
|
1112次组卷
|
11卷引用:北京市丰台区2020-2021学年高二上学期期末练习数学试题
北京市丰台区2020-2021学年高二上学期期末练习数学试题(已下线)专练35 综合拔高练-2021-2022学年高二数学上册同步课后专练(人版A版选择性必修第一册)江苏省连云港市2022-2023学年高三上学期期中复习数学试题新疆吐鲁番市高昌区第二中学2021-2022学年高二上学期期末考试数学(理)试题 北京市西城区北京师范大学第二附属中学2023-2024学年高二下学期期中考试数学试题北京市中央民族大学附属中学2023-2024学年高二上学期期末复习(四)数学试题广东省部分学校2025届新高三上学期开学摸底联合教学质量检测(已下线)重难点突破06 弦长问题及长度和、差、商、积问题(七大题型)(已下线)模块二 专题2 解析几何中定值、定点、定直线问题【讲】(高二期中压轴专项)(已下线)专题3 函数思想 确定定值(经典好题母题)【练】广东省揭阳市普宁市华侨中学2024-2025学年高三上学期第一次月考数学试卷
名校
解题方法
3 . 已知过点 的直线
的直线 与抛物线
与抛物线 交于
交于 两点,过线段
两点,过线段 的中点
的中点 作直线
作直线 轴,垂足为
轴,垂足为 ,且
,且 .
.
(1)求抛物线 的方程;
的方程;
(2)若 为
为 上异于点
上异于点 的任意一点,且直线
的任意一点,且直线 与直线
与直线 交于点
交于点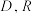 ,证明:以
,证明:以 为直径的圆过定点.
为直径的圆过定点.
 的直线
的直线 与抛物线
与抛物线 交于
交于 两点,过线段
两点,过线段 的中点
的中点 作直线
作直线 轴,垂足为
轴,垂足为 ,且
,且 .
.(1)求抛物线
 的方程;
的方程;(2)若
 为
为 上异于点
上异于点 的任意一点,且直线
的任意一点,且直线 与直线
与直线 交于点
交于点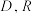 ,证明:以
,证明:以 为直径的圆过定点.
为直径的圆过定点.
您最近一年使用:0次
2023-09-28更新
|
1157次组卷
|
10卷引用:湖南省株洲市第一中学2021-2022学年高二上学期期末数学试题
湖南省株洲市第一中学2021-2022学年高二上学期期末数学试题江西省九江市2023届高三上学期第一次模拟数学(文)试题河南省三门峡市陕州中学2024届高三上学期第三次月清数学试题湖南省衡阳市衡阳县第二中学2023-2024学年高二上学期期末达标测试数学试题(B卷)(已下线)2024年全国高考名校名师联席命制型数学信息卷(四)江苏省苏州市苏州实验中学2023一2024学年高二上学期12月质量检测数学试题(已下线)专题05 抛物线8种常见考法归类(3)(已下线)专题08 抛物线的压轴题(5类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)(已下线)第08讲:圆锥曲线(大题) (必刷7大考题+7大题型)-2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019)(已下线)专题27 抛物线的简单几何性质7种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)
解题方法
4 . 在平面直角坐标系xoy中,已知椭圆C: ,F是椭圆的右焦点且椭圆C与圆M:
,F是椭圆的右焦点且椭圆C与圆M: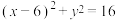 外切,又与圆N:
外切,又与圆N: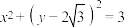 外切.
外切.
(2)已知A,B是椭圆C上关于原点对称的两点,A在x轴的上方,连接AF,BF并分别延长交椭圆C于D,E两点,证明:直线DE过定点.
 ,F是椭圆的右焦点且椭圆C与圆M:
,F是椭圆的右焦点且椭圆C与圆M: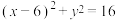 外切,又与圆N:
外切,又与圆N: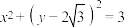 外切.
外切.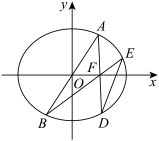
(2)已知A,B是椭圆C上关于原点对称的两点,A在x轴的上方,连接AF,BF并分别延长交椭圆C于D,E两点,证明:直线DE过定点.
您最近一年使用:0次
名校
解题方法
5 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率为
,离心率为 ,且椭圆
,且椭圆 上的点到焦点的距离的最大值为
上的点到焦点的距离的最大值为 .
.
(1)求椭圆 的方程.
的方程.
(2)设 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的不同两点,
轴对称的不同两点, 在椭圆
在椭圆 上,且点
上,且点 异于
异于 、
、 两点,
两点, 为原点,直线
为原点,直线 交
交 轴于点
轴于点 ,直线
,直线 交
交 轴于点
轴于点 ,试问
,试问 是否为定值?若为定值,求出这个定值;若不是定值,请说明理由.
是否为定值?若为定值,求出这个定值;若不是定值,请说明理由.
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率为
,离心率为 ,且椭圆
,且椭圆 上的点到焦点的距离的最大值为
上的点到焦点的距离的最大值为 .
.(1)求椭圆
 的方程.
的方程.(2)设
 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的不同两点,
轴对称的不同两点, 在椭圆
在椭圆 上,且点
上,且点 异于
异于 、
、 两点,
两点, 为原点,直线
为原点,直线 交
交 轴于点
轴于点 ,直线
,直线 交
交 轴于点
轴于点 ,试问
,试问 是否为定值?若为定值,求出这个定值;若不是定值,请说明理由.
是否为定值?若为定值,求出这个定值;若不是定值,请说明理由.
您最近一年使用:0次
2023-07-12更新
|
751次组卷
|
6卷引用:湖南省株洲市第一中学2021-2022学年高二上学期期中测试数学试卷
湖南省株洲市第一中学2021-2022学年高二上学期期中测试数学试卷河南省新乡市2022-2023学年高二下学期期末数学试题云南省曲靖市富源县2022-2023学年高二下学期期末检测数学试题内蒙古名校联盟2022-2023学年高二下学期期末考试理科数学试题内蒙古名校联盟2022-2023学年高二下学期期末考试文科数学试题(已下线)专题3.3 直线与椭圆的位置关系【八大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)
名校
6 . 如图1,已知 是直角梯形,
是直角梯形, ,
,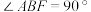 ,
,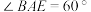 ,C、D分别为BF、AE的中点,
,C、D分别为BF、AE的中点, ,
,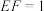 ,将直角梯形ABFE沿CD翻折,使得二面角
,将直角梯形ABFE沿CD翻折,使得二面角 的大小为60°,如图2所示,设N为BC的中点.
的大小为60°,如图2所示,设N为BC的中点. ;
;
(2)若M为AE上一点,且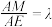 ,则当
,则当 为何值时,直线BM与平面ADE所成角的正弦值为
为何值时,直线BM与平面ADE所成角的正弦值为 .
.
 是直角梯形,
是直角梯形, ,
,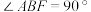 ,
,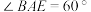 ,C、D分别为BF、AE的中点,
,C、D分别为BF、AE的中点, ,
,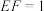 ,将直角梯形ABFE沿CD翻折,使得二面角
,将直角梯形ABFE沿CD翻折,使得二面角 的大小为60°,如图2所示,设N为BC的中点.
的大小为60°,如图2所示,设N为BC的中点.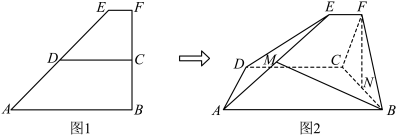
 ;
;(2)若M为AE上一点,且
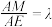 ,则当
,则当 为何值时,直线BM与平面ADE所成角的正弦值为
为何值时,直线BM与平面ADE所成角的正弦值为 .
.
您最近一年使用:0次
2023-06-20更新
|
3066次组卷
|
15卷引用:湖南省株洲市第二中学2021-2022学年高二上学期期中测试数学试卷
湖南省株洲市第二中学2021-2022学年高二上学期期中测试数学试卷贵州省卓越发展计划2022-2023学年高二下学期6月测试数学试题贵州省凯里市第一中学2022-2023学年高二下学期6月月考数学试题(已下线)第11讲 用空间向量研究距离、夹角问题11种常见考法归类-【暑假自学课】2023年新高二数学暑假精品课(人教A版2019选择性必修第一册)(已下线)第一章:空间向量与立体几何章末综合检测卷-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)(已下线)1.4.2 用空间向量研究距离、夹角问题(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)辽宁省辽东南协作体2023-2024学年高二上学期9月月考数学(B卷)试题广东省广州市真光中学2023-2024学年高二上学期9月阶段性质量检测数学试题辽宁省沈阳市第十一中学2023-2024学年高二上学期10月月考数学试题广东省广州市育才中学2023-2024学年高二上学期期中数学试题湖北省部分省级示范高中2023-2024学年高二上学期期中考试数学试题(已下线)考点15 立体几何中的折叠问题 2024届高考数学考点总动员【练】(已下线)专题03 空间向量的应用压轴题(5类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)(已下线)专题15 立体几何解答题全归类(练习)四川省高县中学校2023-2024学年高二上学期期中考试数学试卷
名校
解题方法
7 . 已知椭圆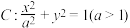 的右焦点为
的右焦点为 ,点A,B在椭圆C上,点
,点A,B在椭圆C上,点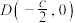 到直线
到直线 的距离为
的距离为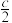 ,且
,且 的内心恰好是点D.
的内心恰好是点D.
(1)求椭圆C的标准方程;
(2)已知O为坐标原点,M,N为椭圆上不重合两点,且M,N的中点H在直线 上,求
上,求 面积的最大值.
面积的最大值.
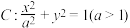 的右焦点为
的右焦点为 ,点A,B在椭圆C上,点
,点A,B在椭圆C上,点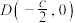 到直线
到直线 的距离为
的距离为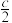 ,且
,且 的内心恰好是点D.
的内心恰好是点D.(1)求椭圆C的标准方程;
(2)已知O为坐标原点,M,N为椭圆上不重合两点,且M,N的中点H在直线
 上,求
上,求 面积的最大值.
面积的最大值.
您最近一年使用:0次
2023-05-21更新
|
650次组卷
|
3卷引用:湖南省长沙市宁乡市第一高级中学2021届高三第二次模拟考试数学试题
8 . 设椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,已知椭圆C的短轴长为
,已知椭圆C的短轴长为 ,离心率
,离心率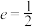 .
.
(1)求椭圆C的方程;
(2)过 的直线l交椭圆C于A、B两点,请问
的直线l交椭圆C于A、B两点,请问 的内切圆E的面积是否存在最大值?若存在,求出这个最大值及直线l的方程,若不存在,请说明理由.
的内切圆E的面积是否存在最大值?若存在,求出这个最大值及直线l的方程,若不存在,请说明理由.
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,已知椭圆C的短轴长为
,已知椭圆C的短轴长为 ,离心率
,离心率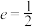 .
.(1)求椭圆C的方程;
(2)过
 的直线l交椭圆C于A、B两点,请问
的直线l交椭圆C于A、B两点,请问 的内切圆E的面积是否存在最大值?若存在,求出这个最大值及直线l的方程,若不存在,请说明理由.
的内切圆E的面积是否存在最大值?若存在,求出这个最大值及直线l的方程,若不存在,请说明理由.
您最近一年使用:0次
9 . 已知椭圆 ,左、右顶点分别为P,Q,上顶点为K,原点为O,
,左、右顶点分别为P,Q,上顶点为K,原点为O, 的面积为
的面积为 ,两焦点与短轴的一个顶点构成等边三角形,过点
,两焦点与短轴的一个顶点构成等边三角形,过点 且斜率不为
且斜率不为 的直线
的直线 与椭圆
与椭圆 交于不同的两点A,B.
交于不同的两点A,B.
(1)求椭圆 的标准方程;
的标准方程;
(2)求 面积的最大值;
面积的最大值;
(3)直线PA与直线 交于点
交于点 ,试问B,Q,
,试问B,Q, 三点是否共线?若共线,请证明;若不共线,请说明理由.
三点是否共线?若共线,请证明;若不共线,请说明理由.
 ,左、右顶点分别为P,Q,上顶点为K,原点为O,
,左、右顶点分别为P,Q,上顶点为K,原点为O, 的面积为
的面积为 ,两焦点与短轴的一个顶点构成等边三角形,过点
,两焦点与短轴的一个顶点构成等边三角形,过点 且斜率不为
且斜率不为 的直线
的直线 与椭圆
与椭圆 交于不同的两点A,B.
交于不同的两点A,B.(1)求椭圆
 的标准方程;
的标准方程;(2)求
 面积的最大值;
面积的最大值;(3)直线PA与直线
 交于点
交于点 ,试问B,Q,
,试问B,Q, 三点是否共线?若共线,请证明;若不共线,请说明理由.
三点是否共线?若共线,请证明;若不共线,请说明理由.
您最近一年使用:0次
名校
解题方法
10 . 已知椭圆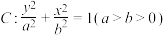 的上、下焦点分别为
的上、下焦点分别为 ,
, ,离心率为
,离心率为 ,过点
,过点 作直线
作直线 (与
(与 轴不重合)交椭圆
轴不重合)交椭圆 于
于 ,
, 两点,
两点, 的周长为
的周长为 .
.
(1)求椭圆C的标准方程;
(2)若点A是椭圆 的上顶点,设直线
的上顶点,设直线 ,
, ,
, 的斜率分别为
的斜率分别为 ,
, ,
, ,当
,当 时,求证:
时,求证: 为定值.
为定值.
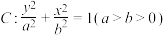 的上、下焦点分别为
的上、下焦点分别为 ,
, ,离心率为
,离心率为 ,过点
,过点 作直线
作直线 (与
(与 轴不重合)交椭圆
轴不重合)交椭圆 于
于 ,
, 两点,
两点, 的周长为
的周长为 .
.(1)求椭圆C的标准方程;
(2)若点A是椭圆
 的上顶点,设直线
的上顶点,设直线 ,
, ,
, 的斜率分别为
的斜率分别为 ,
, ,
, ,当
,当 时,求证:
时,求证: 为定值.
为定值.
您最近一年使用:0次
2023-05-06更新
|
913次组卷
|
5卷引用:湖南省株洲市第一中学2021届高三第一次模拟检测数学试题



