名校
解题方法
1 . 一个质点在随机外力的作用下,从平面直角坐标系的原点 出发,每隔1秒等可能地向上、向下、向左或向右移动一个单位.
出发,每隔1秒等可能地向上、向下、向左或向右移动一个单位.
(1)共移动两次,求质点与原点距离的分布列和数学期望;
(2)分别求移动4次和移动6次质点回到原点的概率;
(3)若共移动 次(
次( 大于0,且
大于0,且 为偶数),求证:质点回到原点的概率为
为偶数),求证:质点回到原点的概率为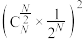 .
.
 出发,每隔1秒等可能地向上、向下、向左或向右移动一个单位.
出发,每隔1秒等可能地向上、向下、向左或向右移动一个单位.(1)共移动两次,求质点与原点距离的分布列和数学期望;
(2)分别求移动4次和移动6次质点回到原点的概率;
(3)若共移动
 次(
次( 大于0,且
大于0,且 为偶数),求证:质点回到原点的概率为
为偶数),求证:质点回到原点的概率为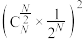 .
.
您最近一年使用:0次
名校
解题方法
2 . 手机完全充满电量,在开机不使用的状态下,电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间.为
了解A,B两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取A,B两个型号的手机各7台,在相同条件下进行测试,统计结果如下:
其中, ,
, 是正整数,且
是正整数,且 .
.
(1)该卖场有56台A型手机,试估计其中待机时间不少于123小时的台数;
(2)从A型号被测试的7台手机中随机抽取4台,记待机时间大于123小时的台数为 ,求
,求 的分布列;
的分布列;
(3)设A,B两个型号被测试手机待机时间的平均值相等,当B型号被测试手机待机时间的方差最小时,写出 ,
, 的值(结论不要求证明).
的值(结论不要求证明).
了解A,B两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取A,B两个型号的手机各7台,在相同条件下进行测试,统计结果如下:
手机编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
A型待机时间 | 120 | 125 | 122 | 124 | 124 | 123 | 123 |
B型待机时间 | 118 | 123 | 127 | 120 | 124 |
|
|
 ,
, 是正整数,且
是正整数,且 .
.(1)该卖场有56台A型手机,试估计其中待机时间不少于123小时的台数;
(2)从A型号被测试的7台手机中随机抽取4台,记待机时间大于123小时的台数为
 ,求
,求 的分布列;
的分布列;(3)设A,B两个型号被测试手机待机时间的平均值相等,当B型号被测试手机待机时间的方差最小时,写出
 ,
, 的值(结论不要求证明).
的值(结论不要求证明).
您最近一年使用:0次
2024-05-22更新
|
240次组卷
|
2卷引用:河北省邢台市南宫中学2024届高三下学期高考模拟数学试题
名校
3 . 甲、乙、丙三人进行传球游戏,每次投掷一枚质地均匀的正方体骰子决定传球的方式:当球在甲手中时,若骰子点数大于3,则甲将球传给乙,若点数不大于3,则甲将球保留;当球在乙手中时,若骰子点数大于4,则乙将球传给甲,若点数不大于4,则乙将球传给丙;当球在丙手中时,若骰子点数大于3,则丙将球传给甲,若骰子点数不大于3,则丙将球传给乙.初始时,球在甲手中.
(1)设前三次投掷骰子后,球在甲手中的次数为 ,求随机变量
,求随机变量 的分布列和数学期望;
的分布列和数学期望;
(2)投掷 次骰子后
次骰子后 ,记球在乙手中的概率为
,记球在乙手中的概率为 ,求数列
,求数列 的通项公式;
的通项公式;
(3)设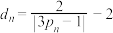 ,求证:
,求证: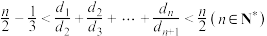 .
.
(1)设前三次投掷骰子后,球在甲手中的次数为
 ,求随机变量
,求随机变量 的分布列和数学期望;
的分布列和数学期望;(2)投掷
 次骰子后
次骰子后 ,记球在乙手中的概率为
,记球在乙手中的概率为 ,求数列
,求数列 的通项公式;
的通项公式;(3)设
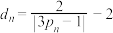 ,求证:
,求证: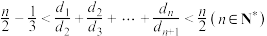 .
.
您最近一年使用:0次
2024-03-13更新
|
1657次组卷
|
3卷引用:湖北省武汉市(武汉六中)部分重点中学2024届高三第二次联考数学试题变式题17-22
(已下线)湖北省武汉市(武汉六中)部分重点中学2024届高三第二次联考数学试题变式题17-22河北省正定中学2024届高三三轮复习模拟试题数学(二)2024年河南省普通高中毕业班高考适应性测试数学试题
4 . 某人投掷两枚骰子,取其中一枚的点数记为点 的横坐标
的横坐标 ,另一枚的点数记为点
,另一枚的点数记为点 的纵坐标
的纵坐标 ,令事件
,令事件 “
“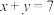 ”,事件
”,事件 “
“ 为奇数”.
为奇数”.
(1)证明:事件 相互独立;
相互独立;
(2)若连续抛掷这两枚骰子三次,求点 在圆
在圆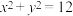 内的次数
内的次数 的分布列与期望.
的分布列与期望.
 的横坐标
的横坐标 ,另一枚的点数记为点
,另一枚的点数记为点 的纵坐标
的纵坐标 ,令事件
,令事件 “
“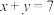 ”,事件
”,事件 “
“ 为奇数”.
为奇数”.(1)证明:事件
 相互独立;
相互独立;(2)若连续抛掷这两枚骰子三次,求点
 在圆
在圆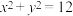 内的次数
内的次数 的分布列与期望.
的分布列与期望.
您最近一年使用:0次
解题方法
5 . 某箱中有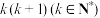 个除颜色之外均相同的球,
个除颜色之外均相同的球, 已知.箱中1个球为白球,其余为黑球.现在该箱中进行一取球实验:每次从箱中等可能地取出一个球,若取出白球或取球
已知.箱中1个球为白球,其余为黑球.现在该箱中进行一取球实验:每次从箱中等可能地取出一个球,若取出白球或取球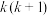 次后结束实验,否则进行相应操作进行下一次取球.设实验结束时的取球次数为
次后结束实验,否则进行相应操作进行下一次取球.设实验结束时的取球次数为 .
.
(1)若取出黑球后放回箱中,求 的数学期望
的数学期望 ;
;
(2)若取出黑球后替换为白球放回箱中,求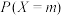 的最大值
的最大值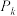 ,并证明:
,并证明: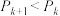 .
.
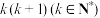 个除颜色之外均相同的球,
个除颜色之外均相同的球, 已知.箱中1个球为白球,其余为黑球.现在该箱中进行一取球实验:每次从箱中等可能地取出一个球,若取出白球或取球
已知.箱中1个球为白球,其余为黑球.现在该箱中进行一取球实验:每次从箱中等可能地取出一个球,若取出白球或取球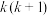 次后结束实验,否则进行相应操作进行下一次取球.设实验结束时的取球次数为
次后结束实验,否则进行相应操作进行下一次取球.设实验结束时的取球次数为 .
.(1)若取出黑球后放回箱中,求
 的数学期望
的数学期望 ;
;(2)若取出黑球后替换为白球放回箱中,求
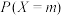 的最大值
的最大值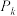 ,并证明:
,并证明: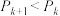 .
.
您最近一年使用:0次
解题方法
6 . 某民营学校为增强实力与影响力,大力招揽名师、建设校园硬件设施,近5年该校招生人数的数据如下表:
(1)由表中数据可看出,可用线性回归模型拟合 与
与 的关系,请用相关系数加以证明;
的关系,请用相关系数加以证明;
(2)求 关于
关于 的回归直线方程,并预测当年份序号为7时该校的招生人数.
的回归直线方程,并预测当年份序号为7时该校的招生人数.
参考数据: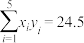 ,
, ,
, .
.
参考公式:相关系数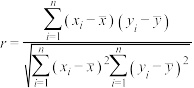 ,回归方程
,回归方程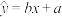 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为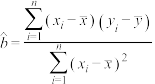 ,
, .
.
年份序号x | 1 | 2 | 3 | 4 | 5 |
招生人数y/千人 | 0.8 | 1 | 1.3 | 1.7 | 2.2 |
 与
与 的关系,请用相关系数加以证明;
的关系,请用相关系数加以证明;(2)求
 关于
关于 的回归直线方程,并预测当年份序号为7时该校的招生人数.
的回归直线方程,并预测当年份序号为7时该校的招生人数.参考数据:
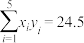 ,
, ,
, .
.参考公式:相关系数
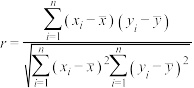 ,回归方程
,回归方程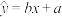 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为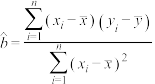 ,
, .
.
您最近一年使用:0次
2024-03-21更新
|
1040次组卷
|
6卷引用:河北省邯郸市2024届高三第三次调研考试考试数学试题
河北省邯郸市2024届高三第三次调研考试考试数学试题(已下线)专题8.5 成对数据的统计分析全章十一大基础题型归纳(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)河南省南阳市华龙高级中学2023-2024学年高二下学期3月月考数学试题陕西省宝鸡市2024届高三下学期高考模拟检测(三)理科数学试题陕西省宝鸡市2024届高三下学期高考模拟检测(三)文科数学试题
名校
7 . 已知在一个不透明的盒中装有一个白球和两个红球(小球除颜色不同,其余完全相同),某抽球试验的规则如下:试验者在每一轮需有放回地抽取两次,每次抽取一个小球,从第一轮开始,若试验者在某轮中的两次均抽到白球,则该试验成功,并停止试验.否则再将一个黄球(与盒中小球除颜色不同,其余完全相同)放入盒中,然后继续进行下一轮试验.
(1)若规定试验者甲至多可进行三轮试验(若第三轮不成功,也停止试验),记甲进行的试验轮数为随机变量 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)若规定试验者乙至多可进行 轮试验(若第
轮试验(若第 轮不成功,也停止试验),记乙在第
轮不成功,也停止试验),记乙在第 轮使得试验成功的概率为
轮使得试验成功的概率为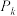 ,则乙能试验成功的概率为
,则乙能试验成功的概率为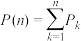 ,证明:
,证明: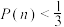 .
.
(1)若规定试验者甲至多可进行三轮试验(若第三轮不成功,也停止试验),记甲进行的试验轮数为随机变量
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)若规定试验者乙至多可进行
 轮试验(若第
轮试验(若第 轮不成功,也停止试验),记乙在第
轮不成功,也停止试验),记乙在第 轮使得试验成功的概率为
轮使得试验成功的概率为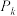 ,则乙能试验成功的概率为
,则乙能试验成功的概率为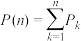 ,证明:
,证明: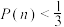 .
.
您最近一年使用:0次
名校
解题方法
8 . 某排球教练带领甲、乙两名排球主力运动员训练排球的接球与传球,首先由教练第一次传球给甲、乙中的某位运动员,然后该运动员再传回教练.每次教练接球后按下列规律传球:若教练上一次是传给某运动员,则这次有 的概率再传给该运动员,有
的概率再传给该运动员,有 的概率传给另一位运动员.已知教练第一次传给了甲运动员,且教练第
的概率传给另一位运动员.已知教练第一次传给了甲运动员,且教练第 次传球传给甲运动员的概率为
次传球传给甲运动员的概率为 .
.
(1)求 ,
, ;
;
(2)求 的表达式;
的表达式;
(3)设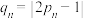 ,证明:
,证明: .
.
 的概率再传给该运动员,有
的概率再传给该运动员,有 的概率传给另一位运动员.已知教练第一次传给了甲运动员,且教练第
的概率传给另一位运动员.已知教练第一次传给了甲运动员,且教练第 次传球传给甲运动员的概率为
次传球传给甲运动员的概率为 .
.(1)求
 ,
, ;
;(2)求
 的表达式;
的表达式;(3)设
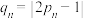 ,证明:
,证明: .
.
您最近一年使用:0次
2023-12-05更新
|
2193次组卷
|
11卷引用:河北省部分重点高中2024届高三高考模拟数学试题
河北省部分重点高中2024届高三高考模拟数学试题(已下线)黄金卷04(已下线)专题8-2分布列综合归类-2(已下线)【一题多变】传球问题 构造数列(已下线)第二章 概率 专题三 独立事件 微点3 独立事件综合训练【培优版】(已下线)第五章 概率统计创新问题 专题二 概率统计与数列交汇 微点3 概率统计与数列交汇综合训练【基础版】(已下线)第五章 概率统计创新问题 专题二 概率统计与数列交汇 微点1 概率统计与数列交汇(一)【培优版】江西省上饶市广丰中学2023-2024学年高一上学期12月月考数学试题(已下线)模块二 专题5 概率中的创新问题辽宁省锦州市2023-2024学年高二下学期期末考试数学试卷安徽省合肥市第四中学2025届高三上学期教学诊断检测(二)数学试题
名校
9 . 甲、乙两人进行象棋比赛,赛前每人发3枚筹码.一局后负的一方,需将自己的一枚筹码给对方;若平局,双方的筹码不动,当一方无筹码时,比赛结束,另一方最终获胜.由以往两人的比赛结果可知,在一局中甲胜的概率为0.3、乙胜的概率为0.2.
(1)第一局比赛后,甲的筹码个数记为 ,求
,求 的分布列和期望;
的分布列和期望;
(2)求四局比赛后,比赛结束的概率;
(3)若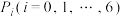 表示“在甲所得筹码为
表示“在甲所得筹码为 枚时,最终甲获胜的概率”,则
枚时,最终甲获胜的概率”,则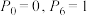 .证明:
.证明: 为等比数列.
为等比数列.
(1)第一局比赛后,甲的筹码个数记为
 ,求
,求 的分布列和期望;
的分布列和期望;(2)求四局比赛后,比赛结束的概率;
(3)若
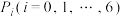 表示“在甲所得筹码为
表示“在甲所得筹码为 枚时,最终甲获胜的概率”,则
枚时,最终甲获胜的概率”,则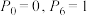 .证明:
.证明: 为等比数列.
为等比数列.
您最近一年使用:0次
2023-07-20更新
|
1995次组卷
|
7卷引用:河北省张家口市2023届高三三模数学试题
河北省张家口市2023届高三三模数学试题(已下线)微考点7-2 递推方法计算概率与一维马尔科夫过程(数列与概率结合)(已下线)第五章 概率统计创新问题 专题二 概率统计与数列交汇 微点2 概率统计与数列交汇(二)【培优版】山西省运城市运城中学2023届高三第二次模拟数学试题福建省福州市四校2022-2023学年高二下学期期末联考数学试题湖北省武汉市第四十九中学2024届高三上学期九月调考模拟数学试题(二)(已下线)2024届高三开学摸底考试
解题方法
10 . 第31届世界大学生夏季运动会将于今年在我国成都举行.某体校田径队正在积极备战,考核设有100米、400米和1500米三个项目,需要选手依次完成考核,成绩合格后的积分分别记为 ,
, 和
和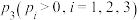 ,总成绩为累计积分和.考核规定:项目考核逐级进阶,即选手只有在低一级里程项目考核合格后,才能进行下一级较高里程项目的考核,否则考核终止.对于100米和400米项目,每个项目选手必须考核2次,且全部达标才算合格;对于1500米项目,选手必须考核3次,但只要达标2次及以上就算合格.已知选手甲三个项目的达标率依次为
,总成绩为累计积分和.考核规定:项目考核逐级进阶,即选手只有在低一级里程项目考核合格后,才能进行下一级较高里程项目的考核,否则考核终止.对于100米和400米项目,每个项目选手必须考核2次,且全部达标才算合格;对于1500米项目,选手必须考核3次,但只要达标2次及以上就算合格.已知选手甲三个项目的达标率依次为 ,
, ,
, ,选手乙三个项目的达标率依次为
,选手乙三个项目的达标率依次为 ,
,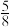 ,
, ,每次考核是否达标相互独立.
,每次考核是否达标相互独立.
(1)用 表示选手甲考核积分的总成绩,求
表示选手甲考核积分的总成绩,求 的分布列和数学期望;
的分布列和数学期望;
(2)证明:无论 ,
, 和
和 取何值,选手甲考核积分总成绩的数学期望值都大于选手乙考核积分总成绩的数学期望值.
取何值,选手甲考核积分总成绩的数学期望值都大于选手乙考核积分总成绩的数学期望值.
 ,
, 和
和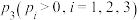 ,总成绩为累计积分和.考核规定:项目考核逐级进阶,即选手只有在低一级里程项目考核合格后,才能进行下一级较高里程项目的考核,否则考核终止.对于100米和400米项目,每个项目选手必须考核2次,且全部达标才算合格;对于1500米项目,选手必须考核3次,但只要达标2次及以上就算合格.已知选手甲三个项目的达标率依次为
,总成绩为累计积分和.考核规定:项目考核逐级进阶,即选手只有在低一级里程项目考核合格后,才能进行下一级较高里程项目的考核,否则考核终止.对于100米和400米项目,每个项目选手必须考核2次,且全部达标才算合格;对于1500米项目,选手必须考核3次,但只要达标2次及以上就算合格.已知选手甲三个项目的达标率依次为 ,
, ,
, ,选手乙三个项目的达标率依次为
,选手乙三个项目的达标率依次为 ,
,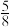 ,
, ,每次考核是否达标相互独立.
,每次考核是否达标相互独立.(1)用
 表示选手甲考核积分的总成绩,求
表示选手甲考核积分的总成绩,求 的分布列和数学期望;
的分布列和数学期望;(2)证明:无论
 ,
, 和
和 取何值,选手甲考核积分总成绩的数学期望值都大于选手乙考核积分总成绩的数学期望值.
取何值,选手甲考核积分总成绩的数学期望值都大于选手乙考核积分总成绩的数学期望值.
您最近一年使用:0次
2023-05-05更新
|
1529次组卷
|
5卷引用:河北省名校2023届高三5月模拟数学试题
河北省名校2023届高三5月模拟数学试题2023 年河北省普通高中预测卷数学试题(已下线)专题11 统计与概率(解密讲义)(已下线)第三章 随机变量及其分布列 专题四 随机变量分布列、期望、方差的应用 微点1 概率分布在生活、生产实践中的应用(一)【培优版】(已下线)2023年全国卷(老教材)理科数学预测卷