21-22高二·全国·课后作业
解题方法
1 . 已知随机变量X的分布列如下表:
求D(X)和 .
.
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 |
 .
.
您最近一年使用:0次
2022-03-08更新
|
284次组卷
|
4卷引用:3.2 离散型随机变量的方差
20-21高二·江苏·课后作业
解题方法
2 . 如果随机变量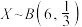 ,那么
,那么 等于( ).
等于( ).
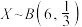 ,那么
,那么 等于( ).
等于( ).| A.1 | B.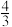 | C.2 | D.6 |
您最近一年使用:0次
2021-12-10更新
|
195次组卷
|
6卷引用:8.3正态分布
20-21高二·江苏·课后作业
解题方法
3 . 甲、乙、丙3人独立地破译某个密码,每人译出此密码的概率均为0.25.设随机变量X表示译出密码的人数,求 ,
,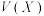 和
和 .
.
 ,
,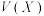 和
和 .
.
您最近一年使用:0次
2021-12-10更新
|
131次组卷
|
4卷引用:8.2离散型随机变量及其分布列
20-21高二·江苏·课后作业
解题方法
4 . 投资A,B两种股票,每股收益的分布列分别如表所示.
股票A收益的分布列
股票B收益的分布列
(1)投资哪种股票的期望收益大?
(2)投资哪种股票的风险较高?
股票A收益的分布列
收益X/元 |
| 0 | 2 |
概率 | 0.1 | 0.3 | 0.6 |
收益Y/元 | 0 | 1 | 2 |
概率 | 0.3 | 0.4 | 0.3 |
(2)投资哪种股票的风险较高?
您最近一年使用:0次
2021-12-06更新
|
445次组卷
|
6卷引用:8.2离散型随机变量及其分布列
(已下线)8.2离散型随机变量及其分布列8.2.2离散型随机变量的数字特征(备作业)-【上好课】2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第二册)新疆博湖县奇石中学2022-2023学年高二下学期期末考试数学试题人教A版(2019)选择性必修第三册课本例题7.3 离散型随机变量的数字特征(已下线)【一题多变】决策问题 期望方差(已下线)7.3离散型随机变量的数字特征 第一练 练好课本试题
20-21高二·江苏·课后作业
解题方法
5 . 某人每次射击命中目标的概率为0.8,现连续射击3次,求击中目标的次数X的均值和方差.
您最近一年使用:0次
2021-12-06更新
|
571次组卷
|
3卷引用:8.2离散型随机变量及其分布列
20-21高二·江苏·课后作业
名校
解题方法
6 . 假定某射手每次射击命中目标的概率为 .现有3发子弹,该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,求:
.现有3发子弹,该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,求:
(1)X的概率分布;
(2)均值 ;
;
(3)标准差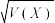 .
.
 .现有3发子弹,该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,求:
.现有3发子弹,该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,求:(1)X的概率分布;
(2)均值
 ;
;(3)标准差
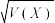 .
.
您最近一年使用:0次
2021-12-06更新
|
478次组卷
|
6卷引用:8.2离散型随机变量及其分布列
(已下线)8.2离散型随机变量及其分布列苏教版(2019) 选修第二册 名师导学 第八章 习题 8.2吉林省长春市第六中学2021-2022学年高二下学期线上教学反馈测试(第一学程考试)数学试题苏教版(2019)选择性必修第二册课本习题 习题8.2(3)(已下线)专题7.3 离散型随机变量的数字特征【七大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第三章 随机变量及其分布列 专题二 随机变量的方差 微点1 随机变量的方差【基础版】
20-21高二·江苏·课后作业
7 . 1.设随机变量X的概率分布如下表所示,试求X的均值和标准差.
X | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
您最近一年使用:0次
2021-12-06更新
|
160次组卷
|
4卷引用:8.2离散型随机变量及其分布列
(已下线)8.2离散型随机变量及其分布列苏教版(2019) 选修第二册 名师导学 第八章 8.2.3 二项分布(已下线)7.3.2 离散型随机变量的方差(1)苏教版(2019)选择性必修第二册课本习题8.2.3 二项分布
20-21高二·江苏·课后作业
解题方法
8 . 某商家有一台电话交换机,其中5个分机专供与顾客通话.设每个分机在 内平均占线
内平均占线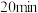 ,并且各个分机是否占线是相互独立的,求任一时刻占线的分机数目X的均值与方差.
,并且各个分机是否占线是相互独立的,求任一时刻占线的分机数目X的均值与方差.
 内平均占线
内平均占线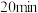 ,并且各个分机是否占线是相互独立的,求任一时刻占线的分机数目X的均值与方差.
,并且各个分机是否占线是相互独立的,求任一时刻占线的分机数目X的均值与方差.
您最近一年使用:0次
2021-12-06更新
|
161次组卷
|
3卷引用:8.2离散型随机变量及其分布列
20-21高二·江苏·课后作业
解题方法
9 . 设随机变量X的概率分布如下表.
对题中的随机变量X,分别求:
(1)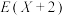 ,
, ,
, ;
;
(2) ,
,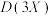 ,
,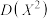 ;
;
(3)分别考察它们与 ,
, 之间的关系,你能得到随机变量的均值和方差的哪些性质?
之间的关系,你能得到随机变量的均值和方差的哪些性质?
X | 1 | 2 | 3 | 4 | 5 |
P | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
(1)
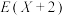 ,
, ,
, ;
;(2)
 ,
,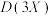 ,
,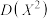 ;
;(3)分别考察它们与
 ,
, 之间的关系,你能得到随机变量的均值和方差的哪些性质?
之间的关系,你能得到随机变量的均值和方差的哪些性质?
您最近一年使用:0次
2021-12-06更新
|
449次组卷
|
6卷引用:8.2离散型随机变量及其分布列
(已下线)8.2离散型随机变量及其分布列苏教版(2019) 选修第二册 名师导学 第八章 习题 8.28.2.2离散型随机变量的数字特征(备作业)-【上好课】2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第二册)(已下线)离散型随机变量的数字特征(已下线)7.3.2 离散型随机变量的方差(2)苏教版(2019)选择性必修第二册课本习题 习题8.2(2)
20-21高二·江苏·课后作业
10 . 袋中有形状、大小完全相同的3个球,编号分别为1,2,3,在其中取出2个球,以X表示取出的2个球中的最大号码.
(1)写出X的分布列;
(2)求X的均值与方差.
(1)写出X的分布列;
(2)求X的均值与方差.
您最近一年使用:0次
2021-12-06更新
|
166次组卷
|
3卷引用:8.2离散型随机变量及其分布列





