名校
1 . 已知函数 ,则下列结论正确的是( )
,则下列结论正确的是( )
 ,则下列结论正确的是( )
,则下列结论正确的是( )A.函数 有且只有一个零点 有且只有一个零点 |
B.若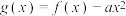 有且只有一个零点,则 有且只有一个零点,则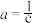 |
C.若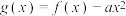 有两个极值点,则 有两个极值点,则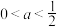 |
D.当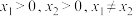 时,总有 时,总有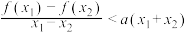 ,则 ,则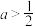 |
您最近一年使用:0次
名校
解题方法
2 . 已知正实数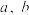 满足
满足 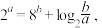 则( )
则( )
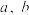 满足
满足 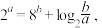 则( )
则( )A. | B. | C.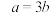 | D. |
您最近一年使用:0次
2024-05-09更新
|
652次组卷
|
2卷引用:重庆市2024年普通高等学校招生全国统一考试高考模拟调研卷(五)数学试题
3 . 已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, ,左、右顶点分别为
,左、右顶点分别为 ,
, ,
, 为坐标原点,直线
为坐标原点,直线 交双曲线
交双曲线 的右支于
的右支于 ,
, 两点(不同于右顶点),且与双曲线
两点(不同于右顶点),且与双曲线 的两条渐近线分别交于
的两条渐近线分别交于 ,
, 两点,则( )
两点,则( )
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,左、右顶点分别为
,左、右顶点分别为 ,
, ,
, 为坐标原点,直线
为坐标原点,直线 交双曲线
交双曲线 的右支于
的右支于 ,
, 两点(不同于右顶点),且与双曲线
两点(不同于右顶点),且与双曲线 的两条渐近线分别交于
的两条渐近线分别交于 ,
, 两点,则( )
两点,则( )A. 为定值 为定值 |
B. |
C.点 到两条渐近线的距离之和的最小值为 到两条渐近线的距离之和的最小值为 |
D.不存在直线 使 使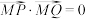 |
您最近一年使用:0次
2024-05-08更新
|
798次组卷
|
3卷引用:重庆市乌江新高考协作体2024届高考模拟监测(一)数学试题
名校
解题方法
4 . 已知向量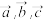 满足:
满足: 为单位向量,且
为单位向量,且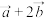 与
与 相互垂直,又对任意
相互垂直,又对任意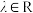 不等式
不等式 恒成立,若
恒成立,若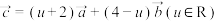 ,则
,则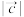 的最小值为( )
的最小值为( )
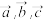 满足:
满足: 为单位向量,且
为单位向量,且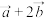 与
与 相互垂直,又对任意
相互垂直,又对任意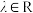 不等式
不等式 恒成立,若
恒成立,若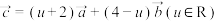 ,则
,则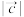 的最小值为( )
的最小值为( )| A.4 | B.5 | C.6 | D.7 |
您最近一年使用:0次
5 . 1712年英国数学家布鲁克·泰勒提出了著名的泰勒公式,该公式利用了多项式函数曲线来逼近任意一个原函数曲线,该公式在近似计算,函数拟合,计算机科学上有着举足轻重的作用.如下列常见函数的 阶泰勒展开式为:
阶泰勒展开式为:

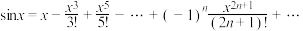
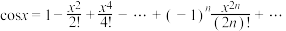
其中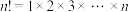 ,读作
,读作 的阶乘.
的阶乘.
1748年瑞士数学家莱昂哈德·欧拉在泰勒公式的灵感下创造了人类数学最美妙的公式,即欧拉公式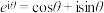 ,特别的欧拉恒等式
,特别的欧拉恒等式 被后世称为“上帝公式”.欧拉公式建立了复数域中指数函数与圆函数(正余弦函数)的关系,利用欧拉公式还可以完成圆的
被后世称为“上帝公式”.欧拉公式建立了复数域中指数函数与圆函数(正余弦函数)的关系,利用欧拉公式还可以完成圆的 等分,即棣莫弗定理
等分,即棣莫弗定理 的应用.
的应用.
(1)请写出复数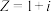 的三角形式,并利用泰勒展开式估算出
的三角形式,并利用泰勒展开式估算出 的3阶近似值(精确到0.001);
的3阶近似值(精确到0.001);
(2)请根据上述材料证明欧拉公式,并计算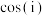 与
与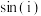 ;
;
(3)记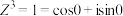 ,由棣莫弗定理得
,由棣莫弗定理得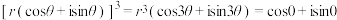 ,从而得
,从而得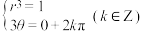 ,复数
,复数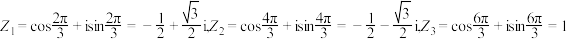 ,我们称其为1在复数域内的三次方根. 若
,我们称其为1在复数域内的三次方根. 若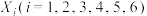 为64在复数域内的6次方根.求
为64在复数域内的6次方根.求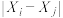 取值构成的集合,其中
取值构成的集合,其中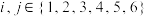 .
.
 阶泰勒展开式为:
阶泰勒展开式为:
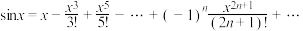
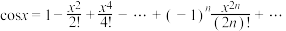
其中
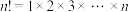 ,读作
,读作 的阶乘.
的阶乘.1748年瑞士数学家莱昂哈德·欧拉在泰勒公式的灵感下创造了人类数学最美妙的公式,即欧拉公式
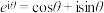 ,特别的欧拉恒等式
,特别的欧拉恒等式 被后世称为“上帝公式”.欧拉公式建立了复数域中指数函数与圆函数(正余弦函数)的关系,利用欧拉公式还可以完成圆的
被后世称为“上帝公式”.欧拉公式建立了复数域中指数函数与圆函数(正余弦函数)的关系,利用欧拉公式还可以完成圆的 等分,即棣莫弗定理
等分,即棣莫弗定理 的应用.
的应用.(1)请写出复数
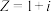 的三角形式,并利用泰勒展开式估算出
的三角形式,并利用泰勒展开式估算出 的3阶近似值(精确到0.001);
的3阶近似值(精确到0.001);(2)请根据上述材料证明欧拉公式,并计算
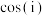 与
与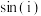 ;
;(3)记
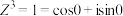 ,由棣莫弗定理得
,由棣莫弗定理得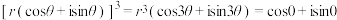 ,从而得
,从而得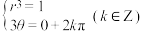 ,复数
,复数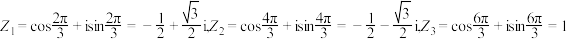 ,我们称其为1在复数域内的三次方根. 若
,我们称其为1在复数域内的三次方根. 若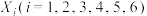 为64在复数域内的6次方根.求
为64在复数域内的6次方根.求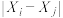 取值构成的集合,其中
取值构成的集合,其中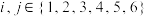 .
.
您最近一年使用:0次
名校
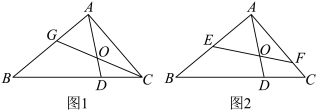
6 . 如图1所示,在 中,点
中,点 在线段
在线段 上,满足
上,满足 ,
, 是线段
是线段 上的点,且满足
上的点,且满足 ,线段
,线段 与线段
与线段 交于点
交于点 .
. ,求实数
,求实数 的值;
的值;
(2)若 ,求实数
,求实数 的值;
的值;
(3)如图2,过点 的直线与边
的直线与边 分别交于点
分别交于点 ,设
,设 ,
,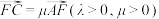 ;
;
(ⅰ)求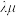 的最大值;
的最大值;
(ⅱ)设 的面积为
的面积为 ,四边形
,四边形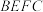 的面积为
的面积为 ,求
,求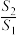 的取值范围.
的取值范围.
 中,点
中,点 在线段
在线段 上,满足
上,满足 ,
, 是线段
是线段 上的点,且满足
上的点,且满足 ,线段
,线段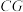 与线段
与线段 交于点
交于点 .
.
 ,求实数
,求实数 的值;
的值;(2)若
 ,求实数
,求实数 的值;
的值;(3)如图2,过点
 的直线与边
的直线与边 分别交于点
分别交于点 ,设
,设 ,
,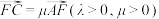 ;
;(ⅰ)求
 的最大值;
的最大值;(ⅱ)设
 的面积为
的面积为 ,四边形
,四边形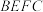 的面积为
的面积为 ,求
,求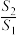 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
7 . 青岛胶东国际机场的显著特点之一是弯曲曲线的运用,衡量曲线弯曲程度的重要指标是曲率.考察图所示的光滑曲线 上的曲线段
上的曲线段 ,其弧长为
,其弧长为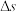 ,当动点从A沿曲线段
,当动点从A沿曲线段 运动到B点时,A点的切线
运动到B点时,A点的切线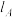 也随着转动到B点的切线
也随着转动到B点的切线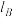 ,记这两条切线之间的夹角为
,记这两条切线之间的夹角为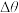 (它等于
(它等于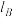 的倾斜角与
的倾斜角与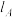 的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义
的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义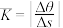 为曲线段
为曲线段 的平均曲率;显然当B越接近A,即
的平均曲率;显然当B越接近A,即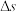 越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义曲线
越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义曲线 在点
在点 处的曲率计算公式为
处的曲率计算公式为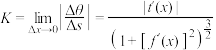 ,其中
,其中 .
. 的圆弧的平均曲率;
的圆弧的平均曲率;
(2)已知函数 ,求曲线
,求曲线 的曲率的最大值;
的曲率的最大值;
(3)已知函数 ,若
,若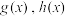 曲率为0时x的最小值分别为
曲率为0时x的最小值分别为 ,求证:
,求证: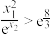 .
.
 上的曲线段
上的曲线段 ,其弧长为
,其弧长为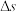 ,当动点从A沿曲线段
,当动点从A沿曲线段 运动到B点时,A点的切线
运动到B点时,A点的切线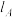 也随着转动到B点的切线
也随着转动到B点的切线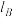 ,记这两条切线之间的夹角为
,记这两条切线之间的夹角为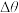 (它等于
(它等于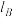 的倾斜角与
的倾斜角与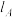 的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义
的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义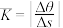 为曲线段
为曲线段 的平均曲率;显然当B越接近A,即
的平均曲率;显然当B越接近A,即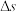 越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义曲线
越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义曲线 在点
在点 处的曲率计算公式为
处的曲率计算公式为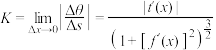 ,其中
,其中 .
.
 的圆弧的平均曲率;
的圆弧的平均曲率;(2)已知函数
 ,求曲线
,求曲线 的曲率的最大值;
的曲率的最大值;(3)已知函数
 ,若
,若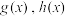 曲率为0时x的最小值分别为
曲率为0时x的最小值分别为 ,求证:
,求证: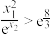 .
.
您最近一年使用:0次
2024-05-07更新
|
426次组卷
|
2卷引用:重庆市乌江新高考协作体2024届高考模拟监测(一)数学试题
名校
解题方法
8 . 已知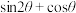 与
与 都是非零有理数,则在
都是非零有理数,则在 ,
, ,
, 中,一定是有理数的有( )个.
中,一定是有理数的有( )个.
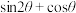 与
与 都是非零有理数,则在
都是非零有理数,则在 ,
, ,
, 中,一定是有理数的有( )个.
中,一定是有理数的有( )个.| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
2024-05-07更新
|
359次组卷
|
2卷引用:重庆市乌江新高考协作体2024届高考模拟监测(一)数学试题
名校
解题方法
9 . 柏拉图实体,也称为柏拉图多面体,是一组具有高度对称性的几何体.它们的特点是每个面都是相同的正多边形,每个顶点处的面的排列也完全相同.正八面体就是柏拉图实体的一种.如图是一个棱长为2的正八面体 .甲、乙二人使用它作游戏:甲任选三个顶点,乙任选三个面的中心点,构成三角形.甲、乙选择互不影响,下列说法正确的是( )
.甲、乙二人使用它作游戏:甲任选三个顶点,乙任选三个面的中心点,构成三角形.甲、乙选择互不影响,下列说法正确的是( )
 .甲、乙二人使用它作游戏:甲任选三个顶点,乙任选三个面的中心点,构成三角形.甲、乙选择互不影响,下列说法正确的是( )
.甲、乙二人使用它作游戏:甲任选三个顶点,乙任选三个面的中心点,构成三角形.甲、乙选择互不影响,下列说法正确的是( )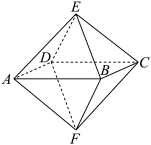
A.该正八面体的外接球的体积为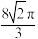 |
B.平面 截该正八面体的外接球所得截面的面积为 截该正八面体的外接球所得截面的面积为 |
C.甲能构成正三角形的概率为 |
D.甲与乙均能构成正三角形的概率为 |
您最近一年使用:0次
名校
解题方法
10 . 某项团体比赛分为两轮:第一轮由团队队员轮流与AI人工智能进行比赛.若挑战成功,参加第二轮攻擂赛与上任擂主争夺比赛胜利.现有甲队参加比赛,队中共3名事先排好顺序的队员参加挑战.
(1)第一轮与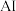 对战,比赛的规则如下:若某队员第一关闯关成功,则该队员继续闯第二关,否则该队员结束闯关并由下一位队员接力去闯第一关,若某队员第二关闯关成功,则该团队接力闯关活动结束,否则该成员结束闯关并由下一位队员接力去闯第二关;当第二关闯关成功或所有队员全部上场参加了闯关,该队挑战活动结束.已知甲队每位成员闯过第一关和第二关的概率分别为
对战,比赛的规则如下:若某队员第一关闯关成功,则该队员继续闯第二关,否则该队员结束闯关并由下一位队员接力去闯第一关,若某队员第二关闯关成功,则该团队接力闯关活动结束,否则该成员结束闯关并由下一位队员接力去闯第二关;当第二关闯关成功或所有队员全部上场参加了闯关,该队挑战活动结束.已知甲队每位成员闯过第一关和第二关的概率分别为 ,
, ,且每位成员闯关是否成功互不影响,每关结果也互不影响.用
,且每位成员闯关是否成功互不影响,每关结果也互不影响.用 表示甲队闯关活动结束时上场闯关的成员人数,求
表示甲队闯关活动结束时上场闯关的成员人数,求 的期望;
的期望;
(2)甲队已经顺利进入第二轮,现和擂主乙队 号队员进行比赛,规则为:双方先由1号队员比赛,负者被淘汰,胜者再与负方2号队员比赛
号队员进行比赛,规则为:双方先由1号队员比赛,负者被淘汰,胜者再与负方2号队员比赛 直到有一方队员全被淘汰,另一方获得胜利.已知,甲队三名队员
直到有一方队员全被淘汰,另一方获得胜利.已知,甲队三名队员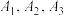 每场比赛的胜率分别为:
每场比赛的胜率分别为: ,
, ,
, ,若要求甲队获胜的概率大于
,若要求甲队获胜的概率大于 ,问
,问 是否满足?请说明理由.
是否满足?请说明理由.
(1)第一轮与
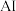 对战,比赛的规则如下:若某队员第一关闯关成功,则该队员继续闯第二关,否则该队员结束闯关并由下一位队员接力去闯第一关,若某队员第二关闯关成功,则该团队接力闯关活动结束,否则该成员结束闯关并由下一位队员接力去闯第二关;当第二关闯关成功或所有队员全部上场参加了闯关,该队挑战活动结束.已知甲队每位成员闯过第一关和第二关的概率分别为
对战,比赛的规则如下:若某队员第一关闯关成功,则该队员继续闯第二关,否则该队员结束闯关并由下一位队员接力去闯第一关,若某队员第二关闯关成功,则该团队接力闯关活动结束,否则该成员结束闯关并由下一位队员接力去闯第二关;当第二关闯关成功或所有队员全部上场参加了闯关,该队挑战活动结束.已知甲队每位成员闯过第一关和第二关的概率分别为 ,
, ,且每位成员闯关是否成功互不影响,每关结果也互不影响.用
,且每位成员闯关是否成功互不影响,每关结果也互不影响.用 表示甲队闯关活动结束时上场闯关的成员人数,求
表示甲队闯关活动结束时上场闯关的成员人数,求 的期望;
的期望;(2)甲队已经顺利进入第二轮,现和擂主乙队
 号队员进行比赛,规则为:双方先由1号队员比赛,负者被淘汰,胜者再与负方2号队员比赛
号队员进行比赛,规则为:双方先由1号队员比赛,负者被淘汰,胜者再与负方2号队员比赛 直到有一方队员全被淘汰,另一方获得胜利.已知,甲队三名队员
直到有一方队员全被淘汰,另一方获得胜利.已知,甲队三名队员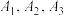 每场比赛的胜率分别为:
每场比赛的胜率分别为: ,
, ,
, ,若要求甲队获胜的概率大于
,若要求甲队获胜的概率大于 ,问
,问 是否满足?请说明理由.
是否满足?请说明理由.
您最近一年使用:0次



