名校
1 . 如图,矩形 中,
中, ,
, ,
, 为边
为边 的中点,沿
的中点,沿 将
将 折起,点
折起,点 折至
折至 处(
处(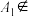 平面
平面 ),若
),若 为线段
为线段 的中点,平面
的中点,平面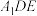 与平面
与平面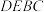 所成二面角
所成二面角 ,直线
,直线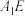 与平面
与平面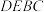 所成角为
所成角为 ,则在
,则在 折起的过程中,下列说法正确的是()
折起的过程中,下列说法正确的是()
 中,
中, ,
, ,
, 为边
为边 的中点,沿
的中点,沿 将
将 折起,点
折起,点 折至
折至 处(
处(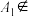 平面
平面 ),若
),若 为线段
为线段 的中点,平面
的中点,平面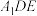 与平面
与平面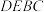 所成二面角
所成二面角 ,直线
,直线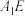 与平面
与平面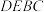 所成角为
所成角为 ,则在
,则在 折起的过程中,下列说法正确的是()
折起的过程中,下列说法正确的是()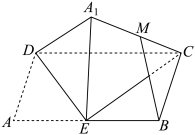
A.存在某个位置,使得 |
B. 面积的最大值为 面积的最大值为 |
C.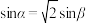 |
D.三棱锥 体积最大时,三棱锥 体积最大时,三棱锥 的外接球的表面积 的外接球的表面积 |
您最近一年使用:0次
名校
2 . 在通用技术课上,老师给同学们提供了一个如图所示的木质正四棱锥模型 ,点E在棱PB上,满足
,点E在棱PB上,满足 , 点F在棱PC上,满足
, 点F在棱PC上,满足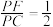
 要求同学们按照以下方案进行切割:
要求同学们按照以下方案进行切割: 平面
平面 ,并说明理由;
,并说明理由;
(2)过点A,E,F的平面α交PD于点H,沿平面α平将四棱锥模型切割成两部分,在实施过程中为了方便切割,需先在模型中确定H 点的位置;
①请求出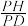 的值;
的值;
②若正四棱锥模型 的棱长均为6,求直线
的棱长均为6,求直线 与平面α所成角的正弦值.
与平面α所成角的正弦值.
 ,点E在棱PB上,满足
,点E在棱PB上,满足 , 点F在棱PC上,满足
, 点F在棱PC上,满足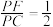
 要求同学们按照以下方案进行切割:
要求同学们按照以下方案进行切割: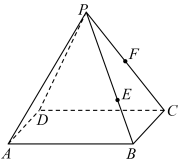
 平面
平面 ,并说明理由;
,并说明理由;(2)过点A,E,F的平面α交PD于点H,沿平面α平将四棱锥模型切割成两部分,在实施过程中为了方便切割,需先在模型中确定H 点的位置;
①请求出
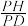 的值;
的值;②若正四棱锥模型
 的棱长均为6,求直线
的棱长均为6,求直线 与平面α所成角的正弦值.
与平面α所成角的正弦值.
您最近一年使用:0次
2024-06-28更新
|
506次组卷
|
2卷引用:广东省中山市中山纪念中学等五校2023-2024学年高一下学期第一次联考数学试卷
解题方法
3 . 如图,正方体 的棱长为
的棱长为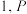 为
为 的中点,
的中点, 为线段
为线段 上的动点,过点
上的动点,过点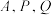 的平面截该正方体所得截面记为
的平面截该正方体所得截面记为 ,则下列命题正确的是( )
,则下列命题正确的是( )
 的棱长为
的棱长为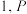 为
为 的中点,
的中点, 为线段
为线段 上的动点,过点
上的动点,过点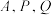 的平面截该正方体所得截面记为
的平面截该正方体所得截面记为 ,则下列命题正确的是( )
,则下列命题正确的是( )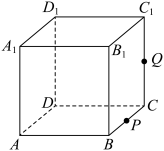
A.直线 与直线 与直线 所成角的正切值为 所成角的正切值为 |
B.当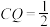 时, 时, 为等腰梯形 为等腰梯形 |
C.当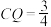 时, 时, 与 与 交于点 交于点 ,则 ,则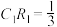 |
D.当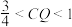 时, 时, 为四边形 为四边形 |
您最近一年使用:0次
4 . 如图所示,正四棱台 两底面的边长分别为4和8.
两底面的边长分别为4和8. ,求该四棱台的表面积;
,求该四棱台的表面积;
(2)若其侧面积等于两底面面积之和,求该四棱台的体积.
 两底面的边长分别为4和8.
两底面的边长分别为4和8.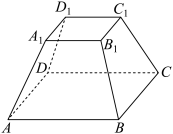
 ,求该四棱台的表面积;
,求该四棱台的表面积;(2)若其侧面积等于两底面面积之和,求该四棱台的体积.
您最近一年使用:0次
名校
5 . 已知向量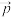 在基底
在基底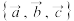 下的坐标是
下的坐标是 ,则
,则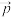 在基底
在基底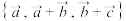 下的坐标为( )
下的坐标为( )
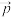 在基底
在基底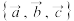 下的坐标是
下的坐标是 ,则
,则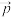 在基底
在基底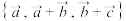 下的坐标为( )
下的坐标为( )A. | B.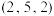 | C.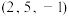 | D.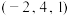 |
您最近一年使用:0次
2024-06-26更新
|
1187次组卷
|
8卷引用:广东省珠海市第二中学2024-2025学年高二上学期第一阶段考考试数学试题
广东省珠海市第二中学2024-2025学年高二上学期第一阶段考考试数学试题安徽省芜湖市第十二中学2021-2022学年高二上学期期中考试数学试卷(已下线)1.2空间向量基本定理——课后作业(基础版)吉林省长春市部分校2023-2024学年高一下学期期末测试数学试卷(已下线)数学01(全国通用)-新高二上学期数学开学摸底考试卷山东省济宁市邹城市北大新世纪高级中学2024-2025学年高二上学期开学考试数学试题福建省部分优质高中2024-2025学年高二上学期开学考试数学试卷(已下线)核心考点1 空间向量的运算 B提升卷 (高二期中考试必考的核心考点)
名校
解题方法
6 . 如图,在平行六面体 中,底面
中,底面 是边长为
是边长为 的正方形,侧棱
的正方形,侧棱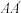 的长为
的长为 ,且
,且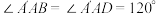 .求:
.求: 的长;
的长;
(2)直线 与
与 所成角的余弦值.
所成角的余弦值.
 中,底面
中,底面 是边长为
是边长为 的正方形,侧棱
的正方形,侧棱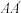 的长为
的长为 ,且
,且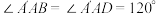 .求:
.求: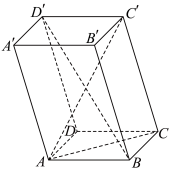
 的长;
的长;(2)直线
 与
与 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
2024-06-26更新
|
1829次组卷
|
12卷引用:广东省广州中学2021-2022学年高二上学期期中数学试题
广东省广州中学2021-2022学年高二上学期期中数学试题广东省广州市第六十五中学2023-2024学年高二上学期10月学情检测数学试题人教A版(2019) 选择性必修第一册 新高考名师导学 第一章 复习参考题 1(已下线)复习参考题 1人教A版(2019)选择性必修第一册课本习题第一章复习参考题河南省许昌市建安区第一高级中学2023-2024学年高二上学期10月月考数学试题四川省眉山市青神县青神中学校2023-2024学年高二上学期期中数学试题重庆市长寿区八校联考2023-2024学年高二上学期期末检测数学试题(B卷)(已下线)期末押题卷01(考试范围:苏教版2019选择性必修第二册)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第02讲 空间向量的数量积运算-【暑假预科讲义】(人教A版2019选择性必修第一册)(已下线)1.1空间向量及其运算——课堂例题山西省晋中市榆次区山西现代双语学校南校2024-2025学年高二上学期10月月考数学试题
23-24高二下·江苏·课前预习
名校
7 . 已知平行六面体 ,化简下列向量表达式,并在图中标出化简得到的向量:
,化简下列向量表达式,并在图中标出化简得到的向量: ;
;
(2) ;
;
(3) .
.
 ,化简下列向量表达式,并在图中标出化简得到的向量:
,化简下列向量表达式,并在图中标出化简得到的向量: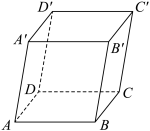
 ;
;(2)
 ;
;(3)
 .
.
您最近一年使用:0次
2024-06-25更新
|
1798次组卷
|
6卷引用:广东省深圳市桃源居中澳实验学校2024-2025学年高二上学期第一次月考数学试卷
广东省深圳市桃源居中澳实验学校2024-2025学年高二上学期第一次月考数学试卷(已下线)第六章 空间向量与立体几何(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)第一章 空间向量与立体几何全章综合检测卷-【暑假预科讲义】(人教A版2019选择性必修第一册)(已下线)第01讲 空间向量及其线性运算-【暑假预科讲义】(人教A版2019选择性必修第一册)(已下线)1.1空间向量及其运算——课堂例题(已下线)1.1.1 空间向量及其运算——课后作业(巩固版)
24-25高一上·全国·假期作业
8 . 已知平行六面体 ,则下列四式中错误的是( )
,则下列四式中错误的是( )
 ,则下列四式中错误的是( )
,则下列四式中错误的是( )A. |
B.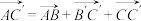 |
C. |
D. |
您最近一年使用:0次
名校
9 . 如图,在棱长为2的正方体 中,已知
中,已知 ,
, ,
, 分别是棱
分别是棱 ,
, ,
, 的中点,
的中点, 为平面
为平面 上的动点,且直线
上的动点,且直线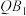 与直线
与直线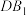 的夹角为
的夹角为 ,则点
,则点 的轨迹长度为( )
的轨迹长度为( )
 中,已知
中,已知 ,
, ,
, 分别是棱
分别是棱 ,
, ,
, 的中点,
的中点, 为平面
为平面 上的动点,且直线
上的动点,且直线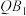 与直线
与直线 的夹角为
的夹角为 ,则点
,则点 的轨迹长度为( )
的轨迹长度为( )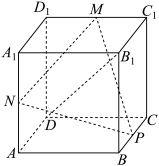
A.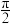 | B. | C.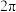 | D. |
您最近一年使用:0次
2024-06-25更新
|
882次组卷
|
8卷引用:广东省汕头市潮阳中英文学校2024-2025学年高二上学期9月月考数学试题
广东省汕头市潮阳中英文学校2024-2025学年高二上学期9月月考数学试题东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)2023-2024学年高三下学期第四次联合模拟考数学试题(已下线)拔高点突破02 立体几何中的动态、轨迹问题(六大题型)山东省百师联盟2024-2025学年高二上学期9月联考数学试题河南省周口市周口学校2024-2025学年高二上学期9月月考数学试题山西省阳泉市第一中学校2024-2025学年高二上学期10月月考数学试题(已下线)全真综合模拟卷(三)(高三大一轮好卷)(复盘卷)河南省郑州文华高级中学2024-2025学年高二上学期第一次月考数学试题
名校
解题方法
10 . 如图,在正方体 中,
中, 为
为 的中点.
的中点.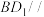 平面
平面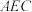 ;
;
(2) 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 平面
平面 ,若存在,请说明理由.
,若存在,请说明理由.
 中,
中, 为
为 的中点.
的中点.
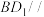 平面
平面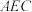 ;
;(2)
 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 平面
平面 ,若存在,请说明理由.
,若存在,请说明理由.
您最近一年使用:0次
2024-06-24更新
|
542次组卷
|
34卷引用:广东省汕头市潮阳实验学校2023-2024学年高一下学期期中考试数学试题
广东省汕头市潮阳实验学校2023-2024学年高一下学期期中考试数学试题湖南省长沙市第二十一中学2021-2022学年高一上学期期中数学试题山西省大同市第二中学校2021-2022学年高一下学期期中数学试题河南省商丘市宁陵县高级中学2021-2022学年高一下学期第二次月考数学试卷(B)(已下线)第47讲 直线与平面、平面与平面平行(已下线)8.5.3 平面与平面平行 (精讲)(1)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)8.5.3 平面与平面平行(精讲)-【题型分类归纳】2022-2023学年高一数学同步讲与练(人教A版2019必修第二册)专题6.3 空间中的平行关系-2021-2022学年高一数学北师大版2019必修第二册陕西省西安市西北工业大学附属中学2022-2023学年高一下学期期中数学试题(已下线)第03讲 空间中平行、垂直问题10种常见考法归类(1)(已下线)第03讲 空间中平行、垂直问题10种常见考法归类(2)广西百色市2022-2023学年高一下学期数学期末考试模拟试题(已下线)10.4 平面与平面间的位置关系(第1课时)(七大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)(已下线)考点巩固卷17 空间中的平行与垂直(八大考点)甘肃省兰州市兰州新区兰州新区高级中学2022-2023学年高一下学期期末数学试题(已下线)专题6-3立体几何大题综合归类-2(已下线)13.2.4 平面与平面的位置关系(1)-【帮课堂】(苏教版2019必修第二册)(已下线)高一下学期期中复习解答题压轴题十八大题型专练(2)-举一反三系列(人教A版2019必修第二册)河南省新乡市封丘县第一中学2023-2024学年高一下学期期中数学试题(已下线)专题19 平面与平面平行-《重难点题型·高分突破》(人教A版2019必修第二册)(已下线)8.5空间直线、平面的平行——随堂检测(已下线)专题05 空间直线﹑平面的平行-《知识解读·题型专练》(人教A版2019必修第二册)(已下线)8.5.3 平面与平面平行-同步题型分类归纳讲与练(人教A版2019必修第二册)四川省攀枝花市第三高级中学2023-2024高一下学期第二次月考数学试题(已下线)6.4.2平面与平面平行-【帮课堂】(北师大版2019必修第二册)(已下线)专题突破:空间几何体的动点探究问题-同步题型分类归纳讲与练(人教A版2019必修第二册)(已下线)核心考点5 立体几何中的位置关系 B提升卷 (高一期末考试必考的10大核心考点)广西壮族自治区河池市十校联体2023-2024学年高一下学期第二次联考(5月)数学试题云南省保山市智源中学2023-2024学年高一下学期4月期中数学试题山西省朔州市怀仁市第一中学校2023-2024学年高一下学期期中考试数学试题云南省昆明市第三中学2023-2024学年高一下学期期中考试数学试卷山东省济南市济阳闻韶中学2023-2024年高一下学期期中考试数学试题江西省宜春市丰城中学2023届高三上学期10月月考文科数学试题黑龙江省哈尔滨市宾县第二中学2022-2023学年高二上学期开学考试数学试题



