名校
1 . 给出定义:若 ,则称
,则称 为离实数
为离实数 最近的整数,记作
最近的整数,记作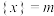 .在此基础上给出下列关于函数
.在此基础上给出下列关于函数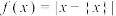 的四个结论,其中正确的是( )
的四个结论,其中正确的是( )
 ,则称
,则称 为离实数
为离实数 最近的整数,记作
最近的整数,记作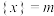 .在此基础上给出下列关于函数
.在此基础上给出下列关于函数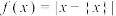 的四个结论,其中正确的是( )
的四个结论,其中正确的是( )A.函数 的定义域为R,值域为 的定义域为R,值域为 |
B.函数 的图象关于直线 的图象关于直线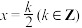 对称 对称 |
C.函数 是偶函数 是偶函数 |
D.函数 在 在 上单调递增 上单调递增 |
您最近半年使用:0次
2022-08-08更新
|
1059次组卷
|
9卷引用:福建省泉州市第七中学2022-2023学年高一上学期期中考试数学试题
福建省泉州市第七中学2022-2023学年高一上学期期中考试数学试题浙江省宁波市鄞州中学2022-2023学年高一上学期期中数学试题安徽省安庆市怀宁县新安中学2023-2024学年高一上学期期中考试数学试题北师大版(2019) 必修第一册 名校名师卷 专题三 函数江苏省连云港市灌南高级中学2022-2023学年高一上学期解题能力大赛数学试题(已下线)第3章 函数概念与性质(基础、典型、新文化、易错、压轴)专项训练-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)湖北省荆州市沙市中学2023-2024学年高一上学期10月月考数学试题广东省中山市龙山中学2023-2024学年高一上学期10月月考数学试题河北省邯郸市永年区第二中学2023-2024学年高一上学期12月月考数学试题
名校
解题方法
2 . 下列说法正确的是( )
A.若函数 的定义域为 的定义域为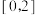 ,则函数 ,则函数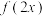 的定义域为 的定义域为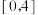 |
B.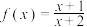 图象关于点 图象关于点 成中心对称 成中心对称 |
C.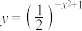 的最大值为 的最大值为 |
D.幂函数 在 在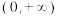 上为减函数,则 上为减函数,则 的值为 的值为 |
您最近半年使用:0次
2022-09-28更新
|
1914次组卷
|
10卷引用:福建省石狮市第八中学2021-2022学年高一上学期期中考试数学试题
福建省石狮市第八中学2021-2022学年高一上学期期中考试数学试题湖北省武汉市2022-2023学年高一上学期期中模拟(二)数学试题浙江省宁波市第四中学2022-2023学年高一上学期期中数学试题广东省东莞市东莞实验中学2022-2023学年高一上学期11月期中考试数学试题河北省石家庄二中实验学校2022-2023学年高一上学期期中数学试题广东省惠州仲恺高新区华实高级中学2023-2024学年高一上学期期中数学试题海南省海口市海南昌茂花园学校2023届高三上学期第二次月考数学试题第四章 指数函数、对数函数与幂函数(B卷·能力提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教B版2019必修第二册)第六章 幂函数、指数函数和对数函数(A卷·基础提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(苏教版2019必修第一册)辽宁省沈阳市五校协作体2022-2023学年高二下学期期末联考数学试题
名校
3 . 设函数 的定义域为
的定义域为 ,
,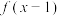 为奇函数,
为奇函数,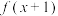 为偶函数,当
为偶函数,当 时,
时, ,则下列结论正确的是( )
,则下列结论正确的是( )
 的定义域为
的定义域为 ,
,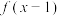 为奇函数,
为奇函数,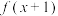 为偶函数,当
为偶函数,当 时,
时, ,则下列结论正确的是( )
,则下列结论正确的是( )A.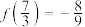 | B. 在 在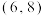 上为减函数 上为减函数 |
C.点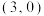 是函数 是函数 的一个对称中心 的一个对称中心 | D.方程 仅有 仅有 个实数解 个实数解 |
您最近半年使用:0次
2022-04-25更新
|
1518次组卷
|
8卷引用:福建省福州第十五中学2022-2023学年高一下学期期中适应性练习数学试题
名校
解题方法
4 . 定义在R上的奇函数 满足
满足 ,且当
,且当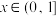 时,
时, ,则( )
,则( )
 满足
满足 ,且当
,且当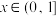 时,
时, ,则( )
,则( )A. 是周期函数 是周期函数 | B. 在(-1,1)上单调递减 在(-1,1)上单调递减 |
C. 的图象关于直线 的图象关于直线 对称 对称 | D. 的图象关于点(2,0)对称 的图象关于点(2,0)对称 |
您最近半年使用:0次
2022-03-11更新
|
1038次组卷
|
8卷引用:福建省泉州市第六中学2021-2022学年高二下学期期中模块测试数学试题
福建省泉州市第六中学2021-2022学年高二下学期期中模块测试数学试题福建省厦门市2022届高三毕业班3月第二次质量检测数学试题(已下线)三轮冲刺卷06-【赢在高考·黄金20卷】备战2022年高考数学模拟卷(新高考专用)海南省海口市海口中学2021-2022学年高二下学期期末考试数学试题(B卷)湖北省襄阳市南漳县第二中学2022-2023学年高三上学期9月月考数学试题湖南省长沙市长郡湘府中学2022-2023学年高二下学期数学竞赛试题江苏省南通市海安市实验中学2023-2024学年高三上学期10月月考数学试题(已下线)专题09 函数与导数(解密讲义)
名校
5 . 已知函数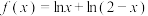 ,则( )
,则( )
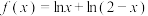 ,则( )
,则( )A. 在 在 上单调递增 上单调递增 | B. 在 在 上单调递增 上单调递增 |
C. 的图象关于直线 的图象关于直线 对称 对称 | D. 的值域为 的值域为 |
您最近半年使用:0次
2021-12-20更新
|
782次组卷
|
2卷引用:福建省建瓯市芝华中学2021-2022学年高一上学期期中考试数学试题
解题方法
6 . 写出一个同时具有下列性质①②③的函数 的解析式为
的解析式为
____________ .
①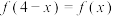 ;②当
;②当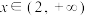 时,
时,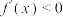 ;③
;③ 的最大值大于1.
的最大值大于1.
 的解析式为
的解析式为
①
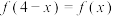 ;②当
;②当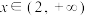 时,
时,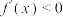 ;③
;③ 的最大值大于1.
的最大值大于1.
您最近半年使用:0次
2021-12-16更新
|
734次组卷
|
3卷引用:福建省永春美岭中学2021-2022学年高二下学期期中测试数学试题
福建省永春美岭中学2021-2022学年高二下学期期中测试数学试题辽宁省名校联盟2021-2022学年高三上学期12月份联合考试数学试题(已下线)第5章 导数及其应用 章末题型训练-《讲亮点》2021-2022学年高二数学新教材同步配套讲练(苏教版2019选择性必修第一册)
名校
7 . 下列命题中真命题的是( )
A.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
B.若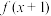 是偶函数,则 是偶函数,则 的图像关于直线 的图像关于直线 轴对称 轴对称 |
C.若 ,则 ,则 的图像关于点 的图像关于点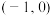 中心对称 中心对称 |
D. ,使得方程 ,使得方程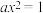 有解的充要条件是 有解的充要条件是 |
您最近半年使用:0次
2021-11-27更新
|
304次组卷
|
2卷引用:福建省福州市第一中学2021-2022学年高一上学期期中考试数学试题
名校
8 . 已知函数 , 则函数具有下列性质( )
, 则函数具有下列性质( )
 , 则函数具有下列性质( )
, 则函数具有下列性质( )A.函数 的图象关于点 的图象关于点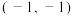 对称 对称 | B.函数 在 在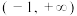 上单调递增 上单调递增 |
C.函数 的图象过原点 的图象过原点 | D.函数 的值域为 的值域为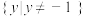 |
您最近半年使用:0次
2021-11-27更新
|
515次组卷
|
3卷引用:福建省福州市福清市高中联合体2021-2022学年高一上学期期中考试数学试题
名校
9 . 已知函数 ,则( )
,则( )
 ,则( )
,则( )A.当 时, 时, 是 是 上的减函数 上的减函数 |
B.当 时, 时, 的最大值为 的最大值为 |
C. 可能有两个极值点 可能有两个极值点 |
D.当 时,存在实数 时,存在实数 、 、 ,使得 ,使得 关于点 关于点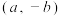 对称 对称 |
您最近半年使用:0次
2021-10-11更新
|
411次组卷
|
4卷引用:福建省莆田市莆田第二中学2022届高三上学期期中考数学试题
名校
解题方法
10 . 已知函数 对任意
对任意 都有
都有 ,若函数
,若函数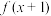 的图像关于
的图像关于 对称,且对任意的
对称,且对任意的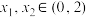 ,且
,且 ,都有
,都有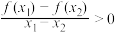 ,若
,若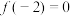 ,则下列结论正确的是( )
,则下列结论正确的是( )
 对任意
对任意 都有
都有 ,若函数
,若函数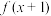 的图像关于
的图像关于 对称,且对任意的
对称,且对任意的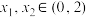 ,且
,且 ,都有
,都有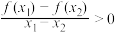 ,若
,若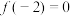 ,则下列结论正确的是( )
,则下列结论正确的是( )A. 是偶函数 是偶函数 | B.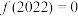 |
C. 的图像关于 的图像关于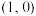 对称 对称 | D.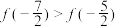 |
您最近半年使用:0次
2021-10-08更新
|
880次组卷
|
3卷引用:福建省罗源县协作校联考2021-2022学年高一上学期期中考试数学试题



