解题方法
1 . 下列函数在其定义域内既是奇函数又是增函数的是( )
A.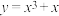 | B. | C. | D. |
您最近一年使用:0次
名校
2 . 已知函数 ,若
,若 ,
, ,且
,且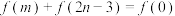 ,则
,则 最小值是
最小值是______ .
 ,若
,若 ,
, ,且
,且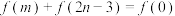 ,则
,则 最小值是
最小值是
您最近一年使用:0次
名校
解题方法
3 . 函数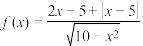 的奇偶性是
的奇偶性是_______ (从“奇函数”、“偶函数”、“既奇又偶”、“非奇非偶”中选一个恰当答案填入).
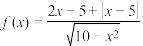 的奇偶性是
的奇偶性是
您最近一年使用:0次
7日内更新
|
275次组卷
|
2卷引用:河北省石家庄一中实验学校2024-2025学年高三上学期第一次考试数学试题
名校
解题方法
4 . 下列函数是偶函数的是( )
A.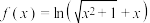 | B.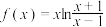 |
C. | D.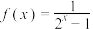 |
您最近一年使用:0次
解题方法
5 . 已知函数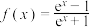 ,且满足
,且满足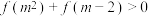 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
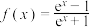 ,且满足
,且满足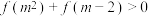 ,则实数
,则实数 的取值范围是( )
的取值范围是( )A. | B.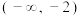 | C.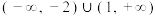 | D.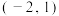 |
您最近一年使用:0次
7日内更新
|
803次组卷
|
2卷引用:2025届贵州市贵阳七校联盟高三上学期第一次联考数学试卷
2024高三·全国·专题练习
名校
解题方法
6 . 若函数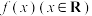 是奇函数,函数
是奇函数,函数 是偶函数,则( )
是偶函数,则( )
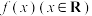 是奇函数,函数
是奇函数,函数 是偶函数,则( )
是偶函数,则( )A.函数 是奇函数 是奇函数 |
B.函数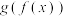 是奇函数 是奇函数 |
C.函数 是奇函数 是奇函数 |
D.函数 是奇函数 是奇函数 |
您最近一年使用:0次
7日内更新
|
783次组卷
|
3卷引用:【必夺分】突破点9 函数的奇偶性和周期性
(已下线)【必夺分】突破点9 函数的奇偶性和周期性湖南省长沙市明德中学2024-2025学年高二上学期10月阶段检测数学试卷陕西省咸阳市乾县杨汉中学2024-2025学年高二上学期第一次阶段性测试数学试卷
名校
解题方法
7 . 函数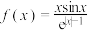 的部分图象大致为( )
的部分图象大致为( )
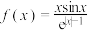 的部分图象大致为( )
的部分图象大致为( )A.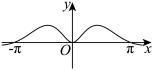 | B.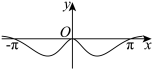 |
C.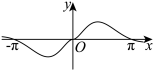 | D.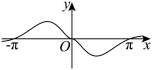 |
您最近一年使用:0次
7日内更新
|
374次组卷
|
2卷引用:安徽省六安市叶集皖西当代中学2024-2025学年高三上学期9月月考数学试题
名校
解题方法
8 . 函数 的部分图象大致为( )
的部分图象大致为( )
 的部分图象大致为( )
的部分图象大致为( )A. | B. |
C. | D. |
您最近一年使用:0次
7日内更新
|
1331次组卷
|
5卷引用:海南省2022-2023学年高三上学期高考全真模拟(二)数学试题
名校
解题方法
9 . 已知函数 的定义域为
的定义域为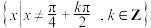 ,其导函数为
,其导函数为 ,
,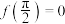 ,
,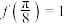 ,且
,且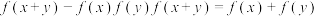 ,则( )
,则( )
 的定义域为
的定义域为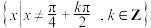 ,其导函数为
,其导函数为 ,
,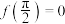 ,
,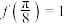 ,且
,且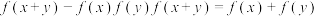 ,则( )
,则( )A.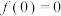 | B. 为奇函数 为奇函数 |
C.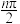 ( (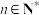 )是函数 )是函数 的周期 的周期 | D.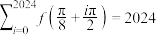 |
您最近一年使用:0次
名校
10 . 已知函数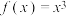 ,若正实数
,若正实数 ,
, 满足
满足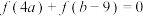 ,则
,则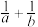 的最小值为( )
的最小值为( )
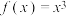 ,若正实数
,若正实数 ,
, 满足
满足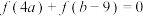 ,则
,则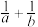 的最小值为( )
的最小值为( )| A.1 | B.3 | C.6 | D.9 |
您最近一年使用:0次
2024-10-15更新
|
344次组卷
|
2卷引用:四川省南充高级中学2024-2025学年高三上学期10月检测数学试题



