名校
解题方法
1 . 已知定义在 上的函数
上的函数 ,对任意
,对任意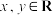 有
有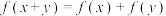 ,其中
,其中 ;当
;当 时,
时, ,则( )
,则( )
 上的函数
上的函数 ,对任意
,对任意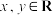 有
有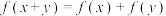 ,其中
,其中 ;当
;当 时,
时, ,则( )
,则( )A. 为 为 上的单调递增函数 上的单调递增函数 |
B. 为奇函数 为奇函数 |
C.若函数 为正比例函数,则函数 为正比例函数,则函数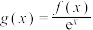 在 在 处取极小值 处取极小值 |
D.若函数 为正比例函数,则函数 为正比例函数,则函数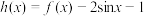 只有一个非负零点 只有一个非负零点 |
您最近一年使用:0次
名校
解题方法
2 . 下列四个函数中,不具有奇偶性的是( )
A. | B. |
C.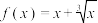 | D. |
您最近一年使用:0次
3 . 已知函数 ,
, ,则( )
,则( )
 ,
, ,则( )
,则( )A.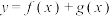 是偶函数 是偶函数 |
B.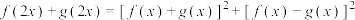 恒成立 恒成立 |
C.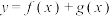 的值域是 的值域是 |
D.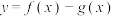 的值域是 的值域是 |
您最近一年使用:0次
解题方法
4 . 若函数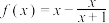 ,则下列函数中为奇函数的是( )
,则下列函数中为奇函数的是( )
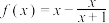 ,则下列函数中为奇函数的是( )
,则下列函数中为奇函数的是( )A.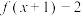 | B.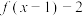 | C. | D. |
您最近一年使用:0次
昨日更新
|
672次组卷
|
3卷引用:2024届西藏自治区高三5月大联考理科数学试卷
2024届西藏自治区高三5月大联考理科数学试卷陕西省安康市安康市高新中学,安中分校2024届高三下学期5月模拟预测理科数学试题(已下线)第12讲 函数的奇偶性-【暑假自学课】(人教B版2019必修第一册)
解题方法
5 . 证明幂函数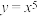 图象关于原点成中心对称.
图象关于原点成中心对称.
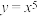 图象关于原点成中心对称.
图象关于原点成中心对称.
您最近一年使用:0次
解题方法
6 . 下列函数不是奇函数的是( )
A.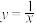 | B. | C. | D.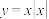 |
您最近一年使用:0次
解题方法
7 . 对于任意的 表示不超过
表示不超过 的最大整数.十八世纪,
的最大整数.十八世纪, 被“数学王子”高斯采用,因此得名为高斯函数,人们更习惯称为“取整函数”.下列说法正确的是( )
被“数学王子”高斯采用,因此得名为高斯函数,人们更习惯称为“取整函数”.下列说法正确的是( )
 表示不超过
表示不超过 的最大整数.十八世纪,
的最大整数.十八世纪, 被“数学王子”高斯采用,因此得名为高斯函数,人们更习惯称为“取整函数”.下列说法正确的是( )
被“数学王子”高斯采用,因此得名为高斯函数,人们更习惯称为“取整函数”.下列说法正确的是( )A.函数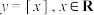 的图象关于原点对称 的图象关于原点对称 |
B.函数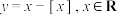 的值域为 的值域为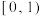 |
C.对于任意的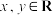 ,不等式 ,不等式 恒成立 恒成立 |
D.不等式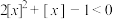 的解集为 的解集为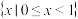 |
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
8 . 已知函数 的定义域为R,并且满足
的定义域为R,并且满足 ,
,
(1)求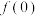 的值;
的值;
(2)判断函数的奇偶性并证明.
 的定义域为R,并且满足
的定义域为R,并且满足 ,
,(1)求
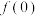 的值;
的值;(2)判断函数的奇偶性并证明.
您最近一年使用:0次
解题方法
9 . 已知函数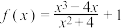 ,且
,且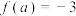 ,则
,则 ( )
( )
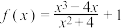 ,且
,且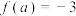 ,则
,则 ( )
( )| A.4 | B.5 | C.-4 | D.-3 |
您最近一年使用:0次
10 . 有以下6个函数:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤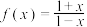 ;⑥
;⑥ .记事件
.记事件 为“从中任取的1个函数是奇函数”,事件
为“从中任取的1个函数是奇函数”,事件 为“从中任取的1个函数是偶函数”,事件
为“从中任取的1个函数是偶函数”,事件 的对立事件分别为
的对立事件分别为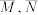 ,则( )
,则( )
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤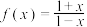 ;⑥
;⑥ .记事件
.记事件 为“从中任取的1个函数是奇函数”,事件
为“从中任取的1个函数是奇函数”,事件 为“从中任取的1个函数是偶函数”,事件
为“从中任取的1个函数是偶函数”,事件 的对立事件分别为
的对立事件分别为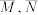 ,则( )
,则( )A. | B.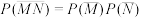 |
C.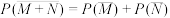 | D.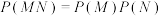 |
您最近一年使用:0次



