真题
1 . 记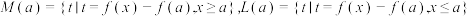
(1)若 ,求
,求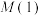 和
和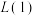 ;
;
(2)若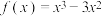 ,求证:对于任意
,求证:对于任意 ,都有
,都有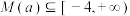 ,且存在
,且存在 ,使得
,使得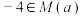 .
.
(3)已知定义在 上
上 有最小值,求证"
有最小值,求证" 是偶函数"的充要条件是“对于任意正实数
是偶函数"的充要条件是“对于任意正实数 ,均有
,均有 ”.
”.
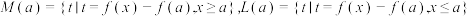
(1)若
 ,求
,求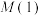 和
和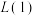 ;
;(2)若
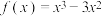 ,求证:对于任意
,求证:对于任意 ,都有
,都有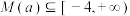 ,且存在
,且存在 ,使得
,使得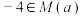 .
.(3)已知定义在
 上
上 有最小值,求证"
有最小值,求证" 是偶函数"的充要条件是“对于任意正实数
是偶函数"的充要条件是“对于任意正实数 ,均有
,均有 ”.
”.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
2 . (1)已知函数 ,
,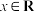 ,若
,若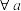 ,
,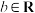 ,都有
,都有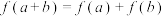 ,求证:
,求证: 为奇函数;
为奇函数;
(2)已知函数 ,
,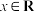 ,若
,若 ,
,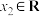 ,都有
,都有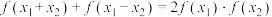 ,求证:
,求证: 为偶函数;
为偶函数;
(3)设函数 的定义域为
的定义域为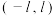 ,证明:
,证明: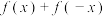 是偶函数,
是偶函数,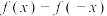 是奇函数.
是奇函数.
 ,
,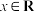 ,若
,若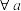 ,
,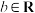 ,都有
,都有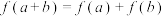 ,求证:
,求证: 为奇函数;
为奇函数;(2)已知函数
 ,
,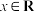 ,若
,若 ,
,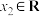 ,都有
,都有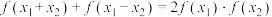 ,求证:
,求证: 为偶函数;
为偶函数;(3)设函数
 的定义域为
的定义域为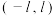 ,证明:
,证明: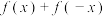 是偶函数,
是偶函数,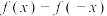 是奇函数.
是奇函数.
您最近一年使用:0次
3 . 设函数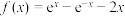 ,则不等式
,则不等式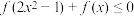 的解集为( ).
的解集为( ).
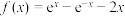 ,则不等式
,则不等式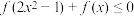 的解集为( ).
的解集为( ).A. | B. |
C. | D.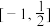 |
您最近一年使用:0次
2024-09-14更新
|
1130次组卷
|
3卷引用:新疆新和县实验中学2022-2023学年高三上学期第二次月考数学试题(文)
新疆新和县实验中学2022-2023学年高三上学期第二次月考数学试题(文)新疆新和县实验中学2022-2023学年高三上学期第二次月考数学试题(理)(已下线)2.3函数的奇偶性和周期性【同步课时】北京专版
名校
4 . 已知函数 与
与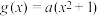 的图象恰有一个交点,则
的图象恰有一个交点,则 ( )
( )
 与
与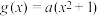 的图象恰有一个交点,则
的图象恰有一个交点,则 ( )
( )A. | B. | C.1 | D.2 |
您最近一年使用:0次
2024-09-13更新
|
606次组卷
|
4卷引用:贵州省遵义市桐梓县共同体联考2024-2025学年高三上学期9月月考数学试题
贵州省遵义市桐梓县共同体联考2024-2025学年高三上学期9月月考数学试题(已下线)考点19 函数的零点 --高考数学100个黄金考点(2025届)【讲】(已下线)考点19 函数的零点 --高考数学100个黄金考点(2025届)1【讲】湖南省邵阳市邵东市第一中学2024-2025学年高三上学期第三次月考(10月)数学试题
23-24高二下·全国·随堂练习
解题方法
5 . 若对于定义域内的任意一个 ,都有
,都有 ,则函数
,则函数 是奇函数.
是奇函数.( )
 ,都有
,都有 ,则函数
,则函数 是奇函数.
是奇函数.
您最近一年使用:0次
名校
解题方法
6 . 已知函数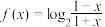 .
.
(1)判断并证明 的奇偶性;
的奇偶性;
(2)若对任意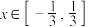 ,
, ,不等式
,不等式 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
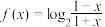 .
.(1)判断并证明
 的奇偶性;
的奇偶性;(2)若对任意
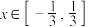 ,
, ,不等式
,不等式 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
您最近一年使用:0次
2024-09-12更新
|
2066次组卷
|
5卷引用:江苏省南通市2025届高三九月份调研考试数学试题
江苏省南通市2025届高三九月份调研考试数学试题安徽省六安第二中学2024-2025学年高三上学期第二次月考(10月)数学试题重庆市乌江新高考协作体2025届高三上学期高考质量调研(二)(10月)数学试题(已下线)4.2.3 对数函数的性质与图象+4.3 指数函数与对数函数的关系——课后作业(提升版)山东省聊城第一中学2025届高三上学期第一次月考数学试题
名校
7 . 已知函数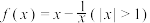 ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )
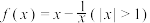 ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )A. 为奇函数 为奇函数 |
B. 在其定义域内为增函数 在其定义域内为增函数 |
C.曲线 上任意一点与 上任意一点与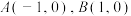 两点连线的斜率之和为定值 两点连线的斜率之和为定值 |
D.曲线 的切线的斜率的最大值为2 的切线的斜率的最大值为2 |
您最近一年使用:0次
名校
解题方法
8 . 下列函数既是奇函数,又在区间 上单调递减的是( )
上单调递减的是( )
 上单调递减的是( )
上单调递减的是( )A. | B. |
C.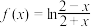 | D.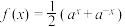 |
您最近一年使用:0次
2024-09-11更新
|
570次组卷
|
2卷引用:陕西省榆林市定边县第四中学2022-2023学年高三上学期第一次月考文科数学试题
名校
解题方法
9 . 已知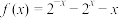 ,则
,则 的解集为
的解集为__________ .
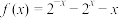 ,则
,则 的解集为
的解集为
您最近一年使用:0次
2024-09-10更新
|
2612次组卷
|
3卷引用:广东省深圳市红岭中学(红岭教育集团)2025届高三上学期第一次统一考试数学试卷
广东省深圳市红岭中学(红岭教育集团)2025届高三上学期第一次统一考试数学试卷(已下线)考点16 指数函数 --高考数学100个黄金考点(2025届)【练】上海市上海市实验学校2025届高三上学期9月练习数学试题
10 . 下列函数中,最小正周期为 且图象关于原点对称的函数是( )
且图象关于原点对称的函数是( )
 且图象关于原点对称的函数是( )
且图象关于原点对称的函数是( )A.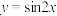 | B. | C. | D.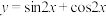 |
您最近一年使用:0次



