1 . 已知函数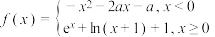 的值域为
的值域为 ,则
,则 的取值范围是( )
的取值范围是( )
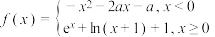 的值域为
的值域为 ,则
,则 的取值范围是( )
的取值范围是( )A. | B.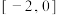 |
C.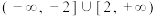 | D. |
您最近一年使用:0次
解题方法
2 . 已知函数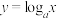 在
在 上是严格减函数,求函数
上是严格减函数,求函数 在
在 上的最值.
上的最值.
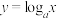 在
在 上是严格减函数,求函数
上是严格减函数,求函数 在
在 上的最值.
上的最值.
您最近一年使用:0次
7日内更新
|
77次组卷
|
2卷引用:【巩固卷】第5章测评卷 单元测试A-沪教版(2020)必修第一册
解题方法
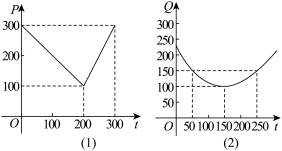
3 . 某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线表示.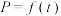 ;
;
(2)写出图(2)中表示的种植成本与时间的函数关系式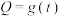 ;
;
(3)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
(注:市场售价和种植成本的单位:元/100kg,时间单位:天)
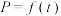 ;
;(2)写出图(2)中表示的种植成本与时间的函数关系式
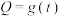 ;
;(3)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
(注:市场售价和种植成本的单位:元/100kg,时间单位:天)
您最近一年使用:0次
4 . 求函数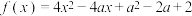 在
在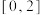 上的最小值.
上的最小值.
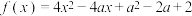 在
在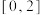 上的最小值.
上的最小值.
您最近一年使用:0次
解题方法
5 . 已知函数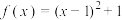 定义在区间
定义在区间 上,求
上,求 的最值.
的最值.
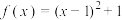 定义在区间
定义在区间 上,求
上,求 的最值.
的最值.
您最近一年使用:0次
解题方法
6 . 已知函数 ,
,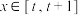 的最小值为
的最小值为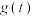 ,求
,求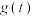 的表达式.
的表达式.
 ,
,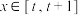 的最小值为
的最小值为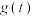 ,求
,求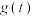 的表达式.
的表达式.
您最近一年使用:0次
解题方法
7 . 已知函数 ,求
,求 在
在 上的最大值与最小值.
上的最大值与最小值.
 ,求
,求 在
在 上的最大值与最小值.
上的最大值与最小值.
您最近一年使用:0次
解题方法
8 . 求函数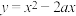 在区间
在区间 上的最小值.
上的最小值.
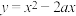 在区间
在区间 上的最小值.
上的最小值.
您最近一年使用:0次
名校
解题方法
9 . 已知函数 .
.
(1)若 ,求不等式
,求不等式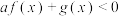 的解集;
的解集;
(2)若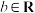 ,对
,对 ,使得
,使得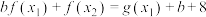 成立,求
成立,求 的取值范围.
的取值范围.
 .
.(1)若
 ,求不等式
,求不等式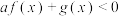 的解集;
的解集;(2)若
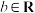 ,对
,对 ,使得
,使得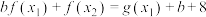 成立,求
成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-10更新
|
396次组卷
|
3卷引用:重庆市第八中学校2023-2024学年高二下学期期末考试数学试卷
重庆市第八中学校2023-2024学年高二下学期期末考试数学试卷重庆市西南大学附属中学校2023-2024学年高二下学期末考试数学试卷(已下线)周测2 一元二次函数、方程和不等式 一轮周测卷(提升卷)
名校
10 . 已知二次函数 满足
满足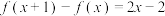 且
且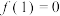 .
.
 的解析式;
的解析式;(2)设
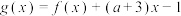 ,
, ,求函数
,求函数 的最小值
的最小值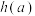 .
.
您最近一年使用:0次



