2024高三·全国·专题练习
解题方法
1 . 将连续正整数1,2, ,
, 从小到大排列构成一个数
从小到大排列构成一个数 ,
,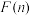 为这个数的位数
为这个数的位数 如当
如当 时,此数为123456789101112,共有15个数字,
时,此数为123456789101112,共有15个数字,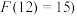 ,现从这个数中随机取一个数字,
,现从这个数中随机取一个数字, 为恰好取到0的概率.
为恰好取到0的概率.
(1)求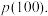
(2)当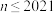 时,求
时,求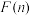 的表达式.
的表达式.
(3)令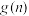 为这个数中数字0的个数,
为这个数中数字0的个数,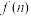 为这个数中数字9的个数,
为这个数中数字9的个数,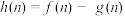 ,
,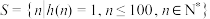 ,求当
,求当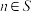 时
时 的最大值.
的最大值.
 ,
, 从小到大排列构成一个数
从小到大排列构成一个数 ,
,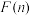 为这个数的位数
为这个数的位数 如当
如当 时,此数为123456789101112,共有15个数字,
时,此数为123456789101112,共有15个数字,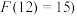 ,现从这个数中随机取一个数字,
,现从这个数中随机取一个数字, 为恰好取到0的概率.
为恰好取到0的概率.(1)求
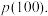
(2)当
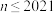 时,求
时,求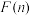 的表达式.
的表达式.(3)令
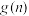 为这个数中数字0的个数,
为这个数中数字0的个数,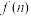 为这个数中数字9的个数,
为这个数中数字9的个数,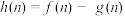 ,
,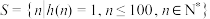 ,求当
,求当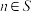 时
时 的最大值.
的最大值.
您最近一年使用:0次
解题方法
2 . 某班学生分A, ,
, ,
, 四组参加数学知识竞答,规则如下:四组之间进行单循环(每组均与另外三组进行一场比赛);每场比赛胜者积3分,负者0分;若出现平局,则比赛双方各积1分.现假设四个组战胜或者负于对手的概率均为
四组参加数学知识竞答,规则如下:四组之间进行单循环(每组均与另外三组进行一场比赛);每场比赛胜者积3分,负者0分;若出现平局,则比赛双方各积1分.现假设四个组战胜或者负于对手的概率均为 ,出现平局的概率为
,出现平局的概率为 ,每场比赛相互独立.
,每场比赛相互独立.
(1)求A组在参加两场比赛后得分为3分的概率;
(2)一轮单循环结束后,求四组总积分一样的情况种数,并计算四组总积分一样的概率.
 ,
, ,
, 四组参加数学知识竞答,规则如下:四组之间进行单循环(每组均与另外三组进行一场比赛);每场比赛胜者积3分,负者0分;若出现平局,则比赛双方各积1分.现假设四个组战胜或者负于对手的概率均为
四组参加数学知识竞答,规则如下:四组之间进行单循环(每组均与另外三组进行一场比赛);每场比赛胜者积3分,负者0分;若出现平局,则比赛双方各积1分.现假设四个组战胜或者负于对手的概率均为 ,出现平局的概率为
,出现平局的概率为 ,每场比赛相互独立.
,每场比赛相互独立.(1)求A组在参加两场比赛后得分为3分的概率;
(2)一轮单循环结束后,求四组总积分一样的情况种数,并计算四组总积分一样的概率.
您最近一年使用:0次
3 . 甲口袋中装有3个黑球和1个白球,乙口袋中装有3个白球.现同时从甲、乙两口袋中各任取一个球交换放入对方口袋,共进行了2次这样的操作后,甲口袋中恰有2个黑球的概率为
您最近一年使用:0次
2024-01-13更新
|
508次组卷
|
2卷引用:上海市南汇中学2023-2024学年高二上学期期末考试数学试卷
4 . 已知A袋内有大小相同的1个红球和3个白球,B袋内有大小相同的1个红球和2个白球.现从A、B两个袋内各任取1个球,则恰好有1个红球的概率为___________ .
您最近一年使用:0次
2024-01-13更新
|
357次组卷
|
3卷引用:山东省济宁市第一中学2023-2024学年高二上学期质量检测(三)数学试题
5 . 甲乙两人进行羽毛球比赛,在前三局比赛中,甲胜2局,乙胜1局,规定先胜3局者取得最终胜利,已知甲在每局比赛中获胜的概率为 ,乙在每局比赛中获胜的概率为
,乙在每局比赛中获胜的概率为 ,且各局比赛结果相互独立,则甲取得最终胜利的概率为( )
,且各局比赛结果相互独立,则甲取得最终胜利的概率为( )
 ,乙在每局比赛中获胜的概率为
,乙在每局比赛中获胜的概率为 ,且各局比赛结果相互独立,则甲取得最终胜利的概率为( )
,且各局比赛结果相互独立,则甲取得最终胜利的概率为( )A.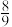 | B. | C.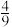 | D.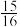 |
您最近一年使用:0次
2024-01-13更新
|
996次组卷
|
8卷引用:山东省济宁市第一中学2023-2024学年高二上学期质量检测(三)数学试题
山东省济宁市第一中学2023-2024学年高二上学期质量检测(三)数学试题山东省淄博市第七中学2023-2024学年高二上学期期末数学试题(已下线)专题18 条件概率5种常见考法归类-【寒假自学课】2024年高二数学寒假提升学与练(苏教版2019)河北省石家庄市西山学校2023-2024学年高二上学期期末数学试题(已下线)第十章 概率(知识归纳+题型突破)-单元速记·巧练(人教A版2019必修第二册)(已下线)8.1 条件概率(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第04讲 10.2 事件的相互独立性-【帮课堂】(人教A版2019必修第二册)(已下线)专题10 互斥事件与独立事件高频考点-《期末真题分类汇编》(江苏专用)
名校
解题方法
6 . 甲、乙两人准备进行羽毛球比赛,比赛规定:一回合中赢球的一方作为下一回合的发球方.若甲发球,则本回合甲赢的概率为 ,若乙发球,则本回合甲赢的概率为
,若乙发球,则本回合甲赢的概率为 ,每回合比赛的结果相互独立.经抽签决定,第1回合由甲发球.
,每回合比赛的结果相互独立.经抽签决定,第1回合由甲发球.
(1)求第4个回合甲发球的概率;
(2)设前4个回合中,甲发球的次数为 ,求
,求 的分布列及期望.
的分布列及期望.
 ,若乙发球,则本回合甲赢的概率为
,若乙发球,则本回合甲赢的概率为 ,每回合比赛的结果相互独立.经抽签决定,第1回合由甲发球.
,每回合比赛的结果相互独立.经抽签决定,第1回合由甲发球.(1)求第4个回合甲发球的概率;
(2)设前4个回合中,甲发球的次数为
 ,求
,求 的分布列及期望.
的分布列及期望.
您最近一年使用:0次
7 . 已知实数 的平均数为4,则这四个数的中位数的取值范围是
的平均数为4,则这四个数的中位数的取值范围是______ .
 的平均数为4,则这四个数的中位数的取值范围是
的平均数为4,则这四个数的中位数的取值范围是
您最近一年使用:0次
2023-11-24更新
|
667次组卷
|
8卷引用:上海市宜川中学2023-2024学年高三上学期期中考试数学试题
上海市宜川中学2023-2024学年高三上学期期中考试数学试题(已下线)第十章 综合测试B(提升卷)(已下线)专题05 统计与概率-【常考压轴题】上海市部分学校2023-2024学年高三下学期3月学科素养测试数学试卷(已下线)9.2.3?总体集中趋势的估计——课后作业(巩固版)上海市青浦区朱家角中学2023-2024学年高二下学期期中考试数学试题(已下线)第05讲 9.2.3 总体集中趋势的估计-【帮课堂】(人教A版2019必修第二册)(已下线)【练】专题四 概率统计中的范围与最值问题(压轴大全)
8 . 手工刺绣是中国非物质文化遗产之一,指以手工方式,用针和线把人的设计和制作添加在任何存在的织物上的一种艺术,大致分为绘制白描图和手工着色、电脑着色,选线、配线和裁布三个环节,简记为工序A,工序 ,工序
,工序 .经过试验测得小李在这三道工序成功的概率依次为
.经过试验测得小李在这三道工序成功的概率依次为 ,
, ,
, .现某单位推出一项手工刺绣体验活动,报名费30元,成功通过三道工序最终的奖励金额是200元,为了更好地激励参与者的兴趣,举办方推出了一项工序补救服务,可以在着手前付费聘请技术员,若某一道工序没有成功,可以由技术员完成本道工序.每位技术员只完成其中一道工序,每聘请一位技术员需另付费100元,制作完成后没有接受技术员补救服务的退还一半的聘请费用.
.现某单位推出一项手工刺绣体验活动,报名费30元,成功通过三道工序最终的奖励金额是200元,为了更好地激励参与者的兴趣,举办方推出了一项工序补救服务,可以在着手前付费聘请技术员,若某一道工序没有成功,可以由技术员完成本道工序.每位技术员只完成其中一道工序,每聘请一位技术员需另付费100元,制作完成后没有接受技术员补救服务的退还一半的聘请费用.
(1)若小李聘请一位技术员,求他成功完成三道工序的概率;
(2)若小李聘请两位技术员,求他最终获得收益的期望值.
 ,工序
,工序 .经过试验测得小李在这三道工序成功的概率依次为
.经过试验测得小李在这三道工序成功的概率依次为 ,
, ,
, .现某单位推出一项手工刺绣体验活动,报名费30元,成功通过三道工序最终的奖励金额是200元,为了更好地激励参与者的兴趣,举办方推出了一项工序补救服务,可以在着手前付费聘请技术员,若某一道工序没有成功,可以由技术员完成本道工序.每位技术员只完成其中一道工序,每聘请一位技术员需另付费100元,制作完成后没有接受技术员补救服务的退还一半的聘请费用.
.现某单位推出一项手工刺绣体验活动,报名费30元,成功通过三道工序最终的奖励金额是200元,为了更好地激励参与者的兴趣,举办方推出了一项工序补救服务,可以在着手前付费聘请技术员,若某一道工序没有成功,可以由技术员完成本道工序.每位技术员只完成其中一道工序,每聘请一位技术员需另付费100元,制作完成后没有接受技术员补救服务的退还一半的聘请费用.(1)若小李聘请一位技术员,求他成功完成三道工序的概率;
(2)若小李聘请两位技术员,求他最终获得收益的期望值.
您最近一年使用:0次
名校
解题方法
9 . 某校积极开展“戏曲进校园”活动,为了解该校各班参加戏曲兴趣小组的人数,从全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据.已知样本平均数为7,样本标准差为2,且样本数据互不相等,则该样本数据的极差为( )
| A.3 | B.4 | C.5 | D.6 |
您最近一年使用:0次
2023-09-06更新
|
1504次组卷
|
9卷引用:安徽省A10联盟2023-2024学年高二上学期9月初开学摸底考试数学试题
安徽省A10联盟2023-2024学年高二上学期9月初开学摸底考试数学试题(已下线)第十章 综合测试B(提升卷)(已下线)第二节 用样本的数字特征估计总体 B卷素养养成卷 一轮复习点点通(已下线)第十章 第二节 用样本的数字特征估计总体 一轮复习点点通(已下线)第5章 统计与概率-【优化数学】单元测试基础卷(人教B版2019)(已下线)第九章 统计(压轴题专练)-单元速记·巧练(人教A版2019必修第二册)单元测试B卷——第九章?统计(已下线)第9章 统计 单元综合检测(重难点)-《重难点题型·高分突破》(人教A版2019必修第二册)(已下线)核心考点9 统计 B提升卷 (高一期末考试必考的10大核心考点)
名校
解题方法
10 . 如图,一个质点在随机外力的作用下,从原点0出发,每隔1s等可能地向左或向右移动一个单位,则移动3次后质点位于1的位置的概率是( )


A. | B. | C.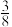 | D. |
您最近一年使用:0次



