名校
1 . 已知函数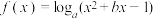 ,其中
,其中 且
且 .
.
(1)若 ,
, ,求不等式
,求不等式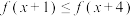 的解集;
的解集;
(2)若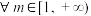 ,
,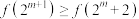 ,求b的取值范围.
,求b的取值范围.
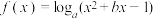 ,其中
,其中 且
且 .
.(1)若
 ,
, ,求不等式
,求不等式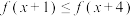 的解集;
的解集;(2)若
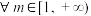 ,
,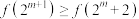 ,求b的取值范围.
,求b的取值范围.
您最近一年使用:0次
2023-12-23更新
|
310次组卷
|
4卷引用:贵州省六盘水市2023-2024学年高一上学期12月月考数学试题
名校
解题方法
2 . 已知函数 (
( 且
且 )是偶函数.
)是偶函数.
(1)求 的值;
的值;
(2)判断函数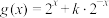 在
在 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)若 ,且
,且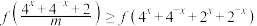 对
对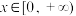 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 (
( 且
且 )是偶函数.
)是偶函数.(1)求
 的值;
的值;(2)判断函数
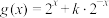 在
在 的单调性,并用定义证明;
的单调性,并用定义证明;(3)若
 ,且
,且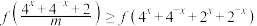 对
对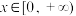 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2022-12-08更新
|
614次组卷
|
5卷引用:贵州省毕节市金沙县2022-2023学年高一上学期12月月考数学试题
解题方法
3 . 已知函数 .
.
(1)求函数 的定义域;
的定义域;
(2)解不等式: ;
;
(3)已知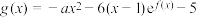 的图象在
的图象在 轴的上方,求实数
轴的上方,求实数 的取值范围.
的取值范围.
 .
.(1)求函数
 的定义域;
的定义域;(2)解不等式:
 ;
;(3)已知
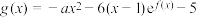 的图象在
的图象在 轴的上方,求实数
轴的上方,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2022-01-16更新
|
1972次组卷
|
5卷引用:贵州省黔西南州金成实验学校2023届高三上学期第一次月考数学试题
贵州省黔西南州金成实验学校2023届高三上学期第一次月考数学试题云南省昆明市官渡区2021-2022学年高一上学期期末考试数学试题第4章 指数概念与对数函数(基础、典型、易错、新文化、压轴)专项训练-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)(已下线)重难点03函数(15种解题模型与方法)(1)(已下线)专题16对数函数-【倍速学习法】(人教A版2019必修第一册)
解题方法
4 . 已知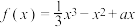
(1)若 在区间
在区间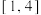 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)当 时,是否存在点
时,是否存在点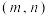 ,使得
,使得 的图像关于点
的图像关于点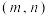 对称?若存在,求出点
对称?若存在,求出点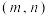 ,若不存在,请说明理由;
,若不存在,请说明理由;
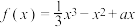
(1)若
 在区间
在区间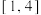 恒成立,求
恒成立,求 的取值范围;
的取值范围;(2)当
 时,是否存在点
时,是否存在点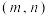 ,使得
,使得 的图像关于点
的图像关于点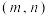 对称?若存在,求出点
对称?若存在,求出点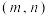 ,若不存在,请说明理由;
,若不存在,请说明理由;
您最近一年使用:0次
名校
5 . 已知二次函数 满足对任意
满足对任意 ,都有
,都有 ;
;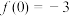 ;
; 的图象与
的图象与 轴的两个交点之间的距离为
轴的两个交点之间的距离为 .
.
(1)求 的解析式;
的解析式;
(2)记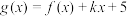 ,
,
(i)若 为单调函数,求
为单调函数,求 的取值范围;
的取值范围;
(ii)记 的最小值为
的最小值为 ,若方程
,若方程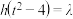 有两个不等的根,求
有两个不等的根,求 的取值范围.
的取值范围.
 满足对任意
满足对任意 ,都有
,都有 ;
;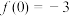 ;
; 的图象与
的图象与 轴的两个交点之间的距离为
轴的两个交点之间的距离为 .
.(1)求
 的解析式;
的解析式;(2)记
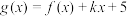 ,
,
(i)若
 为单调函数,求
为单调函数,求 的取值范围;
的取值范围;(ii)记
 的最小值为
的最小值为 ,若方程
,若方程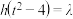 有两个不等的根,求
有两个不等的根,求 的取值范围.
的取值范围.
您最近一年使用:0次
2021-10-21更新
|
700次组卷
|
4卷引用:贵州省遵义市道真仡佬族苗族自治县民族高级中学2022-2023学年高二上学期第一次月考数学试题
贵州省遵义市道真仡佬族苗族自治县民族高级中学2022-2023学年高二上学期第一次月考数学试题四川省成都市树德中学2021-2022学年高一上学期10月阶段性测试数学试题海南省海口市海口中学2021-2022学年高一上学期期末考试数学试题(已下线)专题11 指数函数与对数函数压轴题型汇总-2021-2022学年高一《新题速递·数学》(人教A版2019)
解题方法
6 . 已知函数 (
( 为常数,且
为常数,且 ,
, ).请在下面四个函数:①
).请在下面四个函数:①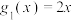 ,②
,② ,③
,③ ,④
,④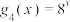 ,中选择一个函数作为
,中选择一个函数作为 ,使得
,使得 具有奇偶性.
具有奇偶性.
(1)请写出 表达式,并求
表达式,并求 的值;
的值;
(2)当 为奇函数时,若对任意的
为奇函数时,若对任意的 ,都有
,都有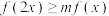 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(3)当 为偶函数时,请讨论关于
为偶函数时,请讨论关于 的方程
的方程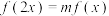 解的个数.
解的个数.
 (
( 为常数,且
为常数,且 ,
, ).请在下面四个函数:①
).请在下面四个函数:①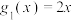 ,②
,② ,③
,③ ,④
,④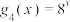 ,中选择一个函数作为
,中选择一个函数作为 ,使得
,使得 具有奇偶性.
具有奇偶性.(1)请写出
 表达式,并求
表达式,并求 的值;
的值;(2)当
 为奇函数时,若对任意的
为奇函数时,若对任意的 ,都有
,都有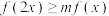 成立,求实数
成立,求实数 的取值范围;
的取值范围;(3)当
 为偶函数时,请讨论关于
为偶函数时,请讨论关于 的方程
的方程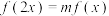 解的个数.
解的个数.
您最近一年使用:0次
2021-01-28更新
|
1610次组卷
|
4卷引用:贵州省六盘水市第四中学2023-2024学年高一下学期第一次月考数学试卷
贵州省六盘水市第四中学2023-2024学年高一下学期第一次月考数学试卷江苏省镇江市2020-2021学年高一上学期期末数学试题(已下线)专题8.3 函数应用 章末检测3(难)-【满分计划】2021-2022学年高一数学阶段性复习测试卷(苏教版2019必修第一册)(已下线)第四章测试题-2021-2022学年高一数学同步辅导讲义与检测(人教A版2019必修第一册)
解题方法
7 . 已知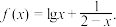
(1)求函数 的定义域;
的定义域;
(2)证明: 在
在 上为增函数;
上为增函数;
(3)当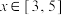 时,求函数的值域.
时,求函数的值域.
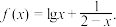
(1)求函数
 的定义域;
的定义域;(2)证明:
 在
在 上为增函数;
上为增函数;(3)当
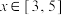 时,求函数的值域.
时,求函数的值域.
您最近一年使用:0次
8 . 已知二次函数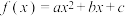 满足下列3个条件:
满足下列3个条件:
① 的图象过坐标原点;②对于任意
的图象过坐标原点;②对于任意 都有
都有 ;③对于任意
;③对于任意 都有
都有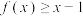 .
.
(1)求函数 的解析式;
的解析式;
(2)令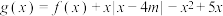 .(其中m为参数)
.(其中m为参数)
①求函数 的单调区间;
的单调区间;
②设 ,函数
,函数 在区间
在区间 上既有最大值又有最小值,请写出实数p,q的取值范围.(用m表示出p,q范围即可,不需要过程)
上既有最大值又有最小值,请写出实数p,q的取值范围.(用m表示出p,q范围即可,不需要过程)
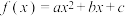 满足下列3个条件:
满足下列3个条件:①
 的图象过坐标原点;②对于任意
的图象过坐标原点;②对于任意 都有
都有 ;③对于任意
;③对于任意 都有
都有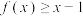 .
.(1)求函数
 的解析式;
的解析式;(2)令
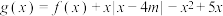 .(其中m为参数)
.(其中m为参数)①求函数
 的单调区间;
的单调区间;②设
 ,函数
,函数 在区间
在区间 上既有最大值又有最小值,请写出实数p,q的取值范围.(用m表示出p,q范围即可,不需要过程)
上既有最大值又有最小值,请写出实数p,q的取值范围.(用m表示出p,q范围即可,不需要过程)
您最近一年使用:0次
2020-01-04更新
|
393次组卷
|
3卷引用:贵州省黔南布依族苗族自治州都匀市民族中学2021-2022学年高一上学期第二次月考数学试题
名校
9 . 已知函数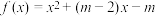 ,
,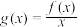 ,且函数
,且函数 是偶函数.
是偶函数.
(1)求 的解析式;
的解析式;
(2)若函数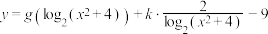 恰好有三个零点,求
恰好有三个零点,求 的值及该函数的零点.
的值及该函数的零点.
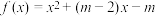 ,
, ,且函数
,且函数 是偶函数.
是偶函数.(1)求
 的解析式;
的解析式;(2)若函数
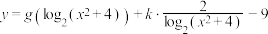 恰好有三个零点,求
恰好有三个零点,求 的值及该函数的零点.
的值及该函数的零点.
您最近一年使用:0次
2019-12-12更新
|
602次组卷
|
2卷引用:贵州省贵阳市2019-2020学年高二上学期联合考试数学(文科)试题
真题
名校
10 . 在 中,内角
中,内角 所对的边分别为a,b,c,已知
所对的边分别为a,b,c,已知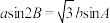 .
.
(Ⅰ)求B;
(Ⅱ)若 ,求sinC的值.
,求sinC的值.
 中,内角
中,内角 所对的边分别为a,b,c,已知
所对的边分别为a,b,c,已知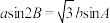 .
.(Ⅰ)求B;
(Ⅱ)若
 ,求sinC的值.
,求sinC的值.
您最近一年使用:0次
2016-12-04更新
|
12584次组卷
|
33卷引用:贵州省贵阳市清镇北大培文学校2018-2019学年高一下学期3月月考数学试题
贵州省贵阳市清镇北大培文学校2018-2019学年高一下学期3月月考数学试题2016年全国普通高等学校招生统一考试文科数学(天津卷精编版)2017届湖南常德一中高三上学期月考二数学(文)试卷2017届河北衡水中学高三上学期一调考试数学(文)试卷2017届河北沧州一中高三10月月考数学(文)试卷西藏自治区拉萨中学2018届高三上学期第二次月考数学(理)试题【全国百强校】内蒙古集宁一中(东校区)2017-2018学年高一下学期期末考试数学(理))试题【全国百强校】四川省凉山木里中学2017-2018学年高一下学期期中考试数学试题【全国百强校】广西南宁市第三中学2018-2019学年高二上学期第一次月考数学试题人教A版 全能练习 正余弦定理 本章基础排查(二)2019年四川省双流中学高三9月月考数学(文)试题陕西省黄陵中学2019-2020学年高二上学期期中考试数学试题新疆生产建设兵团第二中学2019-2020学年高一上学期期末数学试题四川省泸州市泸县第一中学2019-2020学年高一下学期第二次月考数学试题江苏省南通市如东高级中学2019-2020学年高一下学期4月阶段测试数学试题黑龙江省齐齐哈尔市朝鲜族学校2019-2020学年高一下学期期中考试数学试题(已下线)1.1.1正弦定理(1) -2020-2021学年高二数学课时同步练(人教A版必修5)甘肃省会宁县第四中学2019-2020学年高二下学期期末考试数学(文)试题甘肃省会宁县第四中学2019-2020学年高二下学期期末考试数学(理)试题安徽省合肥市第七中学2020-2021学年高三上学期第一次段考文科数学试题(已下线)5.5 三角恒等变换 2020-2021学年高一数学同步课堂帮帮帮(人教A版2019必修第一册)重庆市缙云教育联盟2020-2021学年高一下学期期末数学试题西藏日喀则市南木林高级中学2020-2021学年高二下学期期末测试数学(文)试题甘肃省兰州第一中学2021-2022学年高二上学期期中数学试题重庆市南华中学校2021-2022学年高一下学期第一次调研数学试题(已下线)专题19 解三角形-2023届高考数学一轮复习精讲精练(新高考专用)新疆喀什地区疏勒县实验学校2021-2022学年高一下学期期末考试数学试题福建省福州高级中学2022-2023学年高二上学期9月月考数学试题河南省体育中学2022-2023学年高二上学期期中数学试题广东省广州市第一一三中学2022-2023学年高二上学期阶段二数学试题(已下线)2016年全国普通高等学校招生统一考试文科数学(天津卷参考版)云南省曲靖市宣威市第三中学2023-2024学年高二上学期第四次月考数学试题(已下线)专题20 三角函数及解三角形解答题(文科)-2



