名校
解题方法
1 . “不以规矩,不成方圆”.出自《孟子·离娄章句上》.“规”指圆规,“矩”指由相互垂直的长短两条直尺构成的角尺,用来测量、画圆和方形图案的工具.有一圆形木板,以“矩”量之,较长边为10cm,较短边为5cm,如图所示,将这个圆形木板截出一块三角形木板,三角形定点A,B,C都在圆周上,角A,B,C分别对应a,b,c,满足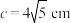 .若
.若 ,且
,且 ,则( )
,则( )

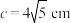 .若
.若 ,且
,且 ,则( )
,则( )
A.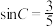 | B.△ABC周长为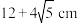 |
C.△ABC周长为 | D.圆形木板的半径为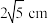 |
您最近一年使用:0次
2023-05-10更新
|
731次组卷
|
5卷引用:湖北省武汉外国语学校2022-2023学年高一下学期期中数学试题
名校
解题方法
2 . 意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数: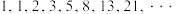 .该数列的特点为前两个数都是1,从第三个数起,每一个数都等于它的前面两个数的和,即
.该数列的特点为前两个数都是1,从第三个数起,每一个数都等于它的前面两个数的和,即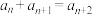 ,人们把这样的一列数组成的数列
,人们把这样的一列数组成的数列 称为“斐波那契数列”,则
称为“斐波那契数列”,则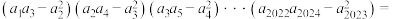 ( ).
( ).
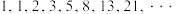 .该数列的特点为前两个数都是1,从第三个数起,每一个数都等于它的前面两个数的和,即
.该数列的特点为前两个数都是1,从第三个数起,每一个数都等于它的前面两个数的和,即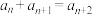 ,人们把这样的一列数组成的数列
,人们把这样的一列数组成的数列 称为“斐波那契数列”,则
称为“斐波那契数列”,则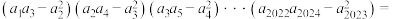 ( ).
( ).| A.-2024 | B.2024 | C.-1 | D.1 |
您最近一年使用:0次
2023-04-28更新
|
874次组卷
|
3卷引用:湖北省十堰市2023届高三下学期四月调研考试数学试题
名校
解题方法
3 . 提丢斯 波得定律是关于太阳系中行星轨道的一个简单的几何学规则,它是在
波得定律是关于太阳系中行星轨道的一个简单的几何学规则,它是在 年由德国的一位中学老师戴维斯
年由德国的一位中学老师戴维斯 提丢斯发现的,后来被柏林天文台的台长波得归纳成一条定律,即数列
提丢斯发现的,后来被柏林天文台的台长波得归纳成一条定律,即数列 :
: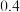 ,
,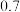 ,
, ,
,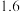 ,
, ,
,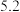 ,
, ,
, 表示的是太阳系第
表示的是太阳系第 颗行星与太阳的平均距离
颗行星与太阳的平均距离 以天文单位
以天文单位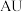 为单位
为单位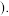 现将数列
现将数列 的各项乘以
的各项乘以 后再减
后再减 ,得到数列
,得到数列 ,可以发现数列
,可以发现数列 从第
从第 项起,每项是前一项的
项起,每项是前一项的 倍,则下列说法正确的是
倍,则下列说法正确的是 ( )
( )
 波得定律是关于太阳系中行星轨道的一个简单的几何学规则,它是在
波得定律是关于太阳系中行星轨道的一个简单的几何学规则,它是在 年由德国的一位中学老师戴维斯
年由德国的一位中学老师戴维斯 提丢斯发现的,后来被柏林天文台的台长波得归纳成一条定律,即数列
提丢斯发现的,后来被柏林天文台的台长波得归纳成一条定律,即数列 :
: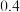 ,
,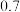 ,
, ,
,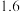 ,
, ,
,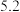 ,
, ,
, 表示的是太阳系第
表示的是太阳系第 颗行星与太阳的平均距离
颗行星与太阳的平均距离 以天文单位
以天文单位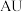 为单位
为单位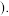 现将数列
现将数列 的各项乘以
的各项乘以 后再减
后再减 ,得到数列
,得到数列 ,可以发现数列
,可以发现数列 从第
从第 项起,每项是前一项的
项起,每项是前一项的 倍,则下列说法正确的是
倍,则下列说法正确的是 ( )
( )A.数列 的通项公式为 的通项公式为 |
B.数列 的第 的第 项为 项为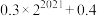 |
C.数列 的前 的前 项和 项和 |
D.数列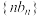 的前 的前 项和 项和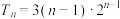 |
您最近一年使用:0次
4 . 我国汉代数学家赵爽为了证明勾股定理,创造了一幅“勾股圆方图”,后人称其为“赵爽弦图”,类比赵爽弦图,用3个全等的小三角形拼成了如图所示的等边 ,若
,若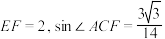 ,则AC=( )
,则AC=( )
 ,若
,若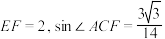 ,则AC=( )
,则AC=( )
| A.8 | B.7 | C.6 | D.5 |
您最近一年使用:0次
2023-04-15更新
|
962次组卷
|
8卷引用:湖北省武汉市5G联合体2022-2023学年高一下学期期中联考数学试题
5 . 明代朱载堉发现的十二平均律,又称“十二等程律”,是世界上通用的一组音(八度)分成十二个半音音程的律制,各相邻两律之间的波长之比完全相同.已知大吕、夹钟、仲吕、林钟、南吕、应钟的波长成等比数列,且大吕和林钟的波长分别是m,n,则夹钟和南吕的波长之积为( )
A.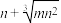 | B.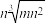 |
C.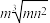 | D.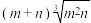 |
您最近一年使用:0次
2023-04-15更新
|
288次组卷
|
4卷引用:湖北省部分学校2022-2023学年高二下学期期中联考数学试题
湖北省部分学校2022-2023学年高二下学期期中联考数学试题辽宁省部分学校联考2022-2023学年高二下学期4月月考数学试题(已下线)4.3.1&4.3.2 等比数列的概念与等比数列的通项公式(8大题型)-【题型分类归纳】2023-2024学年高二数学同步讲与练(苏教版2019选择性必修第一册)(已下线)4.3.1 等比数列的概念(8大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第二册)
名校
解题方法
6 . 赵爽是我国古代数学家,大约在公元222年,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成)类比“赵爽弦图”,可构造如图所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形,设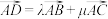 ,若
,若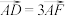 ,则
,则 的值为
的值为______ .
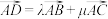 ,若
,若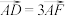 ,则
,则 的值为
的值为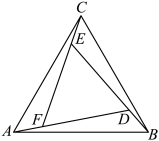
您最近一年使用:0次
2023-04-14更新
|
1351次组卷
|
5卷引用:湖北省孝感市2022-2023学年高一下学期期中联考数学试题
名校
解题方法
7 . 《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九韶的许多创造性成就,其中在卷五“三斜求积”中提出了已知三角形三边 ,
, ,
, ,求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积”若把这段文字写成公式,即
,求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积”若把这段文字写成公式,即 .现有
.现有 满足
满足 .且
.且 的面积为
的面积为 ,请运用上述公式判断下列命题中正确的是( )
,请运用上述公式判断下列命题中正确的是( )
 ,
, ,
, ,求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积”若把这段文字写成公式,即
,求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积”若把这段文字写成公式,即 .现有
.现有 满足
满足 .且
.且 的面积为
的面积为 ,请运用上述公式判断下列命题中正确的是( )
,请运用上述公式判断下列命题中正确的是( )A. 的周长为4 的周长为4 |
B. 的内切圆的面积为 的内切圆的面积为 |
C. 的外接圆半径为 的外接圆半径为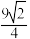 |
D.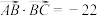 |
您最近一年使用:0次
2023-04-14更新
|
331次组卷
|
3卷引用:湖北省黄冈市黄州中学(黄冈外校)2022-2023学年高一下学期第二次阶段性测试数学试题
湖北省黄冈市黄州中学(黄冈外校)2022-2023学年高一下学期第二次阶段性测试数学试题山西省朔州市怀仁市第一中学2022-2023学年高一下学期期中数学试题(已下线)模块四 专题2 小题进阶提升练(1)(北师大版)
名校
8 . “中国剩余定理”又称“孙子定理”,1852年英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”,“中国剩余定理”讲的是一个关于同余的问题.现有这样一个问题:将正整数中能被3除余1且被2除余1的数按由小到大的顺序排成一列,构成数列 ,则
,则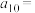 ( )
( )
 ,则
,则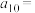 ( )
( )| A.55 | B.49 | C.43 | D.37 |
您最近一年使用:0次
2023-04-13更新
|
2914次组卷
|
9卷引用:湖北省武汉市2023届高三下学期四月调研数学试题
湖北省武汉市2023届高三下学期四月调研数学试题湖北省沙市中学2022-2023学年高二下学期5月月考数学试题(已下线)押新高考第5题 数学新文化专题12数列(选填题)河南省驻马店市驻马店高级中学2022-2023学年高二下学期期中数学试题广东省惠州市龙门县高级中学2024届高三上学期10月月考数学试题(已下线) 第4章 数列单元测试基础卷-2023-2024学年高二数学上学期人教A版(2019)选择性必修第二册广东省肇庆市肇庆中学2023届高三下学期4月月考数学试题四川省成都市成华区某校2023-2024学年高三“三诊”数学(文)试题
名校
9 . 设 为两个正数,定义
为两个正数,定义 的算术平均数为
的算术平均数为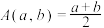 ,几何平均数为
,几何平均数为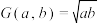 ,则有:
,则有: ,这是我们熟知的基本不等式.上个世纪五十年代,美国数学家D.H.Lehmer提出了“Lehmer均值”,即
,这是我们熟知的基本不等式.上个世纪五十年代,美国数学家D.H.Lehmer提出了“Lehmer均值”,即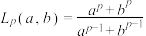 ,其中
,其中 为有理数.下列关系正确的是( )
为有理数.下列关系正确的是( )
 为两个正数,定义
为两个正数,定义 的算术平均数为
的算术平均数为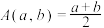 ,几何平均数为
,几何平均数为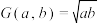 ,则有:
,则有: ,这是我们熟知的基本不等式.上个世纪五十年代,美国数学家D.H.Lehmer提出了“Lehmer均值”,即
,这是我们熟知的基本不等式.上个世纪五十年代,美国数学家D.H.Lehmer提出了“Lehmer均值”,即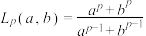 ,其中
,其中 为有理数.下列关系正确的是( )
为有理数.下列关系正确的是( )A.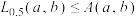 | B.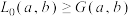 |
C.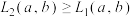 | D.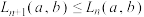 |
您最近一年使用:0次
2023-04-11更新
|
1480次组卷
|
4卷引用:湖北省孝感高级中学2023-2024学年高一上学期9月调研考试数学试题
10 . 数学家杨辉在其专著《详解九章算术法》和《算法通变本末》中,提出了一些新的高阶等差数列,其中二阶等差数列是一个常见的高阶等差数列,如数列2,4,7,11,16,从第二项起,每一项与前一项的差组成新数列2,3,4,5,新数列2,3,4,5为等差数列,则称数列2,4,7,11,16为二阶等差数列.现有二阶等差数列 ,其中前几项分别为2,5,9,14,20,27,记该数列的后一项与前一项之差组成新数列
,其中前几项分别为2,5,9,14,20,27,记该数列的后一项与前一项之差组成新数列 ,则
,则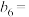 ( )
( )
 ,其中前几项分别为2,5,9,14,20,27,记该数列的后一项与前一项之差组成新数列
,其中前几项分别为2,5,9,14,20,27,记该数列的后一项与前一项之差组成新数列 ,则
,则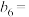 ( )
( )| A.5 | B.6 | C.7 | D.8 |
您最近一年使用:0次



