解题方法
1 . 已知幂的基本不等式:当 ,
, 时,
时, .请利用此基本不等式解决下列相关问题:
.请利用此基本不等式解决下列相关问题:
(1)当 ,
, 时,求
时,求 的取值范围;
的取值范围;
(2)当 ,
, 时,求证:
时,求证: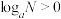 ;
;
(3)利用(2)证明对数函数的单调性:当 时,对数函数
时,对数函数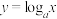 在
在 上是严格增函数.
上是严格增函数.
 ,
, 时,
时, .请利用此基本不等式解决下列相关问题:
.请利用此基本不等式解决下列相关问题:(1)当
 ,
, 时,求
时,求 的取值范围;
的取值范围;(2)当
 ,
, 时,求证:
时,求证: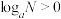 ;
;(3)利用(2)证明对数函数的单调性:当
 时,对数函数
时,对数函数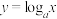 在
在 上是严格增函数.
上是严格增函数.
您最近一年使用:0次
2 . 如果函数 满足:对于任意
满足:对于任意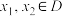 ,均有
,均有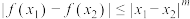 (m为正整数)成立,则称函数在D上具有“m级”性质.
(m为正整数)成立,则称函数在D上具有“m级”性质.
(1)分别判断函数 ,
, ,是否在R上具有“1级”性质,并说明理由;
,是否在R上具有“1级”性质,并说明理由;
(2)设函数 在R具有“m级”性质,对任意的实数a,证明函数
在R具有“m级”性质,对任意的实数a,证明函数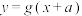 具有“m级”性质;
具有“m级”性质;
(3)若函数 在区间
在区间 以及区间
以及区间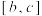 (
(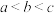 )上都具有“1级”性质,求证:该函数在区间
)上都具有“1级”性质,求证:该函数在区间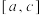 上具有“1级”性质.
上具有“1级”性质.
 满足:对于任意
满足:对于任意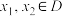 ,均有
,均有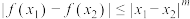 (m为正整数)成立,则称函数在D上具有“m级”性质.
(m为正整数)成立,则称函数在D上具有“m级”性质.(1)分别判断函数
 ,
, ,是否在R上具有“1级”性质,并说明理由;
,是否在R上具有“1级”性质,并说明理由;(2)设函数
 在R具有“m级”性质,对任意的实数a,证明函数
在R具有“m级”性质,对任意的实数a,证明函数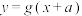 具有“m级”性质;
具有“m级”性质;(3)若函数
 在区间
在区间 以及区间
以及区间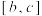 (
(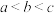 )上都具有“1级”性质,求证:该函数在区间
)上都具有“1级”性质,求证:该函数在区间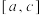 上具有“1级”性质.
上具有“1级”性质.
您最近一年使用:0次
名校
3 . 若函数 的定义域为
的定义域为 ,且对于任意的
,且对于任意的 、
、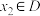 ,“
,“ ”的充要条件是“
”的充要条件是“ ”,则称函数
”,则称函数 为
为 上的“单值函数”.对于函数
上的“单值函数”.对于函数 ,记
,记
 ,
,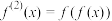 ,
,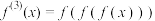 ,…,
,…,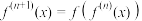 ,其中
,其中 ,2,3,…,并对任意的
,2,3,…,并对任意的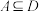 ,记集合
,记集合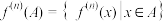 ,并规定
,并规定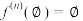 .
.
(1)若 ,函数
,函数 的定义域为
的定义域为 ,求
,求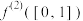 和
和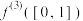 ;
;
(2)若函数 的定义域为
的定义域为 ,且存在正整数
,且存在正整数 ,使得对任意的
,使得对任意的 ,
,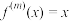 ,求证:函数
,求证:函数 为
为 上的“单值函数”;
上的“单值函数”;
(3)设 ,若函数
,若函数 的定义域为
的定义域为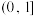 ,且表达式为:
,且表达式为: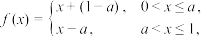
判断 是否为
是否为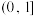 上的“单值函数”,并证明对任意的区间
上的“单值函数”,并证明对任意的区间 ,存在正整数
,存在正整数 ,使得
,使得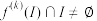 .
.
 的定义域为
的定义域为 ,且对于任意的
,且对于任意的 、
、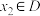 ,“
,“ ”的充要条件是“
”的充要条件是“ ”,则称函数
”,则称函数 为
为 上的“单值函数”.对于函数
上的“单值函数”.对于函数 ,记
,记 ,
,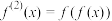 ,
,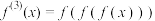 ,…,
,…,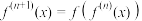 ,其中
,其中 ,2,3,…,并对任意的
,2,3,…,并对任意的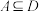 ,记集合
,记集合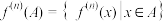 ,并规定
,并规定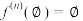 .
.(1)若
 ,函数
,函数 的定义域为
的定义域为 ,求
,求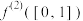 和
和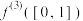 ;
;(2)若函数
 的定义域为
的定义域为 ,且存在正整数
,且存在正整数 ,使得对任意的
,使得对任意的 ,
,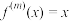 ,求证:函数
,求证:函数 为
为 上的“单值函数”;
上的“单值函数”;(3)设
 ,若函数
,若函数 的定义域为
的定义域为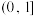 ,且表达式为:
,且表达式为: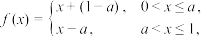
判断
 是否为
是否为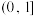 上的“单值函数”,并证明对任意的区间
上的“单值函数”,并证明对任意的区间 ,存在正整数
,存在正整数 ,使得
,使得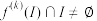 .
.
您最近一年使用:0次
名校
解题方法
4 . 已知函数 与
与 的定义域为R,若对任意区间
的定义域为R,若对任意区间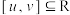 ,存在
,存在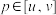 且
且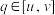 ,使
,使 ,则
,则 是
是 的生成函数.
的生成函数.
(1)求证: 是
是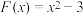 的生成函数;
的生成函数;
(2)若 是
是 的生成函数,判断并证明
的生成函数,判断并证明 的单调性;
的单调性;
(3)若 是
是 的生成函数,实数
的生成函数,实数 ,求
,求 的一个生成函数.
的一个生成函数.
 与
与 的定义域为R,若对任意区间
的定义域为R,若对任意区间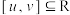 ,存在
,存在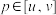 且
且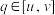 ,使
,使 ,则
,则 是
是 的生成函数.
的生成函数.(1)求证:
 是
是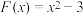 的生成函数;
的生成函数;(2)若
 是
是 的生成函数,判断并证明
的生成函数,判断并证明 的单调性;
的单调性;(3)若
 是
是 的生成函数,实数
的生成函数,实数 ,求
,求 的一个生成函数.
的一个生成函数.
您最近一年使用:0次
2023-05-05更新
|
570次组卷
|
4卷引用:上海交通大学附属中学2022-2023学年高一下学期期中数学试题
上海交通大学附属中学2022-2023学年高一下学期期中数学试题(已下线)5.2.2 函数的单调性-数学同步精品课堂(沪教版2020必修第一册)湖南省长沙市明德中学2022-2023学年高一下学期5月月考数学试题(已下线)第3课时 课后 函数的单调性(完成)
5 . 证明:
(1)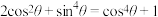 .
.
(2)已知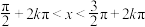 ,
,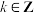 ,求证:
,求证: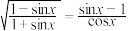
(1)
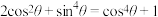 .
.(2)已知
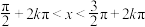 ,
,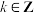 ,求证:
,求证: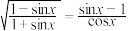
您最近一年使用:0次
名校
6 . 给定不共面的4点,作过其中3个点的平面,所有4个这样的平面围成的几何体称为四面体(如图所示),预先给定的4个点称为四面体的顶点,2个顶点的连线称为四面体的棱,3个顶点所确定的三角形称为四面体的面.求证:四面体中任何一对不共顶点的棱所在的直线一定是异面直线.
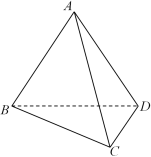
(1)请你用异面直线判定定理证明该结论;
(2)请你用反证法证明该结论.

(1)请你用异面直线判定定理证明该结论;
(2)请你用反证法证明该结论.
您最近一年使用:0次
7 . 已知函数 的定义域为
的定义域为 ,
, 为大于
为大于 的常数,对任意
的常数,对任意 ,都满足
,都满足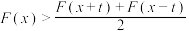 ,则称函数
,则称函数 在
在 上具有“性质
上具有“性质 ”.
”.
(1)试判断函数 和函数
和函数 是否具有“性质
是否具有“性质 ”(无需证明);
”(无需证明);
(2)若函数 具有“性质
具有“性质 ”,且
”,且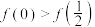 ,求证:对任意
,求证:对任意 ,都有
,都有 ;
;
(3)若函数 的定义域为
的定义域为 ,且具有“性质
,且具有“性质 ”,试判断下列命题的真假,并说明理由,
”,试判断下列命题的真假,并说明理由,
①若 在区间
在区间 上是严格增函数,则此函数在
上是严格增函数,则此函数在 上也是严格增函数;
上也是严格增函数;
②若 在区间
在区间 上是严格减函数,则此函数在
上是严格减函数,则此函数在 上也是严格减函数.
上也是严格减函数.
 的定义域为
的定义域为 ,
, 为大于
为大于 的常数,对任意
的常数,对任意 ,都满足
,都满足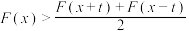 ,则称函数
,则称函数 在
在 上具有“性质
上具有“性质 ”.
”.(1)试判断函数
 和函数
和函数 是否具有“性质
是否具有“性质 ”(无需证明);
”(无需证明);(2)若函数
 具有“性质
具有“性质 ”,且
”,且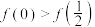 ,求证:对任意
,求证:对任意 ,都有
,都有 ;
;(3)若函数
 的定义域为
的定义域为 ,且具有“性质
,且具有“性质 ”,试判断下列命题的真假,并说明理由,
”,试判断下列命题的真假,并说明理由,①若
 在区间
在区间 上是严格增函数,则此函数在
上是严格增函数,则此函数在 上也是严格增函数;
上也是严格增函数;②若
 在区间
在区间 上是严格减函数,则此函数在
上是严格减函数,则此函数在 上也是严格减函数.
上也是严格减函数.
您最近一年使用:0次
2023-01-12更新
|
629次组卷
|
6卷引用:上海市闵行区2022-2023学年高一上学期期末数学试题
上海市闵行区2022-2023学年高一上学期期末数学试题(已下线)第五章 函数的概念、性质及应用(压轴必刷30题9种题型专项训练)-【满分全攻略】(沪教版2020必修第一册)(已下线)专题10 指数及指数函数压轴题-【常考压轴题】(已下线)期末真题必刷压轴60题(10个考点专练)-【满分全攻略】(沪教版2020必修第一册)(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】(人教A版2019必修第一册)(已下线)第四章 指数函数与对数函数-【优化数学】单元测试能力卷(人教A版2019)
名校
8 . (1)求证:已知 ,
, ,
, ,
,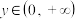 ,
,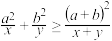 ,并指出等号成立的条件;
,并指出等号成立的条件;
(2)求证:对任意的 ,关于
,关于 的两个方程
的两个方程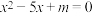 与
与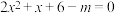 至少有一个方程有实数根(反证法证明);
至少有一个方程有实数根(反证法证明);
(3)求证:使得不等式 对一切实数
对一切实数 ,
, ,
, 都成立的充要条件是
都成立的充要条件是 ,
, ,
, 且
且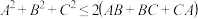 .
.
 ,
, ,
, ,
,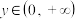 ,
,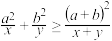 ,并指出等号成立的条件;
,并指出等号成立的条件;(2)求证:对任意的
 ,关于
,关于 的两个方程
的两个方程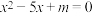 与
与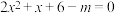 至少有一个方程有实数根(反证法证明);
至少有一个方程有实数根(反证法证明);(3)求证:使得不等式
 对一切实数
对一切实数 ,
, ,
, 都成立的充要条件是
都成立的充要条件是 ,
, ,
, 且
且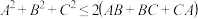 .
.
您最近一年使用:0次
名校
9 . 定理(三角不等式),对于任意的 、
、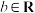 ,恒有
,恒有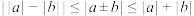 .定义:已知
.定义:已知 且
且 ,对于有序数组
,对于有序数组 、
、 、
、 、
、 ,称
,称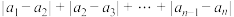 为有序数组
为有序数组 、
、 、
、 、
、 的波动距离,记作
的波动距离,记作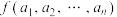 ,即
,即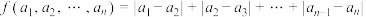 ,请根据上述俼息解决以下几个问题:
,请根据上述俼息解决以下几个问题:
(1)求函数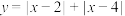 的最小值,并指出函数取到最小值时
的最小值,并指出函数取到最小值时 的取值范围;
的取值范围;
(2)①求有序数组 、
、 、
、 、
、 的波动距离
的波动距离 ;
;
②求证:若 、
、 、
、 、
、 且
且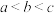 ,则
,则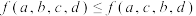 ;题(注:该命题无需证明,需要时可直接使用).设两两不相等的四个实数
;题(注:该命题无需证明,需要时可直接使用).设两两不相等的四个实数 、
、 、
、 、
、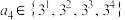 ,求有序数组
,求有序数组 、
、 、
、 、
、 的波动距离
的波动距离 的最大值.
的最大值.
 、
、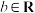 ,恒有
,恒有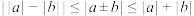 .定义:已知
.定义:已知 且
且 ,对于有序数组
,对于有序数组 、
、 、
、 、
、 ,称
,称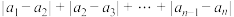 为有序数组
为有序数组 、
、 、
、 、
、 的波动距离,记作
的波动距离,记作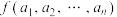 ,即
,即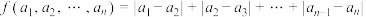 ,请根据上述俼息解决以下几个问题:
,请根据上述俼息解决以下几个问题:(1)求函数
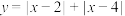 的最小值,并指出函数取到最小值时
的最小值,并指出函数取到最小值时 的取值范围;
的取值范围;(2)①求有序数组
 、
、 、
、 、
、 的波动距离
的波动距离 ;
;②求证:若
 、
、 、
、 、
、 且
且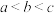 ,则
,则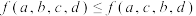 ;题(注:该命题无需证明,需要时可直接使用).设两两不相等的四个实数
;题(注:该命题无需证明,需要时可直接使用).设两两不相等的四个实数 、
、 、
、 、
、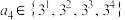 ,求有序数组
,求有序数组 、
、 、
、 、
、 的波动距离
的波动距离 的最大值.
的最大值.
您最近一年使用:0次
2022-08-22更新
|
416次组卷
|
7卷引用:上海市控江中学2021-2022学年高一上学期期中数学试题
上海市控江中学2021-2022学年高一上学期期中数学试题上海市高桥中学2022-2023学年高一上学期期中数学试题(已下线)期中模拟预测卷03(测试范围:前三章)-2022-2023学年高一数学上学期期中期末考点大串讲(沪教版2020必修第一册)(已下线)上海高一上学期期中【压轴42题专练】(2)(已下线)第二章 等式与不等式(压轴题专练)-速记·巧练(沪教版2020必修第一册)上海市吴淞中学2023-2024学年高一上学期期中数学试题(已下线)专题02 等式与不等式(练习)-2
名校
10 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.
例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵ ,∴
,∴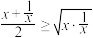 ,即
,即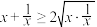 ,∴
,∴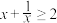 ,
,
当且仅当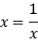 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)已知如 ,求下列各式的值:
,求下列各式的值:
①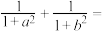 ___________.
___________.
②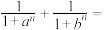 ___________.
___________.
(2)若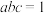 ,解方程
,解方程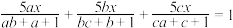 .
.
(3)若正数a、b满足 ,求
,求 的最小值.
的最小值.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如,
 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式
 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.例如:在
 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵
 ,∴
,∴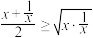 ,即
,即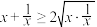 ,∴
,∴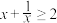 ,
,当且仅当
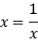 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题
(1)已知如
 ,求下列各式的值:
,求下列各式的值:①
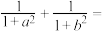 ___________.
___________.②
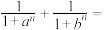 ___________.
___________.(2)若
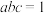 ,解方程
,解方程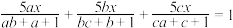 .
.(3)若正数a、b满足
 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2021-10-29更新
|
530次组卷
|
3卷引用:第二章 等式与不等式(压轴题专练)-速记·巧练(沪教版2020必修第一册)
(已下线)第二章 等式与不等式(压轴题专练)-速记·巧练(沪教版2020必修第一册)江苏省南通中学2020-2021学年高一上学期开学考试数学试题江西省南昌市第二中学2023-2024学年高一上学期月考数学试题(一)



