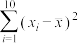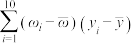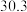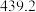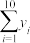解题方法
1 . 若函数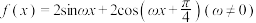 的一个周期是
的一个周期是 ,则
,则 的取值可以是
的取值可以是___________ .(写出一个即可).
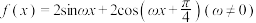 的一个周期是
的一个周期是 ,则
,则 的取值可以是
的取值可以是
您最近一年使用:0次
2022-01-30更新
|
494次组卷
|
2卷引用:广西南宁市2022-2023学年高一上学期期末数学模拟试题
2 . 某高中三年级的甲、乙两个同学同时参加某大学的自主招生,在申请的材料中提交了某学科10次的考试成绩,记录如下:
甲:78 86 95 97 88 82 76 89 92 95
乙:73 83 69 82 93 86 79 75 84 99
(1)根据两组数据,作出两人成绩的茎叶图,并通过茎叶图比较两人本学科成绩平均值的大小关系及方差的大小关系(不要求计算具体值,直接写出结论即可)
(2)现将两人的名次分为三个等级:
根据所给数据,从甲、乙获得“优秀”的成绩组合中随机选取一组,求选中甲同学成绩高于乙同学成绩的组合的概率.
甲:78 86 95 97 88 82 76 89 92 95
乙:73 83 69 82 93 86 79 75 84 99
(1)根据两组数据,作出两人成绩的茎叶图,并通过茎叶图比较两人本学科成绩平均值的大小关系及方差的大小关系(不要求计算具体值,直接写出结论即可)
(2)现将两人的名次分为三个等级:
| 成绩分数 | 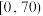 | 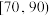 | 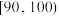 |
| 等级 | 合格 | 良好 | 优秀 |
您最近一年使用:0次
2019-02-05更新
|
515次组卷
|
3卷引用:【市级联考】广西钦州市2018-2019学年高二上学期期末考试数学(理)试题
名校
3 . 手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
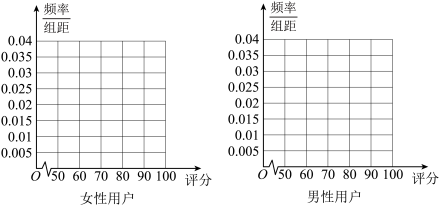
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);
(2)把评分不低于70分的用户称为“评分良好用户”,完成下列列联表,并判断能否有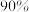 的把握认为“评分良好用户”与性别有关?
的把握认为“评分良好用户”与性别有关?
参考附表:
参考公式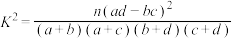 ,其中
,其中

| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
(2)把评分不低于70分的用户称为“评分良好用户”,完成下列列联表,并判断能否有
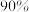 的把握认为“评分良好用户”与性别有关?
的把握认为“评分良好用户”与性别有关?| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | |||
| “不认可”手机 | |||
| 合计 |
 |  | 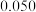 |  |  |
 |  |  |  |  |
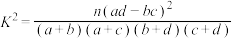 ,其中
,其中
您最近一年使用:0次
2019-05-28更新
|
472次组卷
|
4卷引用:广西壮族自治区南宁市2018-2019学年高二下学期期末数学试题
广西壮族自治区南宁市2018-2019学年高二下学期期末数学试题广西南宁市2018-2019学年高二下学期“4+ N”高中联合体期末数学(理)试题【全国百强校】北京市清华大学附属中学2019届高三下学期第三次模拟考试数学(文)试题(已下线)专题10 概率与统计——2019年高考真题和模拟题文科数学分项汇编
名校
解题方法
4 . 《中共中央国务院关于全面推进乡村振兴加快农业农村现代化的意见》,这是21世纪以来第 个指导“三农”工作的中央一号文件.文件指出,民族要复兴,乡村必振兴,要大力推进数字乡村建设,推进智慧农业发展.某乡村合作社借助互联网直播平台进行农产品销售,众多网红主播参与到直播当中,在众多网红直播中,统计了
个指导“三农”工作的中央一号文件.文件指出,民族要复兴,乡村必振兴,要大力推进数字乡村建设,推进智慧农业发展.某乡村合作社借助互联网直播平台进行农产品销售,众多网红主播参与到直播当中,在众多网红直播中,统计了 名网红直播的观看人次
名网红直播的观看人次 和农产品销售量
和农产品销售量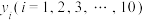 的数据,得到如图所示的散点图.
的数据,得到如图所示的散点图.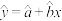 和
和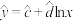 哪一个更适合作为观看人次
哪一个更适合作为观看人次 和销售量
和销售量 的回归方程类型;(只要给出判断即可,不必说明理由)
的回归方程类型;(只要给出判断即可,不必说明理由)
(2)对数据作出如下处理:得到相关统计量的值如表:
其中令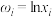 ,
, .
.
根据(1)的判断结果及表中数据,求 (单位:千件)关于
(单位:千件)关于 (单位:十万次)的回归方程,并预测当观看人次为
(单位:十万次)的回归方程,并预测当观看人次为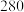 万人时的销售量;
万人时的销售量;
参考数据和公式: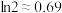 ,
,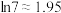
附:对于一组数据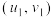 、
、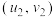 、
、 、
、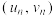 ,其回归线
,其回归线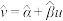 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: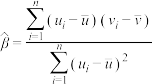 ,
, .
.
 个指导“三农”工作的中央一号文件.文件指出,民族要复兴,乡村必振兴,要大力推进数字乡村建设,推进智慧农业发展.某乡村合作社借助互联网直播平台进行农产品销售,众多网红主播参与到直播当中,在众多网红直播中,统计了
个指导“三农”工作的中央一号文件.文件指出,民族要复兴,乡村必振兴,要大力推进数字乡村建设,推进智慧农业发展.某乡村合作社借助互联网直播平台进行农产品销售,众多网红主播参与到直播当中,在众多网红直播中,统计了 名网红直播的观看人次
名网红直播的观看人次 和农产品销售量
和农产品销售量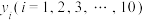 的数据,得到如图所示的散点图.
的数据,得到如图所示的散点图.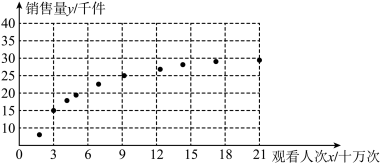
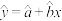 和
和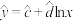 哪一个更适合作为观看人次
哪一个更适合作为观看人次 和销售量
和销售量 的回归方程类型;(只要给出判断即可,不必说明理由)
的回归方程类型;(只要给出判断即可,不必说明理由)(2)对数据作出如下处理:得到相关统计量的值如表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
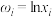 ,
, .
.根据(1)的判断结果及表中数据,求
 (单位:千件)关于
(单位:千件)关于 (单位:十万次)的回归方程,并预测当观看人次为
(单位:十万次)的回归方程,并预测当观看人次为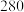 万人时的销售量;
万人时的销售量;参考数据和公式:
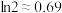 ,
,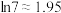
附:对于一组数据
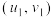 、
、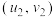 、
、 、
、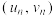 ,其回归线
,其回归线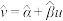 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: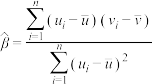 ,
, .
.
您最近一年使用:0次
2023-04-16更新
|
1021次组卷
|
6卷引用:广西百色市2022-2023学年高二下学期期末教学质量调研数学试题
广西百色市2022-2023学年高二下学期期末教学质量调研数学试题吉林省长春市十一高中2022-2023学年高二下学期第一学程考试数学试题 福建省政和县第一中学2022-2023学年高二下学期期中测试数学试题(已下线)模块三 专题1 大题分类练(线性回归)(北师大高二)(已下线)第八章:成对数据的统计分析章末重点题型复习(10题型)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)高二下学期期末复习解答题压轴题二十二大题型专练(5)
名校
解题方法
5 . 2020年,是人类首次成功从北坡登顶珠峰60周年,也是中国首次精确测定并公布珠峰高程的45周年.华为帮助中国移动开通珠峰峰顶5G,有助于测量信号的实时开通,为珠峰高程测量提供通信保障,也验证了超高海拔地区5G信号覆盖的可能性,在持续高风速下5G信号的稳定性,在条件恶劣地区通过简易设备传输视频信号的可能性.正如任总在一次采访中所说:“华为公司价值体系的理想是为人类服务.”有人曾问,在珠峰开通5G的意义在哪里?“我认为它是科学技术的一次珠峰登顶,告诉全世界,华为5G、中国5G的底气来自哪里.现在,5G的到来给人们的生活带来更加颠覆性的变革,某IT公司基于领先技术的支持,5G经济收入在短期内逐月攀升,该IT公司在1月份至6月份的5G经济收入y(单位:百万元)关于月份x的数据如下表所示,并根据数据绘制了如图所示的散点图.
(1)根据散点图判断,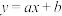 与
与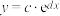 (a,b,c,d均为常数)哪一个更适宜作为5G经济收入y关于月份x的回归方程类型?(给出判断即可,不必说明理由)
(a,b,c,d均为常数)哪一个更适宜作为5G经济收入y关于月份x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的结果及表中的数据,求出y关于x的回归方程,并预测该公司7月份的5G经济收入.(结果保留小数点后两位)
(3)从前6个月的收入中抽取2个,记收入超过20百万元的个数为X,求X的分布列和数学期望.参考数据:
其中,设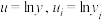 (i=1,2,3,4,5,6).
(i=1,2,3,4,5,6).
参考公式:对于一组具有线性相关关系的数据( ,
,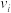 )(i=1,2,3,…,n),其回归直线
)(i=1,2,3,…,n),其回归直线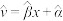 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为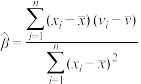 ,
, .
.
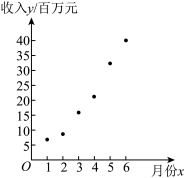
月份x | 1 | 2 | 3 | 4 | 5 | 6 |
收入y(百万元) | 6.6 | 8.6 | 16.1 | 21.6 | 33.0 | 41.0 |
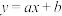 与
与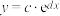 (a,b,c,d均为常数)哪一个更适宜作为5G经济收入y关于月份x的回归方程类型?(给出判断即可,不必说明理由)
(a,b,c,d均为常数)哪一个更适宜作为5G经济收入y关于月份x的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的结果及表中的数据,求出y关于x的回归方程,并预测该公司7月份的5G经济收入.(结果保留小数点后两位)
(3)从前6个月的收入中抽取2个,记收入超过20百万元的个数为X,求X的分布列和数学期望.参考数据:
 | 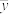 | 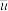 |  |  | 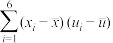 | 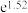 |  |
| 3.50 | 21.15 | 2.85 | 17.70 | 125.35 | 6.73 | 4.57 | 14.30 |
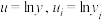 (i=1,2,3,4,5,6).
(i=1,2,3,4,5,6).参考公式:对于一组具有线性相关关系的数据(
 ,
,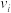 )(i=1,2,3,…,n),其回归直线
)(i=1,2,3,…,n),其回归直线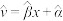 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为 ,
, .
.
您最近一年使用:0次
2023-01-22更新
|
2413次组卷
|
15卷引用:广西南宁市第二中学2023届高三上学期1月月考(期末)数学(理)试题
广西南宁市第二中学2023届高三上学期1月月考(期末)数学(理)试题广西柳州市第三中学2023届高三下学期2月开学考数学(理)试题四川省成都石室中学2021-2022学年高三下学期“二诊模拟”文科数学试题四川省成都石室中学2021-2022学年高三下学期“二诊模拟”理科数学试题河北省张家口市第一中学2022届高三下学期4月月考数学试题(已下线)必刷卷01-2022年高考数学考前信息必刷卷(新高考地区专用)湖南省株洲市第二中学2023届高三下学期第一次月考数学试题(已下线)第八章 成对数据的统计分析(A卷·知识通关练)-【单元测试】2022-2023学年高二数学分层训练AB卷(人教A版2019)(已下线)拓展一:数学建模 建立统计模型进行预测(非线性回归模型) (综合)-【精讲精练】2022-2023学年高二数学下学期同步精讲精练(人教A版2019选择性必修第三册)辽宁省六校协作体2022-2023学年高二下学期3月联考数学试题辽宁省鞍山市2023届高三第二次质量监测数学试题(已下线)专题10 计数原理与概率统计(理科)(已下线)专题15 押全国卷第19题 统计与概率(已下线)8.1成对数据的相关分析(分层练习)-2022-2023学年高二数学同步精品课堂(沪教版2020选择性必修第二册)(已下线)专题16 统计
6 . 为检测空气质量,某市环保局随机抽取了甲、乙两地2016年20天的PM2.5日平均浓度(单位:微克/立方米)是监测数据,得到甲地PM2.5日平均浓度的频率分布直方图和乙地PM2.5日平均浓度的频数分布表.
(1)根据乙地20天PM2.5日平均浓度的频数分布表作出相应的频率分布直方图,并通过两个频率分布直方图比较两地PM2.5日平均浓度的平均值及分散程度;(不要求计算出具体值,给出结论即可)
(2)求甲地20天PM2.5日平均浓度的中位数;
(3)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:

记事件 :“甲地市民对空气质量的满意度等级为不满意”.根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件
:“甲地市民对空气质量的满意度等级为不满意”.根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件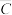 的概率.
的概率.
甲地20天PM2.5日平均浓度频率分布直方图

乙地20天PM2.5日平均浓度频数分布表

(1)根据乙地20天PM2.5日平均浓度的频数分布表作出相应的频率分布直方图,并通过两个频率分布直方图比较两地PM2.5日平均浓度的平均值及分散程度;(不要求计算出具体值,给出结论即可)
(2)求甲地20天PM2.5日平均浓度的中位数;
(3)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:

记事件
 :“甲地市民对空气质量的满意度等级为不满意”.根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件
:“甲地市民对空气质量的满意度等级为不满意”.根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件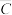 的概率.
的概率.
您最近一年使用:0次
真题
名校
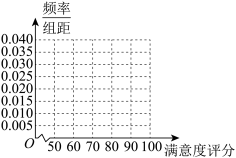
7 . 某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.
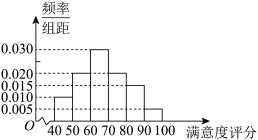
A地区用户满意度评分的频率分布直方图
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.(不要求计算出具体值,给出结论即可)
B地区用户满意度评分的频率分布直方图
估计哪个地区的用户的满意度等级为不满意的概率大,说明理由.
A地区用户满意度评分的频率分布直方图
| 满意度评分分组 | 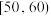 | 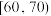 | 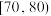 | 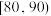 | 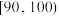 |
| 频数 | 2 | 8 | 14 | 10 | 6 |
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.(不要求计算出具体值,给出结论即可)
B地区用户满意度评分的频率分布直方图
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的用户的满意度等级为不满意的概率大,说明理由.
您最近一年使用:0次
2016-12-03更新
|
9731次组卷
|
19卷引用:广西南宁市马山县金伦中学2016-2017学年高二下学期期末考试数学(文)试题
广西南宁市马山县金伦中学2016-2017学年高二下学期期末考试数学(文)试题2015年全国普通高等学校招生统一考试文科数学(新课标Ⅱ)内蒙古巴彦淖尔市第一中学2017-2018学年高二12月月考数学试题人教B版高中数学必修三同步测试:模块综合测评1人教B版(2019) 必修第二册 过关斩将 第五章 5.1 统计 5.1.4 用样本估计总体(已下线)专题10.2 用样本估计总体(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题31 概率和统计【文】-十年(2011-2020)高考真题数学分项(已下线)测试卷26 统计(B)-2021届高考数学一轮复习(文理通用)单元过关测试卷(已下线)专题10.2 用样本估计总体 (精讲) -2021年高考数学(理)一轮复习讲练测(已下线)5.1.4 用样本估计总体-2020-2021学年高一数学课时同步练(人教B版2019必修第二册)(已下线)专题14 概率统计-十年(2012-2021)高考数学真题分项汇编(全国通用)湖北省黄石市大冶市第一中学2021-2022学年高二上学期9月月考数学试题(已下线)考点68 统计初步-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】沪教版(2020) 必修第三册 精准辅导 第13章 13.5(1) 估计总体分布江苏省无锡市第一中学2021-2022学年高一下学期5月月考数学试题(已下线)专题14 概率统计解答题-2新疆维吾尔自治区乌鲁木齐市第四中学2024届高三上学期12月月考数学试题(已下线)9.1 随机抽样与统计图标(高考真题素材之十年高考)(已下线)专题25 概率统计解答题(文科)
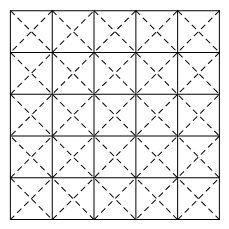
8 . 发现问题是数学建模的第一步,对我们中学生来说养成发现问题并将问题记录下来的习惯相当重要.相传2500多年前,古希腊数学家毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面的图案(如图)反映了直角三角形三边的某种数量关系,他将自己的发现记录下来,经过后续研究发现了勾股定理.请你也来仔细观察,观察图中的多边形面积,然后用文字写出你的一个关于多边形面积的发现:________ (提示:答案可以是疑问句,也可以陈述句,答案不唯一).

您最近一年使用:0次
2022-07-09更新
|
1336次组卷
|
6卷引用:广西钦州市2021-2022学年高一下学期教学质量监测(期末)数学试题
广西钦州市2021-2022学年高一下学期教学质量监测(期末)数学试题(已下线)专题24 毕达哥拉斯(已下线)【高中数学数学文化鉴赏与学习】 专题24 毕达哥拉斯(以毕达哥拉斯(定理)为背景的高中数学考题题组训练)(已下线)技巧03 数学文化与数学阅读解题策略(精讲精练)-2(已下线)专题3 “数学建模”类型云南省昆明市官渡区艺卓中学2023届高三下学期第二次月考数学试题
解题方法
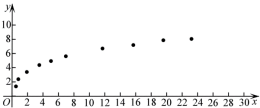
9 . 今年全国两会期间,习近平总书记在看望参加全国政协十三届五次会议的农业界、社会福利和社会保障界委员时指出“粮食安全是‘国之大者’.悠悠万事,吃饭为大.”某校课题小组针对粮食产量与化肥施用量间关系进行研究,收集了10组化肥施用量和粮食亩产量的数据,并对这些数据作了初步处理,得到了如图所示的散点图及一些统计量的值.每亩化肥施用量为x(单位:公斤),粮食亩产量为y(单位:百公斤).
参考数据:
表中 ,
,
(1)根据散点图判断, 与
与 ,哪一个适宜作为粮食亩产量y关于每亩化肥施用量x的回归方程(给出判断即可,不必说明理由);
,哪一个适宜作为粮食亩产量y关于每亩化肥施用量x的回归方程(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;并预测每亩化肥施用量为27公斤时,粮食亩产量y的值;
附:①对于一组数据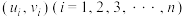 ,其回归直线
,其回归直线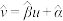 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ;②取
;②取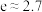 .
.

参考数据:
|
|
|
|
|
|
|
|
650 | 91.5 | 52.5 | 1478.6 | 30.5 | 15 | 15 | 46.5 |
 ,
,
(1)根据散点图判断,
 与
与 ,哪一个适宜作为粮食亩产量y关于每亩化肥施用量x的回归方程(给出判断即可,不必说明理由);
,哪一个适宜作为粮食亩产量y关于每亩化肥施用量x的回归方程(给出判断即可,不必说明理由);(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;并预测每亩化肥施用量为27公斤时,粮食亩产量y的值;
附:①对于一组数据
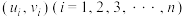 ,其回归直线
,其回归直线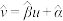 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ;②取
;②取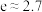 .
.
您最近一年使用:0次
2022-05-10更新
|
415次组卷
|
2卷引用:广西百色市2021-2022学年高二下学期期末教学质量调研测试数学(文)试题
解题方法
10 . 已知二次函数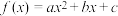 (其中
(其中 )满足下列三个条件:①
)满足下列三个条件:① 图象过坐标原点;②对于任意
图象过坐标原点;②对于任意 都
都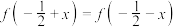 成立;③方程
成立;③方程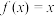 有两个相等的实数根.
有两个相等的实数根.
(1)求函数 的解析式;
的解析式;
(2)令 (其中
(其中 ),求函数
),求函数 的单调区间(直接写出结果即可);
的单调区间(直接写出结果即可);
(3)研究方程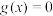 在区间
在区间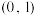 内的解的个数.
内的解的个数.
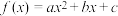 (其中
(其中 )满足下列三个条件:①
)满足下列三个条件:① 图象过坐标原点;②对于任意
图象过坐标原点;②对于任意 都
都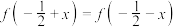 成立;③方程
成立;③方程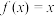 有两个相等的实数根.
有两个相等的实数根.(1)求函数
 的解析式;
的解析式;(2)令
 (其中
(其中 ),求函数
),求函数 的单调区间(直接写出结果即可);
的单调区间(直接写出结果即可);(3)研究方程
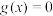 在区间
在区间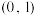 内的解的个数.
内的解的个数.
您最近一年使用:0次