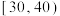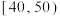解题方法
1 . 将数列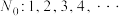 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列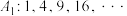 ,此时数列
,此时数列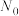 中剩下的项构成数列
中剩下的项构成数列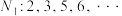 ;再将数列
;再将数列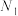 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列 ,剩下的项构成数列
,剩下的项构成数列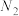 ;….如此操作下去,将数列
;….如此操作下去,将数列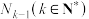 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列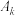 ,剩下的项构成数列
,剩下的项构成数列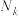 .
.
(1)分别写出数列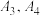 的前2项;
的前2项;
(2)记数列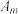 的第
的第 项为
项为 .求证:当
.求证:当 时,
时, ;
;
(3)若 ,求
,求 的值.
的值.
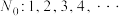 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列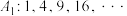 ,此时数列
,此时数列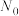 中剩下的项构成数列
中剩下的项构成数列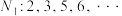 ;再将数列
;再将数列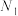 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列 ,剩下的项构成数列
,剩下的项构成数列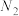 ;….如此操作下去,将数列
;….如此操作下去,将数列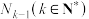 中项数为平方数的项依次选出构成数列
中项数为平方数的项依次选出构成数列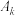 ,剩下的项构成数列
,剩下的项构成数列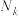 .
.(1)分别写出数列
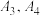 的前2项;
的前2项;(2)记数列
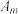 的第
的第 项为
项为 .求证:当
.求证:当 时,
时, ;
;(3)若
 ,求
,求 的值.
的值.
您最近一年使用:0次
2 . 激光的单光子通讯过程可用如下模型表述:发送方将信息加密后选择某种特定偏振状态的单光子进行发送,在信息传输过程中,若存在窃听者,由于密码本的缺失,窃听者不一定能正确解密并获取准确信息.
某次实验中,假设原始信息的单光子的偏振状态0,1,2,3等可能地出现,原始信息息的单光子的偏振状态与窃听者的解密信息的单光子的偏振状态有如下对应关系.
已知原始信息的任意一种单光子的偏振状态,对应的窃听者解密信息的单光子的偏振状态等可能地出现.
(1)若发送者发送的原始信息的单光子的偏振状态为1,求窃听者解密信息的单光子的偏振状态与原始信息的单光子的偏振状态相同的概率;
(2)若发送者连续三次发送的原始信息的单光子的偏振状态均为1,设窃听者解密信息的单光子的偏振状态为1的个数为 ,求
,求 的分布列和数学期望
的分布列和数学期望 ;
;
(3)已知发送者连续三次发送信息,窃听者解密信息的单光子的偏振状态均为1.设原始信息的单光子只有一种偏振状态的可能性为 ,有两种偏振状态的可能性为
,有两种偏振状态的可能性为 ,有三种偏振状态的可能性为
,有三种偏振状态的可能性为 ,试比较
,试比较 的大小关系.(结论不要求证明)
的大小关系.(结论不要求证明)
某次实验中,假设原始信息的单光子的偏振状态0,1,2,3等可能地出现,原始信息息的单光子的偏振状态与窃听者的解密信息的单光子的偏振状态有如下对应关系.
原始信息的单光子的偏振状态 | 0 | 1 | 2 | 3 |
解密信息的单光子的偏振状态 | 0,1,2 | 0,1,3 | 1,2,3 | 0,2,3 |
(1)若发送者发送的原始信息的单光子的偏振状态为1,求窃听者解密信息的单光子的偏振状态与原始信息的单光子的偏振状态相同的概率;
(2)若发送者连续三次发送的原始信息的单光子的偏振状态均为1,设窃听者解密信息的单光子的偏振状态为1的个数为
 ,求
,求 的分布列和数学期望
的分布列和数学期望 ;
;(3)已知发送者连续三次发送信息,窃听者解密信息的单光子的偏振状态均为1.设原始信息的单光子只有一种偏振状态的可能性为
 ,有两种偏振状态的可能性为
,有两种偏振状态的可能性为 ,有三种偏振状态的可能性为
,有三种偏振状态的可能性为 ,试比较
,试比较 的大小关系.(结论不要求证明)
的大小关系.(结论不要求证明)
您最近一年使用:0次
解题方法
3 . 某医学小组为了比较白鼠注射A,B两种药物后产生的皮肤疱疹的面积,选20只健康白鼠做试验.将这20只白鼠随机分成两组,每组10只,其中第1组注射药物A,第2组注射药物B.试验结果如下表所示.
(1)现分别从第1组,第2组的白鼠中各随机选取1只,求被选出的2只白鼠皮肤疱疹面积均小于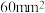 的概率;
的概率;
(2)从两组皮肤疱疹面积在 区间内的白鼠中随机选取3只抽血化验,求第2组中被抽中白鼠只数
区间内的白鼠中随机选取3只抽血化验,求第2组中被抽中白鼠只数 的分布列和数学期望
的分布列和数学期望 ;
;
(3)用“ ”表示第
”表示第 组白鼠注射药物后皮肤疱疹面积在
组白鼠注射药物后皮肤疱疹面积在 区间内,“
区间内,“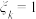 ”表示第
”表示第 组白鼠注射药物后皮肤疱疹面积在
组白鼠注射药物后皮肤疱疹面积在 区间内(
区间内( ),写出方差
),写出方差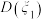 ,
,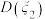 的大小关系.(结论不要求证明)
的大小关系.(结论不要求证明)
疱疹面积(单位: |
|
|
|
|
|
第1组(只) | 3 | 4 | 1 | 2 | 0 |
第2组(只) | 1 | 3 | 2 | 3 | 1 |
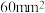 的概率;
的概率;(2)从两组皮肤疱疹面积在
 区间内的白鼠中随机选取3只抽血化验,求第2组中被抽中白鼠只数
区间内的白鼠中随机选取3只抽血化验,求第2组中被抽中白鼠只数 的分布列和数学期望
的分布列和数学期望 ;
;(3)用“
 ”表示第
”表示第 组白鼠注射药物后皮肤疱疹面积在
组白鼠注射药物后皮肤疱疹面积在 区间内,“
区间内,“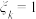 ”表示第
”表示第 组白鼠注射药物后皮肤疱疹面积在
组白鼠注射药物后皮肤疱疹面积在 区间内(
区间内( ),写出方差
),写出方差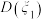 ,
,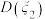 的大小关系.(结论不要求证明)
的大小关系.(结论不要求证明)
您最近一年使用:0次
名校
4 . 已知集合 (
( ,
, ),若存在数阵
),若存在数阵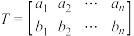 满足:
满足:
①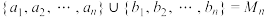 ;
;
② .
.
则称集合 为“好集合”,并称数阵
为“好集合”,并称数阵 为
为 的一个“好数阵”.
的一个“好数阵”.
(1)已知数阵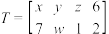 是
是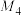 的一个“好数阵”,试写出
的一个“好数阵”,试写出 ,
, ,
, ,
, 的值;
的值;
(2)若集合 为“好集合”,证明:集合
为“好集合”,证明:集合 的“好数阵”必有偶数个;
的“好数阵”必有偶数个;
(3)判断 是否为“好集合”.若是,求出满足条件
是否为“好集合”.若是,求出满足条件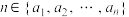 的所有“好数阵”;若不是,说明理由.
的所有“好数阵”;若不是,说明理由.
 (
( ,
, ),若存在数阵
),若存在数阵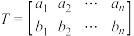 满足:
满足:①
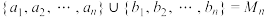 ;
;②
 .
.则称集合
 为“好集合”,并称数阵
为“好集合”,并称数阵 为
为 的一个“好数阵”.
的一个“好数阵”.(1)已知数阵
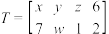 是
是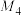 的一个“好数阵”,试写出
的一个“好数阵”,试写出 ,
, ,
, ,
, 的值;
的值;(2)若集合
 为“好集合”,证明:集合
为“好集合”,证明:集合 的“好数阵”必有偶数个;
的“好数阵”必有偶数个;(3)判断
 是否为“好集合”.若是,求出满足条件
是否为“好集合”.若是,求出满足条件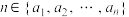 的所有“好数阵”;若不是,说明理由.
的所有“好数阵”;若不是,说明理由.
您最近一年使用:0次
2024-03-27更新
|
1028次组卷
|
4卷引用:北京市丰台区2023-2024学年高三下学期综合练习(一)数学试题
北京市丰台区2023-2024学年高三下学期综合练习(一)数学试题北京市第八十中学2023-2024学年高二下学期期中考试数学试题(已下线)压轴题01集合新定义、函数与导数13题型汇总 -1北京市日坛中学2023-2024学年高一下学期期中考试数学试题
5 . 对于数列 ,如果存在正整数
,如果存在正整数 ,使得对任意
,使得对任意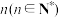 ,都有
,都有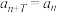 ,那么数列
,那么数列 就叫做周期数列,
就叫做周期数列, 叫做这个数列的周期.若周期数列
叫做这个数列的周期.若周期数列 ,
, 满足:存在正整数
满足:存在正整数 ,对每一个
,对每一个 ,都有
,都有 ,我们称数列
,我们称数列 和
和 为“同根数列”.
为“同根数列”.
(1)判断下列数列是否为周期数列.如果是,写出该数列的周期,如果不是,说明理由;
①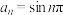 ;②
;②
(2)若 和
和 是“同根数列”,且周期的最小值分别是3和5,求证:
是“同根数列”,且周期的最小值分别是3和5,求证: ;
;
(3)若 和
和 是“同根数列”,且周期的最小值分别是
是“同根数列”,且周期的最小值分别是 和
和
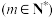 ,求
,求 的最大值.
的最大值.
 ,如果存在正整数
,如果存在正整数 ,使得对任意
,使得对任意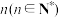 ,都有
,都有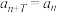 ,那么数列
,那么数列 就叫做周期数列,
就叫做周期数列, 叫做这个数列的周期.若周期数列
叫做这个数列的周期.若周期数列 ,
, 满足:存在正整数
满足:存在正整数 ,对每一个
,对每一个 ,都有
,都有 ,我们称数列
,我们称数列 和
和 为“同根数列”.
为“同根数列”.(1)判断下列数列是否为周期数列.如果是,写出该数列的周期,如果不是,说明理由;
①
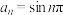 ;②
;②
(2)若
 和
和 是“同根数列”,且周期的最小值分别是3和5,求证:
是“同根数列”,且周期的最小值分别是3和5,求证: ;
;(3)若
 和
和 是“同根数列”,且周期的最小值分别是
是“同根数列”,且周期的最小值分别是 和
和
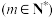 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
6 . 已知数表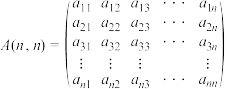 ,
,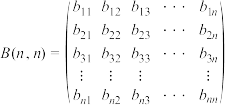 ,
, ,其中
,其中 ,
,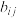 ,
,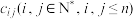 分别表示
分别表示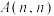 ,
,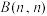 ,
, 中第
中第 行第
行第 列的数.若
列的数.若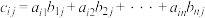 ,则称
,则称 是
是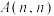 ,
,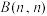 的生成数表.
的生成数表.
(1)若数表 ,
, ,且
,且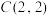 是
是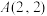 ,
,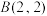 的生成数表,求
的生成数表,求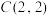 ;
;
(2)对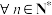 ,
, ,
,
数表 ,
, ,
, 与
与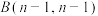 满足第i行第j列的数对应相同(
满足第i行第j列的数对应相同(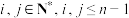 ).
). 是
是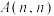 ,
, 的生成数表,且
的生成数表,且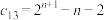 .
.
(ⅰ)求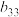 ,
,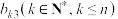 ;
;
(ⅱ)若 恒成立,求
恒成立,求 的最小值.
的最小值.
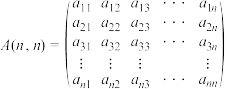 ,
,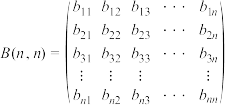 ,
, ,其中
,其中 ,
,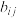 ,
,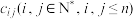 分别表示
分别表示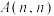 ,
,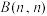 ,
, 中第
中第 行第
行第 列的数.若
列的数.若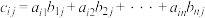 ,则称
,则称 是
是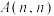 ,
,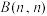 的生成数表.
的生成数表.(1)若数表
 ,
, ,且
,且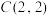 是
是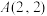 ,
,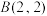 的生成数表,求
的生成数表,求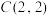 ;
;(2)对
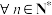 ,
, ,
,数表
 ,
, ,
, 与
与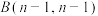 满足第i行第j列的数对应相同(
满足第i行第j列的数对应相同(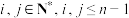 ).
). 是
是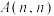 ,
, 的生成数表,且
的生成数表,且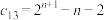 .
.(ⅰ)求
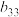 ,
,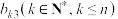 ;
;(ⅱ)若
 恒成立,求
恒成立,求 的最小值.
的最小值.
您最近一年使用:0次
解题方法
7 . 赵州桥,又名安济桥,位于河北省石家庄市赵县的洨河上,距今已有 多年的历史,是保存最完整的古代单孔敞肩石拱桥,其高超的技术水平和不朽的艺术价值,彰显了中国劳动人民的智慧和力量.2023年以来,中国文旅市场迎来强劲复苏,某地一旅游景点为吸引游客,参照赵州桥的样式在景区兴建圆拱桥,该圆拱桥的圆拱跨度为
多年的历史,是保存最完整的古代单孔敞肩石拱桥,其高超的技术水平和不朽的艺术价值,彰显了中国劳动人民的智慧和力量.2023年以来,中国文旅市场迎来强劲复苏,某地一旅游景点为吸引游客,参照赵州桥的样式在景区兴建圆拱桥,该圆拱桥的圆拱跨度为 ,拱高为
,拱高为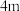 ,在该圆拱桥的示意图中建立如图所示的平面直角坐标系.
,在该圆拱桥的示意图中建立如图所示的平面直角坐标系.

(1)求这座圆拱桥的拱圆的方程;
(2)若该景区游船宽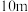 ,水面以上高
,水面以上高 ,试判断该景区游船能否从桥下通过,并说明理由.
,试判断该景区游船能否从桥下通过,并说明理由.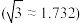
 多年的历史,是保存最完整的古代单孔敞肩石拱桥,其高超的技术水平和不朽的艺术价值,彰显了中国劳动人民的智慧和力量.2023年以来,中国文旅市场迎来强劲复苏,某地一旅游景点为吸引游客,参照赵州桥的样式在景区兴建圆拱桥,该圆拱桥的圆拱跨度为
多年的历史,是保存最完整的古代单孔敞肩石拱桥,其高超的技术水平和不朽的艺术价值,彰显了中国劳动人民的智慧和力量.2023年以来,中国文旅市场迎来强劲复苏,某地一旅游景点为吸引游客,参照赵州桥的样式在景区兴建圆拱桥,该圆拱桥的圆拱跨度为 ,拱高为
,拱高为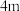 ,在该圆拱桥的示意图中建立如图所示的平面直角坐标系.
,在该圆拱桥的示意图中建立如图所示的平面直角坐标系.
(1)求这座圆拱桥的拱圆的方程;
(2)若该景区游船宽
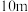 ,水面以上高
,水面以上高 ,试判断该景区游船能否从桥下通过,并说明理由.
,试判断该景区游船能否从桥下通过,并说明理由.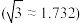
您最近一年使用:0次
2023-11-02更新
|
182次组卷
|
2卷引用:北京市丰台区2023-2024学年高二上学期期中练习数学试题(B)
8 . 设非零向量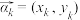 ,
,
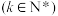 ,并定义
,并定义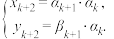
(1)若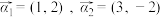 ,求
,求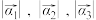 ;
;
(2)写出
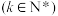 之间的等量关系,并证明;
之间的等量关系,并证明;
(3)若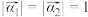 ,求证:集合
,求证:集合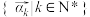 是有限集.
是有限集.
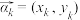 ,
,
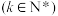 ,并定义
,并定义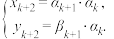
(1)若
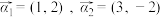 ,求
,求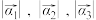 ;
;(2)写出

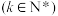 之间的等量关系,并证明;
之间的等量关系,并证明;(3)若
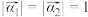 ,求证:集合
,求证:集合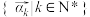 是有限集.
是有限集.
您最近一年使用:0次
2023-07-25更新
|
470次组卷
|
3卷引用:北京市丰台区2022-2023学年高一下学期期末考试数学试卷
北京市丰台区2022-2023学年高一下学期期末考试数学试卷(已下线)专题07 向量应用-《重难点题型·高分突破》(苏教版2019必修第二册)【北京专用】专题06平面向量(第二部分)-高一下学期名校期末好题汇编
名校
解题方法
9 . 在新高考背景下,北京高中学生需从思想政治、历史、地理、物理、化学、生物这6个科目中选择3个科目学习并参加相应的等级性考试.为提前了解学生的选科意愿,某校在期中考试之后,组织该校高一学生进行了模拟选科.为了解物理和其他科目组合的人数分布情况,某教师整理了该校高一(1)班和高一(2)班的相关数据,如下表:
其中高一(1)班共有40名学生,高一(2)班共有38名学生.假设所有学生的选择互不影响.
(1)从该校高一(1)班和高一(2)班所有学生中随机选取1人,求此人在模拟选科中选择了“物理+化学”的概率;
(2)从表中选择“物理+思想政治”的学生中随机选取2人参加座谈会,求这2人均来自高一(2)班的概率;
(3)该校在本学期期末考试之后组织高一学生进行了第二次选科,现从高一(1)班和高一(2)班各随机选取1人进行访谈,发现他们在第二次选科中都选择了“物理+历史”.根据这一结果,能否认为在第二次选科中选择“物理+历史”的人数发生了变化?说明理由.
| 物理+化学 | 物理+生物 | 物理+思想政治 | 物理+历史 | 物理+地理 | |
| 高一(1)班 | 10 | 6 | 2 | 1 | 7 |
| 高一(2)班. | 15 | 9 | 3 | 1 | 6 |
(1)从该校高一(1)班和高一(2)班所有学生中随机选取1人,求此人在模拟选科中选择了“物理+化学”的概率;
(2)从表中选择“物理+思想政治”的学生中随机选取2人参加座谈会,求这2人均来自高一(2)班的概率;
(3)该校在本学期期末考试之后组织高一学生进行了第二次选科,现从高一(1)班和高一(2)班各随机选取1人进行访谈,发现他们在第二次选科中都选择了“物理+历史”.根据这一结果,能否认为在第二次选科中选择“物理+历史”的人数发生了变化?说明理由.
您最近一年使用:0次
2023-07-25更新
|
488次组卷
|
4卷引用:北京市丰台区2022-2023学年高一下学期期末考试数学试卷
北京市丰台区2022-2023学年高一下学期期末考试数学试卷北京市海淀区北京交大附中2023-2024学年高一上学期12月月考数学试题(已下线)专题07 统计与概率4种常考题型归类-《期末真题分类汇编》(北京专用)【北京专用】专题16概率与统计-高一下学期名校期末好题汇编
名校
解题方法
10 . 2023年4月18日至27日,第二十届上海国际汽车工业展览会在上海国家会展中心举行,本次展会以“拥抱汽车行业新时代”为主题在今年的展会中,社会各界不仅能看到中国市场的强大活力,也能近距离了解各国产汽车自主品牌在推动“智电化”和可持续发展进程中取得的最新成果,为了解参观者对参展的某款国产新能源汽车的满意度,调研组从这款新能源汽车的参观者中随机抽取了50名参观者作为样本进行问卷测评,记录他们的评分,问卷满分100分.问卷结束后,将数据分成6组: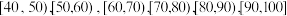 ,并整理得到如下频率分布直方图.
,并整理得到如下频率分布直方图.
(2)在样本中,从分数在60分以下的参观者中随机抽取3人,用X表示分数在 中的人数,求X的分布列及数学期望;
中的人数,求X的分布列及数学期望;
(3)在频率分布直方图中,用每一个小矩形底边中点的横坐标作为该组参观者评分的平均数,估计本次车展所有参观者对这款新能源汽车评分的平均数为m,若中位数的估计值为n,写出m与n的大小关系.(直接写出结果)
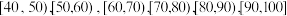 ,并整理得到如下频率分布直方图.
,并整理得到如下频率分布直方图.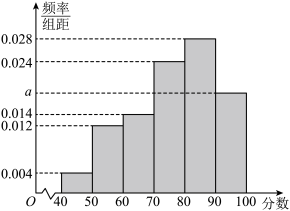
(2)在样本中,从分数在60分以下的参观者中随机抽取3人,用X表示分数在
 中的人数,求X的分布列及数学期望;
中的人数,求X的分布列及数学期望;(3)在频率分布直方图中,用每一个小矩形底边中点的横坐标作为该组参观者评分的平均数,估计本次车展所有参观者对这款新能源汽车评分的平均数为m,若中位数的估计值为n,写出m与n的大小关系.(直接写出结果)
您最近一年使用:0次
2023-07-10更新
|
413次组卷
|
5卷引用:北京市丰台区2022~2023学年高二下学期期末数学试题
北京市丰台区2022~2023学年高二下学期期末数学试题(已下线)专题11 离散型随机变量的数字特征(六大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)【北京专用】专题08概率与统计(第三部分)-高二上学期名校期末好题汇编北京市第六十六中学2023-2024学年高二下学期4月期中质量检测数学试题(已下线)专题06 离散型随机变量分布列及成对数据统计分析6种常考题型归类-1

 )
)