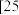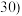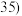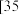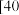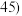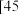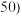名校
1 . 公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,发现了黄金分割约为0.618,这一数值也可以表示为m=2sin 18°,若m2+n=4,则 =( )
=( )
 =( )
=( )| A.8 | B.4 |
| C.2 | D.1 |
您最近一年使用:0次
2020-08-21更新
|
837次组卷
|
19卷引用:宁夏银川一中2018届高三第五次月考数学(理)试题
宁夏银川一中2018届高三第五次月考数学(理)试题湖北省重点高中联考协作体2017年秋季高三期中考试数学(文)试题湖北省重点高中联考协作体2017年秋季高三上学期期中考试数学(文)试题江西省临川二中、新余四中2018届高三1月联合考试数学(理)试题【全国百强校】河南省南阳市第一中学2018届高三第十九次考试数学(理)试题【全国百强校】吉林省实验中学2019届高三下学期第八次月考数学(理)试题吉林省吉林市实验中学2019届高三下学期第八次月考数学(文)试题【全国百强校】吉林省实验中学2019届高三下学期第八次月考数学(文)试题(已下线)专题4.2 简单的三角恒等变换-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破安徽省淮南市寿县第一中学2020届高三下学期最后一卷数学(理)试题安徽省淮南市寿县第一中学2020届高三下学期最后一卷数学(文)试题甘肃省金昌市永昌县第一高级中学2021届高三上学期期末数学(文)试题江西省分宜中学2020-2021学年高一(课改班)下学期第二次段考数学试题河南濮阳市华龙区高级中学2021-2022学年高三上学期开学考试数学文科试题湖南省衡阳市2022届高三下学期二模数学试题广东省茂名市2022届高三下学期调研(二)数学试题陕西省渭南市大荔县2021-2022学年高一下学期期末数学试题沪教版(2020) 必修第二册 新课改一课一练 第6章 6.2.3三角变换的应用【课堂练】 6.2.3.1 三角变换的应用(1)——角的变换 随堂练习-沪教版(2020)必修第二册 第6章 三角
名校
2 . 公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,发现0.618就是黄金分割,这是一个伟大的发现,这一数值也表示为 ,若
,若 ,则
,则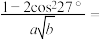
___________ .
 ,若
,若 ,则
,则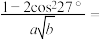
您最近一年使用:0次
2021-05-03更新
|
610次组卷
|
22卷引用:宁夏贺兰县景博中学2021届高三上学期统练(四)数学(理)试题
宁夏贺兰县景博中学2021届高三上学期统练(四)数学(理)试题湖北省“荆、荆、襄、宜四地七校考试联盟”2019年高三上学期10月月考数学(文)试题2020届湖北省部分重点中学高三上学期期末联考理科数学试题2020届内蒙古赤峰二中普通高等学校招生第三次统一模拟考试文科数学(已下线)冲刺卷07-决战2020年高考数学冲刺卷(山东专版)(已下线)第七篇三角函数03—2020年高考数学选填题专项测试(文理通用)内蒙古赤峰二中2020届普通高等学校招生第三次统一模拟考试理科数学试题(已下线)专题5.5+三角恒等变换-2020-2021学年高一数学尖子生同步培优题典(人教A版2019必修第一册)黑龙江省哈尔滨市第三中学校2020-2021学年高三上学期第二次验收考试理科数学试题黑龙江省哈尔滨市第三中学校2020-2021学年高三上学期第二次验收考试文科数学试题(已下线)练习9+三角恒等变换-2020-2021学年【补习教材·寒假作业】高一数学(人教A版2019)新疆乌鲁木齐市第七十中学2020-2021学年高一上学期期末考试数学试题四川省成都市石室中学2020-2021学年高三上学期一诊数学(文科)试题江苏省南京市第十四中学2020-2021学年高一下学期3月月考数学试题(已下线)专题06 三角恒等变换-备战2022年高考数学学霸纠错(全国通用)四川省叙永第一中学校2021-2022学年高三上学期第二次月考文科数学试题江苏省南京师范大学附属中学江宁分校2021-2022学年高一下学期期中数学试题河南省安阳市第一中学2023届高三第四次全真模拟数学试题江苏省扬州市江都区丁沟中学2022-2023学年高一下学期期中热身训练数学试题江苏省南通市如皋市2022-2023学年高三上学期期初模拟数学试题江苏省镇江市扬中市第二高级中学2023-2024学年高二上学期期初检测数学试题江苏省镇江市扬中市第二高级中学2023-2024学年高三上学期诊断性测试数学试题
名校
3 . 已知函数
(1)用五点作图在下面坐标系中做出上述函数在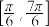 的图象.(请先列表,再描点,图中每个小矩形的宽度为
的图象.(请先列表,再描点,图中每个小矩形的宽度为
(2)请描述上述函数图象可以由函数y=sinx怎样变换而来?
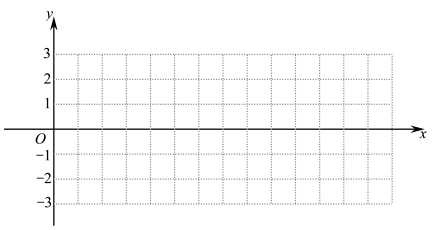

(1)用五点作图在下面坐标系中做出上述函数在
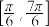 的图象.(请先列表,再描点,图中每个小矩形的宽度为
的图象.(请先列表,再描点,图中每个小矩形的宽度为
(2)请描述上述函数图象可以由函数y=sinx怎样变换而来?

您最近一年使用:0次
2019-07-01更新
|
1737次组卷
|
4卷引用:【全国百强校】宁夏石嘴山市第三中学2018-2019学年高一5月月考数学试题
2010·广东梅州·一模
名校
解题方法
4 . 某校从参加高一年级期中考试的学生中随机抽取 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段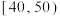 ,
, …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
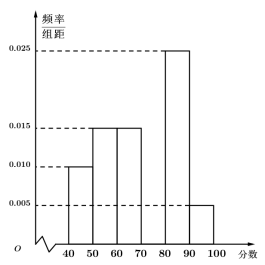
(1)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)用分层抽样的方法在分数段为 的学生中抽取一个容量为
的学生中抽取一个容量为 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取 人,求至多有
人,求至多有 人在分数段
人在分数段 的概率.
的概率.
 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在
 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;(2)用分层抽样的方法在分数段为
 的学生中抽取一个容量为
的学生中抽取一个容量为 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取 人,求至多有
人,求至多有 人在分数段
人在分数段 的概率.
的概率.
您最近一年使用:0次
2020-12-14更新
|
186次组卷
|
12卷引用:宁夏青铜峡市高级中学2020-2021学年高二12月月考数学(理)试题
宁夏青铜峡市高级中学2020-2021学年高二12月月考数学(理)试题(已下线)广东省梅州市2010年高三总复习质检试卷数学文科(已下线)2010年江苏省扬州中学高三第四次模拟考试数学试题(已下线)福建省泉州师院附属鹏峰中学2010届高三高考模拟试卷文科数学(已下线)2010年黑龙江省大庆市东风中学高二上学期期中考试数学卷(已下线)2011-2012学年福建省福州文博中学高一下学期期中考试文科数学试卷(已下线)2011—2012学年广东省佛山一中高一下学期期末数学试卷2015-2016学年广东省惠阳高级中学高二上学期期中考试理科数学试卷2016届山西省晋城市高三上学期期末理科数学试卷2016届山西省晋城市高三上学期期末文科数学试卷2015-2016学年福建省上杭县一中高二下周练文科数学试卷安徽省合肥市肥东县第二中学2021届高三下学期4月月考文科数学试题
名校
解题方法
5 . 某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动,组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后,学生会对问卷结果进行了统计,并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表:
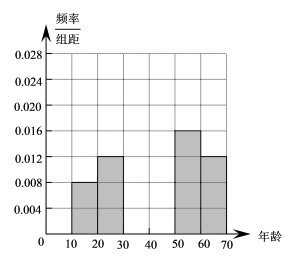
(1)求上表中的 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;
(2)在被调查的居民中,若从年龄在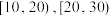 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
| 年龄(岁) | 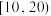 |  | 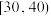 | 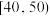 | 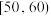 | 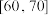 |
| 频数 |  |  | 14 | 12 | 8 | 6 |
| 知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |

(1)求上表中的
 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;(2)在被调查的居民中,若从年龄在
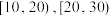 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
您最近一年使用:0次
2020-02-18更新
|
347次组卷
|
7卷引用:2015届四川省资阳市高三第三次模拟考试文科数学试卷
12-13高二上·黑龙江鹤岗·期末
名校
解题方法
6 . 某班同学利用国庆节进行社会实践,对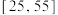 岁的人群随机抽取
岁的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
(1)补全频率分布直方图并求 、
、 、
、 的值;
的值;
(2)从年龄段在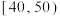 的“低碳族”中采用分层抽样法抽取
的“低碳族”中采用分层抽样法抽取 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取 人作为领队,求选取的
人作为领队,求选取的 名领队中恰有
名领队中恰有 人年龄在
人年龄在 岁的概率.
岁的概率.
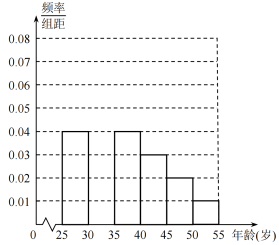
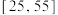 岁的人群随机抽取
岁的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
 、
、 、
、 的值;
的值;(2)从年龄段在
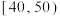 的“低碳族”中采用分层抽样法抽取
的“低碳族”中采用分层抽样法抽取 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取 人作为领队,求选取的
人作为领队,求选取的 名领队中恰有
名领队中恰有 人年龄在
人年龄在 岁的概率.
岁的概率.
您最近一年使用:0次
2017-10-07更新
|
729次组卷
|
26卷引用:2015-2016学年宁夏石嘴山三中高二上第一次月考数学试卷
2015-2016学年宁夏石嘴山三中高二上第一次月考数学试卷宁夏银川一中2017-2018学年高二上学期第一次月考数学试题(已下线)2011-2012学年黑龙江省鹤岗一中高二上学期期末考试理科数学(已下线)2013-2014学年四川资阳市高二第一学期期末考试文科数学试卷2014-2015学年海南文昌中学高一下学期期末理科数学试卷2016届吉林省实验中学高三上学期第一次模拟文科数学试卷2016-2017学年安徽寿县一中高二文上月考二数学试卷2016-2017学年河南省南阳市高一下学期期中质量评估数学试卷山东省枣庄市第八中学南校区2016-2017学年高一5月月考数学试题福建省2016届高三基地校总复习综合卷数学试题(厦门双十、南安一中、厦门海沧实验中学文科)人教A版高中数学必修三 模块综合评价数学试题广西南宁市第八中学2017-2018学年高一下学期期末考试数学试题江苏省南通市海安中学2016-2017学年高二上学期期中考试数学(理)试题人教B版(2019) 必修第二册 逆袭之路 第五章 统计与概率 整合提升西藏拉萨市第二高级中学2020届高三第六次月考数学试题(已下线)综合练习模拟卷05-2021年高考一轮数学(文)单元复习一遍过广东省台山市华侨中学2020-2021学年高二上学期第一次月考数学试题江西省宜春市奉新县第一中学2021-2022学年高二上学期第三次月考数学(文)试题西藏昌都市第一高级中学2021届高三上学期期末考试数学(文)试题(已下线)黄金卷06-【赢在高考·黄金20卷】备战2021年高考数学(文)全真模拟卷(新课标Ⅱ卷)四川省成都市蒲江县蒲江中学2020-2021学年高二下学期3月月考数学(理)试题(已下线)期末测试卷-2021-2022学年高一数学课后培优练(人教A版2019必修第二册)(已下线)专题10.2 概率 章末检测2(中)-【满分计划】2021-2022学年高一数学阶段性复习测试卷(人教A版2019必修第二册)河北省保定市第二十八中学2021-2022学年高一下学期第一次月考数学试题陕西省咸阳市高新一中2022-2023学年高二上学期期中理科数学试题(B卷)四川省绵阳市三台县2023-2024学年高二上学期期中教学质量调研数学测试题
名校
7 . 某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成 ,
,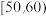 ,
, ,
,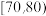 ,
, ,
, 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
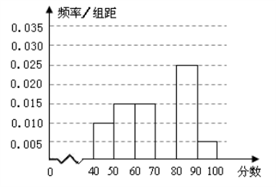
(1)求分数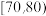 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
 ,
,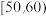 ,
, ,
,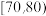 ,
, ,
, 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数
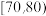 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
您最近一年使用:0次
2018-05-01更新
|
3483次组卷
|
14卷引用:宁夏青铜峡市高级中学(吴忠中学青铜峡分校)2019-2020学年高二下学期期中考试数学(理)试题
宁夏青铜峡市高级中学(吴忠中学青铜峡分校)2019-2020学年高二下学期期中考试数学(理)试题2016届黑龙江省牡丹江市一中高三上学期期末文科数学试卷2016-2017学年河南省南阳市第一中学高一下学期第一次月考(3月)数学试卷2016-2017学年辽宁省六校协作体高二下学期期初数学(理)试卷甘肃省西北师范大学附属中学2016届高三校内第一次诊断考试数学(文)试题【全国百强校】河南省南阳市第一中学2017-2018学年高一下学期第二次月考数学试题(已下线)2017-2018学年下学期期末复习备考之精准复习模拟题高一数学(A卷)(第01期)辽宁省沈阳市铁路实验中学2017-2018学年高二月考数学(文)试题山西省长治市第二中学2019-2020学年高一上学期期末数学试题甘肃省张掖市2018-2019学年高二下学期期末数学(文)试题甘肃省会宁县第一中学2019-2020学年高一下学期第一次月考数学试题(已下线)2020年秋季高二数学开学摸底考试卷(新教材人教A版)02(已下线)期末测试一(A卷基础卷)- 2020-2021学年高一数学必修第二册同步单元AB卷(新教材苏教版)(已下线)第15章 概率(综合测试卷)-2021-2022学年高一数学10分钟课前预习练(苏教版2019必修第二册)
名校
解题方法
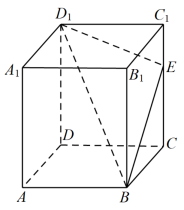
8 . 如图所示,在长方体 中,
中, ,点
,点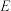 是棱
是棱 上的一个动点,若平面
上的一个动点,若平面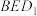 交棱
交棱 于点
于点 ,给出下列命题:
,给出下列命题:
①四棱锥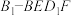 的体积恒为定值;
的体积恒为定值;
②存在点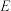 ,使得
,使得 平面
平面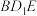 ;
;
③对于棱 上任意一点
上任意一点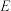 ,在棱
,在棱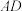 上均有相应的点
上均有相应的点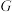 ,使得
,使得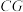
 平面
平面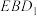 ;
;
④存在唯一的点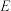 ,使得截面四边形
,使得截面四边形 的周长取得最小值.
的周长取得最小值.
其中真命题的是_____________ . (填写所有正确答案的序号)
 中,
中, ,点
,点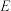 是棱
是棱 上的一个动点,若平面
上的一个动点,若平面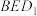 交棱
交棱 于点
于点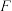 ,给出下列命题:
,给出下列命题:
①四棱锥
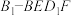 的体积恒为定值;
的体积恒为定值;②存在点
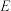 ,使得
,使得 平面
平面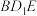 ;
;③对于棱
 上任意一点
上任意一点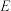 ,在棱
,在棱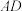 上均有相应的点
上均有相应的点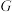 ,使得
,使得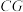
 平面
平面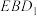 ;
;④存在唯一的点
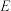 ,使得截面四边形
,使得截面四边形 的周长取得最小值.
的周长取得最小值.其中真命题的是
您最近一年使用:0次
2022-10-07更新
|
352次组卷
|
11卷引用:宁夏银川一中2021届高三第六次月考数学(理)试题
宁夏银川一中2021届高三第六次月考数学(理)试题宁夏银川一中2021届高三第六次月考数学(文)试题黑龙江省大庆市大庆实验中学2019-2020学年高三上学期期中数学(文)试题四川省内江市2019-2020学年高二上学期期末数学(理)试题湖南省邵阳市邵东县第十中学2020届高三下学期模拟考试数学(理)试题黑龙江省鹤岗市第一中学2020-2021学年高二10月月考数学(理)试题河北省张家口市第一中学2021届高三(衔接班)上学期期中数学试题(已下线)专题4.5 立体几何中探索性问题-玩转压轴题,进军满分之2021高考数学选择题填空题四川省成都市第八中学校2022-2023学年高三上学期第一次摸底考试文科数学试题河南省顶级名校2022-2023学年高三上学期12月摸底考试数学(文)试题(已下线)模块三 专题3 小题满分挑战练(3)(人教B)
名校
9 . 在某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是__________ (填写序号).
①平均数 ; ②标准差
; ②标准差 ; ③平均数
; ③平均数 且极差小于或等于2;
且极差小于或等于2;
④平均数 且标准差
且标准差 ; ⑤众数等于1且极差小于或等于4.
; ⑤众数等于1且极差小于或等于4.
①平均数
 ; ②标准差
; ②标准差 ; ③平均数
; ③平均数 且极差小于或等于2;
且极差小于或等于2;④平均数
 且标准差
且标准差 ; ⑤众数等于1且极差小于或等于4.
; ⑤众数等于1且极差小于或等于4.
您最近一年使用:0次
2022-03-28更新
|
303次组卷
|
10卷引用:2016-2017学年河南省南阳市高一下学期期中质量评估数学试卷
2016-2017学年河南省南阳市高一下学期期中质量评估数学试卷内蒙古赤峰二中2016-2017学年高二下学期第二次月考数学(理)试题2020届天津市第四中学高三年高考模拟(4月份)数学试题湖南省邵阳市邵东市第三中学2020-2021学年高一上学期第二次月考数学试题宁夏银川市第二中学2021-2022学年高一上学期期末考试数学试题江西省南昌市八一中学、洪都中学、十七中三校2021届高三上学期期末联考数学(文)试题江西省南昌市八一中学、洪都中学、十七中三校2021届高三上学期期末联考数学(理)试题河南省信阳高级中学2020-2021学年高二下学期回顾测试数学(理)试题(已下线)考点50 统计-备战2021年高考数学经典小题考前必刷(新高考地区专用)湖北省襄阳市第五中学2021-2022学年高一下学期6月月考数学试题
名校
10 . 市教育部门为研究高中学生的身体素质与课外体育锻炼时间的关系,对该市某校 名高中学生的课外体育锻炼平均每天锻炼的时间进行了调查,数据如下表:
名高中学生的课外体育锻炼平均每天锻炼的时间进行了调查,数据如下表:
将学生日均课外体育锻炼时间在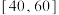 内的学生评价为“课外体育达标”.
内的学生评价为“课外体育达标”.
(1)请根据上述表格中的统计数据填写下面 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过 的前提下认为“课外体育达标”与性别有关;
的前提下认为“课外体育达标”与性别有关;
(2)从上述课外体育不达标的学生中,按性别用分层抽样的方法抽取 名学生,再从这
名学生,再从这 名学生中随机抽取
名学生中随机抽取 人了解他们锻炼时间偏少的原因,记所抽取的
人了解他们锻炼时间偏少的原因,记所抽取的 人中男生的人数为随机变量
人中男生的人数为随机变量 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(3)将上述调查所得到的概率视为概率来估计全市的情况,现在从该市所有高中学生中抽取 名学生,求其中恰好有
名学生,求其中恰好有 名学生课外体育达标的概率.
名学生课外体育达标的概率.
附:参考公式及临界值表: ,其中
,其中 .
.
 名高中学生的课外体育锻炼平均每天锻炼的时间进行了调查,数据如下表:
名高中学生的课外体育锻炼平均每天锻炼的时间进行了调查,数据如下表:| 平均每天锻炼的时间(分钟) | 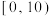 | 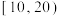 | 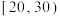 | 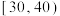 | 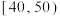 |  |
| 总人数 |  |  |  |  |  |  |
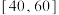 内的学生评价为“课外体育达标”.
内的学生评价为“课外体育达标”.(1)请根据上述表格中的统计数据填写下面
 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过 的前提下认为“课外体育达标”与性别有关;
的前提下认为“课外体育达标”与性别有关;| 课外体育不达标 | 课外体育达标 | 总计 | |
| 男 | |||
| 女 |  | 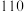 | |
| 总计 |
 名学生,再从这
名学生,再从这 名学生中随机抽取
名学生中随机抽取 人了解他们锻炼时间偏少的原因,记所抽取的
人了解他们锻炼时间偏少的原因,记所抽取的 人中男生的人数为随机变量
人中男生的人数为随机变量 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(3)将上述调查所得到的概率视为概率来估计全市的情况,现在从该市所有高中学生中抽取
 名学生,求其中恰好有
名学生,求其中恰好有 名学生课外体育达标的概率.
名学生课外体育达标的概率.附:参考公式及临界值表:
 ,其中
,其中 .
. ( ( ) ) |  |  |  |  |  |
 |  |  |  |  |  |
您最近一年使用:0次
2021-07-19更新
|
424次组卷
|
4卷引用:湖南省湘东六校2018-2019学年高三上学期12月联考理科数学试题