名校
1 . 意大利数学家斐波那契以兔子繁殖数量为例,引入数列:1,1,2,3,5,8,该数列从第三项起,每一项都等于前两项之和,即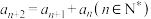 ,故此数列称为斐波那契数列,又称为“兔子数列”,其通项公式为
,故此数列称为斐波那契数列,又称为“兔子数列”,其通项公式为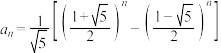 ,设
,设 是不等式
是不等式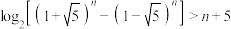 的正整数解,则
的正整数解,则 的最小值为( )
的最小值为( )
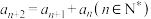 ,故此数列称为斐波那契数列,又称为“兔子数列”,其通项公式为
,故此数列称为斐波那契数列,又称为“兔子数列”,其通项公式为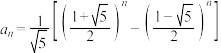 ,设
,设 是不等式
是不等式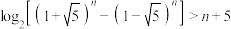 的正整数解,则
的正整数解,则 的最小值为( )
的最小值为( )| A.7 | B.8 | C.9 | D.10 |
您最近一年使用:0次
解题方法
2 . 随着经济发展,越来越多的家庭开始关注到家庭成员的关系,一个以“从心定义家庭关系”为主题的应用心理学的学习平台,从建立起,得到了很多人的关注,也有越来越多的人成为平台的会员,主动在平台上进行学习.已知前四年,平台会员的个数如图所示:

(1)依据图中数据,从下列三种模型中选择一个恰当的模型估算建立平台 年后平台会员人数
年后平台会员人数 (千人),并求出你选择模型的解析式;
(千人),并求出你选择模型的解析式;
① ,②
,② 且
且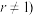 ,③
,③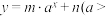 0且
0且 ).
).
(2)为控制平台会员人数盲目扩大,平台规定无论怎样发展,会员人数不得超过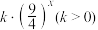 千人,请依据(1)中你选择的函数模型求
千人,请依据(1)中你选择的函数模型求 的最小值.
的最小值.

(1)依据图中数据,从下列三种模型中选择一个恰当的模型估算建立平台
 年后平台会员人数
年后平台会员人数 (千人),并求出你选择模型的解析式;
(千人),并求出你选择模型的解析式;①
 ,②
,② 且
且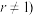 ,③
,③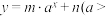 0且
0且 ).
).(2)为控制平台会员人数盲目扩大,平台规定无论怎样发展,会员人数不得超过
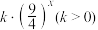 千人,请依据(1)中你选择的函数模型求
千人,请依据(1)中你选择的函数模型求 的最小值.
的最小值.
您最近一年使用:0次
名校
解题方法
3 . 高斯是德国数学家、天文学家和物理学家,被誉为历史上伟大的数学家之一,和阿基米德、牛顿并列,同享盛名.用他名字命名的高斯函数也称取整函数,记作 ,是指不超过实数
,是指不超过实数 的最大整数,例如
的最大整数,例如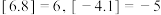 ,该函数被广泛应用于数论、函数绘图和计算机领域.若函数
,该函数被广泛应用于数论、函数绘图和计算机领域.若函数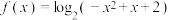 ,则当
,则当 时,
时,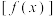 的值域为( )
的值域为( )
 ,是指不超过实数
,是指不超过实数 的最大整数,例如
的最大整数,例如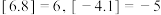 ,该函数被广泛应用于数论、函数绘图和计算机领域.若函数
,该函数被广泛应用于数论、函数绘图和计算机领域.若函数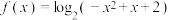 ,则当
,则当 时,
时,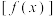 的值域为( )
的值域为( )A. | B.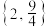 | C.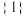 | D. |
您最近一年使用:0次
2024-01-16更新
|
529次组卷
|
4卷引用:河北省2024届高三上学期大数据应用调研联合测评数学试题
河北省2024届高三上学期大数据应用调研联合测评数学试题广东省东莞市东华高级中学2024届高三上学期第二次调研数学试题河北省石家庄市十八中2024届高三上学期1月联考数学试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练
4 . 在财务审计中,我们可以用“本•福特定律”来检验数据是否造假.本福特定律指出,在一组没有人为编造的自然生成的数据(均为正实数)中,首位非零的数字是 这九个事件不是等可能的.具体来说,随机变量
这九个事件不是等可能的.具体来说,随机变量 是一组没有人为编造的首位非零数字,则
是一组没有人为编造的首位非零数字,则 .则根据本•福特定律,首位非零数字是1与首位非零数字是8的概率之比约为( )(保留至整数,参考数据:
.则根据本•福特定律,首位非零数字是1与首位非零数字是8的概率之比约为( )(保留至整数,参考数据: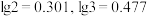 ).
).
 这九个事件不是等可能的.具体来说,随机变量
这九个事件不是等可能的.具体来说,随机变量 是一组没有人为编造的首位非零数字,则
是一组没有人为编造的首位非零数字,则 .则根据本•福特定律,首位非零数字是1与首位非零数字是8的概率之比约为( )(保留至整数,参考数据:
.则根据本•福特定律,首位非零数字是1与首位非零数字是8的概率之比约为( )(保留至整数,参考数据: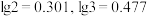 ).
).| A.4 | B.6 | C.7 | D.8 |
您最近一年使用:0次
2024-01-16更新
|
574次组卷
|
4卷引用:辽宁省大连市2024届高三上学期双基测试数学试题
辽宁省大连市2024届高三上学期双基测试数学试题辽宁省沈阳市、大连市2023-2024学年高二上学期教学联盟大联考数学试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练(已下线)思想02 运用数形结合的思想方法解题(4大核心考点)(讲义)
解题方法
5 . 意大利画家达芬奇在创作《抱银貂的女子》时思考了一个问题:画中女子佩戴着一条长长的项链,项链所形成的曲线是什么?这就是著名的“悬链线问题”.选择适当的坐标系后,悬链线的方程是双曲余弦函数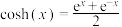 ,类似的有双曲正弦函数
,类似的有双曲正弦函数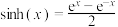 .则
.则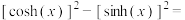
________ ,设函数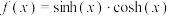 ,则不等式
,则不等式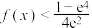 的解集为
的解集为________ .
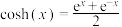 ,类似的有双曲正弦函数
,类似的有双曲正弦函数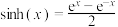 .则
.则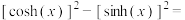
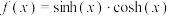 ,则不等式
,则不等式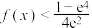 的解集为
的解集为
您最近一年使用:0次
名校
6 . 意大利数学家斐波那契以兔子繁殖数量为例,引入数列:1,1,2,3,5,8,该数列从第三项起,每一项都等于前两项之和,即 ,故此数列称为斐波那契数列,又称为“兔子数列”,其通项公式为
,故此数列称为斐波那契数列,又称为“兔子数列”,其通项公式为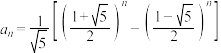 ,设
,设 是不等式
是不等式 的正整数解,则
的正整数解,则 的最小值为( )
的最小值为( )
 ,故此数列称为斐波那契数列,又称为“兔子数列”,其通项公式为
,故此数列称为斐波那契数列,又称为“兔子数列”,其通项公式为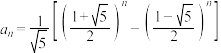 ,设
,设 是不等式
是不等式 的正整数解,则
的正整数解,则 的最小值为( )
的最小值为( )| A.6 | B.7 | C.8 | D.9 |
您最近一年使用:0次
2024-01-12更新
|
779次组卷
|
6卷引用:河北省廊坊市部分高中2024届高三上学期期末数学试题
河北省廊坊市部分高中2024届高三上学期期末数学试题(已下线)考点15 数列中的数学文化 2024届高考数学考点总动员【练】广东省汕头市金山中学2024届高三上学期第一次模拟考试数学试题(已下线)第1讲:数列的函数性质应用【练】(已下线)压轴题数列新定义题(九省联考第19题模式)练(已下线)模块三 失分陷阱2 不会从情境中抽出数列模型或关系
名校
7 . 意大利画家达·芬奇提出:固定项链的两端,使其在重力的作用下自然下垂,那么项链所形成的曲线是什么?这就是著名的“悬链线问题”,其中双曲余弦函数就是一种特殊的悬链线函数,其函数表达式为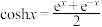 ,相应的双曲正弦函数的表达式为
,相应的双曲正弦函数的表达式为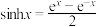 .设函数
.设函数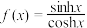 ,则( )
,则( )
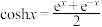 ,相应的双曲正弦函数的表达式为
,相应的双曲正弦函数的表达式为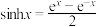 .设函数
.设函数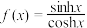 ,则( )
,则( )A.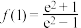 |
B.函数 在其定义域上是增函数 在其定义域上是增函数 |
C.若实数 满足不等式 满足不等式 ,则 ,则 的取值范围是 的取值范围是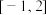 |
D.函数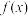 的值域为 的值域为 |
您最近一年使用:0次
2024-01-12更新
|
264次组卷
|
2卷引用:吉林省吉林市普通高中2023-2024学年高一上学期期末调研测试数学试题
名校
8 . 茶,是中华民族的举国之饮,它发乎神农,闻于鲁周公,兴于唐朝,盛在宋代,如今已成了风靡世界的三大无酒精饮料(茶叶、咖啡和可可)之一,并将成为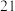 世纪的饮料大王.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.把物体放在冷空气中冷却,如果物体原来的温度是
世纪的饮料大王.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.把物体放在冷空气中冷却,如果物体原来的温度是
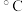 ,空气温度是
,空气温度是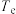
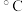 ,那么
,那么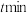 后物体的温度
后物体的温度 (单位:
(单位: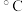 )可由公式
)可由公式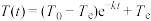 求得,其中
求得,其中 是一个随着物体与空气的接触情况而定的常数.现有某种刚泡好的普洱茶,茶水温度是
是一个随着物体与空气的接触情况而定的常数.现有某种刚泡好的普洱茶,茶水温度是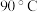 ,放在室温
,放在室温 的环境中自然冷却,
的环境中自然冷却,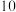 分钟后茶水的温度是
分钟后茶水的温度是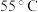 .
.
(1)求 的值;
的值;
(2)经验表明,当室温为 摄氏度时,该种普洱茶用
摄氏度时,该种普洱茶用 的水泡制,自然冷却至
的水泡制,自然冷却至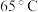 时饮用,可以产生最佳口感,那么,刚泡好的茶水在室温为
时饮用,可以产生最佳口感,那么,刚泡好的茶水在室温为 时自然冷却大约需要放置多长时间才能达到最佳饮用口感?(结果精确到
时自然冷却大约需要放置多长时间才能达到最佳饮用口感?(结果精确到 )
)
(附:参考值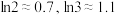 )
)
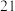 世纪的饮料大王.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.把物体放在冷空气中冷却,如果物体原来的温度是
世纪的饮料大王.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.把物体放在冷空气中冷却,如果物体原来的温度是
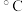 ,空气温度是
,空气温度是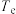
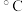 ,那么
,那么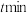 后物体的温度
后物体的温度 (单位:
(单位: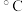 )可由公式
)可由公式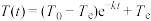 求得,其中
求得,其中 是一个随着物体与空气的接触情况而定的常数.现有某种刚泡好的普洱茶,茶水温度是
是一个随着物体与空气的接触情况而定的常数.现有某种刚泡好的普洱茶,茶水温度是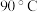 ,放在室温
,放在室温 的环境中自然冷却,
的环境中自然冷却,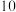 分钟后茶水的温度是
分钟后茶水的温度是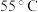 .
.(1)求
 的值;
的值;(2)经验表明,当室温为
 摄氏度时,该种普洱茶用
摄氏度时,该种普洱茶用 的水泡制,自然冷却至
的水泡制,自然冷却至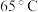 时饮用,可以产生最佳口感,那么,刚泡好的茶水在室温为
时饮用,可以产生最佳口感,那么,刚泡好的茶水在室温为 时自然冷却大约需要放置多长时间才能达到最佳饮用口感?(结果精确到
时自然冷却大约需要放置多长时间才能达到最佳饮用口感?(结果精确到 )
)(附:参考值
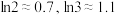 )
)
您最近一年使用:0次
2024-01-12更新
|
283次组卷
|
2卷引用:吉林省吉林市普通高中2023-2024学年高一上学期期末调研测试数学试题
解题方法
9 . 如图,沈阳东塔桥是沈阳唯一一座“双塔钢结构自锚式悬索桥”,悬索的形状是平面几何中的悬链线,悬链线方程为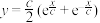 (
( 为参数,
为参数,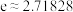 ),当
),当 时,该方程就是双曲余弦函数
时,该方程就是双曲余弦函数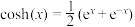 ,类似的有双曲正弦函数
,类似的有双曲正弦函数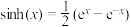 .
. ;
;
(2)当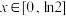 时,求
时,求 的最小值
的最小值 ;
;
(3)设 ,证明:
,证明: 有唯一的正零点
有唯一的正零点 ,并比较
,并比较 和
和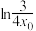 的大小.
的大小.
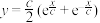 (
( 为参数,
为参数,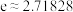 ),当
),当 时,该方程就是双曲余弦函数
时,该方程就是双曲余弦函数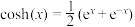 ,类似的有双曲正弦函数
,类似的有双曲正弦函数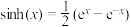 .
.
 ;
;(2)当
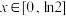 时,求
时,求 的最小值
的最小值 ;
;(3)设
 ,证明:
,证明: 有唯一的正零点
有唯一的正零点 ,并比较
,并比较 和
和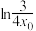 的大小.
的大小.
您最近一年使用:0次
解题方法
10 . 在沪教版教材必修第一册第四章的章首语中有这样一段话:“通过固定等式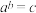 中的三个量
中的三个量 中的一个量,研究另两个量的相互关系和变化规律,定义三种基本而应用广泛的函数——幂函数、指数函数和对数函数”.若令
中的一个量,研究另两个量的相互关系和变化规律,定义三种基本而应用广泛的函数——幂函数、指数函数和对数函数”.若令 (
( 是自然对数的底数),将
是自然对数的底数),将 视为自变量
视为自变量 ,则
,则 为
为 的函数,记作
的函数,记作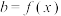 ,若不等式
,若不等式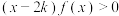 对任意的
对任意的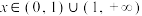 恒成立,则实数
恒成立,则实数 的值为
的值为__________ .
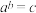 中的三个量
中的三个量 中的一个量,研究另两个量的相互关系和变化规律,定义三种基本而应用广泛的函数——幂函数、指数函数和对数函数”.若令
中的一个量,研究另两个量的相互关系和变化规律,定义三种基本而应用广泛的函数——幂函数、指数函数和对数函数”.若令 (
( 是自然对数的底数),将
是自然对数的底数),将 视为自变量
视为自变量 ,则
,则 为
为 的函数,记作
的函数,记作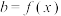 ,若不等式
,若不等式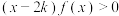 对任意的
对任意的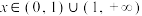 恒成立,则实数
恒成立,则实数 的值为
的值为
您最近一年使用:0次



